Problem A
税率変更
消費税は売価に比例した定率を課す税である.
私たちの店では,以下のルールによって税込価格を計算する.
- 消費税率が x% のとき,
税抜価格が p 円である商品の税込価格は,
p (100+x) / 100 円を小数点以下切り捨てたものである. - 複数の商品についてまとめて支払う際の税込合計価格は,
個々の商品の税込価格の合計額とする.
消費税率はしょっちゅう変更される.
私たちの店の会計係は,
「税込合計価格が同じだった2商品の組が,消費税率の変更後に異なる税込合計価格になりうる」
ことに気付いた.
たとえば,
消費税率が 5% から 8% に上がると,引上げ前に税込合計価格 105 円であった2商品の税込合計金額は,
下表に示すとおり 107 円,108 円,109 円のいずれかとなる.
| 2商品の税抜価格 | 消費税率 5% 時の税込価格 | 消費税率 8% 時の税込価格 |
|---|---|---|
| 20, 80 | 21 + 84 = 105 | 21 + 86 = 107 |
| 2, 99 | 2 + 103 = 105 | 2 + 106 = 108 |
| 13, 88 | 13 + 92 = 105 | 14 + 95 = 109 |
会計係が消費税率変更の影響を調査している.
2つの商品の消費税率変更前の税込合計価格を元に,
新消費税率での税込合計価格が最大いくらになるかを計算するプログラムを作って欲しい.
Input
入力は複数のデータセットからなる.
各データセットは1行からなり,
その行は空白で区切られた3つの整数 x, y, s からなる.
x は変更前の消費税率(パーセント),
y は変更後の消費税率(パーセント),
s は消費税率変更前の 2 商品の税込合計価格である.
これらの整数は,0 < x < 100, 0 < y < 100,
10 < s < 1000,x ≠ y を満たす.
商品の税抜価格として 1 円から s-1 円のすべてを考慮に入れよ.
入力の終わりは,空白で区切られた3つのゼロからなる行によって示される.
Output
各データセットについて,
消費税率が y% になったときにとりうる税込合計価格の最大値を1行で出力せよ.
Sample Input
5 8 105 8 5 105 1 2 24 99 98 24 12 13 26 1 22 23 1 13 201 13 16 112 2 24 50 1 82 61 1 84 125 1 99 999 99 1 999 98 99 999 1 99 11 99 1 12 0 0 0
Output for the Sample Input
109 103 24 24 26 27 225 116 62 111 230 1972 508 1004 20 7
ヒント
以下の表に,
消費税率変更後に税込価格が最大となる税抜価格の組み合わせ例を,
サンプル入力のデータセットごとに1つずつ示す.
| データセット | 税抜価格 | 消費税率 y% 時の税込価格 |
|---|---|---|
| 5 8 105 | 13, 88 | 14 + 95 = 109 |
| 8 5 105 | 12, 87 | 12 + 91 = 103 |
| 1 2 24 | 1, 23 | 1 + 23 = 24 |
| 99 98 24 | 1, 12 | 1 + 23 = 24 |
| 12 13 26 | 1, 23 | 1 + 25 = 26 |
| 1 22 23 | 1, 22 | 1 + 26 = 27 |
| 1 13 201 | 1,199 | 1 +224 = 225 |
| 13 16 112 | 25, 75 | 29 + 87 = 116 |
| 2 24 50 | 25, 25 | 31 + 31 = 62 |
| 1 82 61 | 11, 50 | 20 + 91 = 111 |
| 1 84 125 | 50, 75 | 92 +138 = 230 |
| 1 99 999 | 92,899 | 183+1789 =1972 |
| 99 1 999 | 1,502 | 1 +507 = 508 |
| 98 99 999 | 5,500 | 9 +995 =1004 |
| 1 99 11 | 1, 10 | 1 + 19 = 20 |
| 99 1 12 | 1, 6 | 1 + 6 = 7 |
Problem B
連鎖消滅パズル
皆さんはあるパズルに取り組んでいる.
このパズルには,下図に示すような,H 行,5 列のセルからなる,直立した盤を使う.
各セルには1から9までの数字が1つ刻まれた石が配置されている.
3個以上の水平に隣り合うセルに同じ数字を彫った石があれば,これらの石は消滅する.
石が消滅したセルの上方のセルに石があれば,それらは順次落ちて空きを埋める.
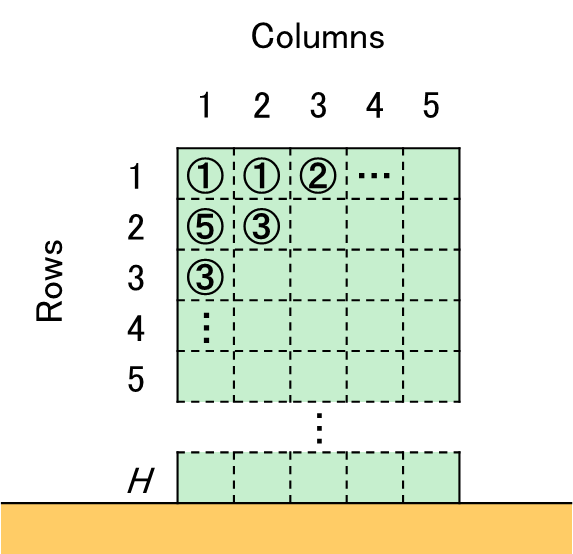
パズルは以下のステップに従って進行する.
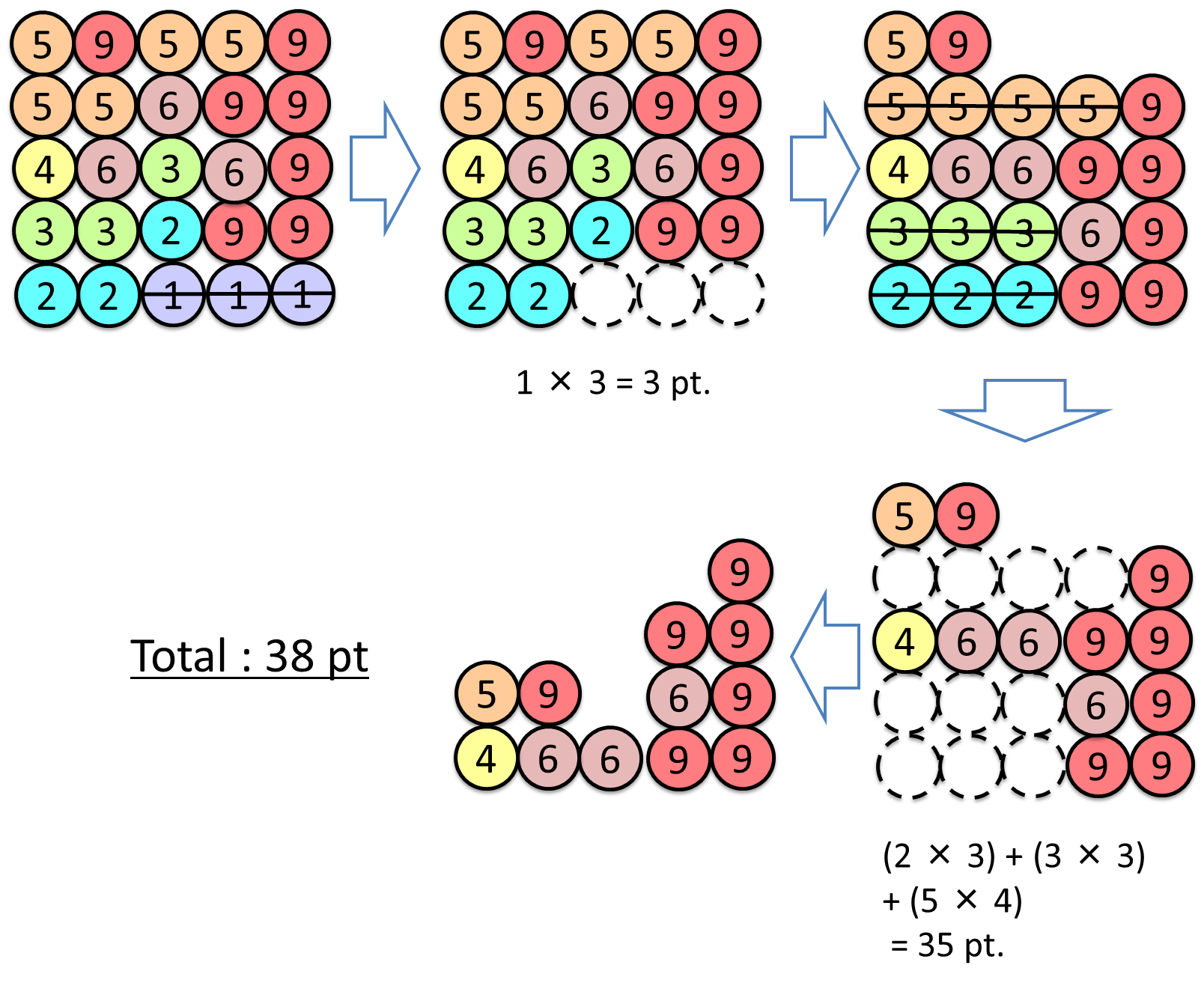
- 3個以上の水平に隣り合うセルに同じ数字を彫った石があれば,これらの石は消滅する.こうした石群の消滅はすべて同時に起きる.
- 石が消滅したセルの上方のセルに石があれば,空きを埋めるように石が落下する.
- すべての石の落下完了後に,消滅の条件を満たすようになった石群があれば,ステップ1に戻って繰り返す.
このパズルのスコアは消滅した石の数字の合計である.
与えられた石の配置で獲得できるスコアを計算するプログラムを作れ.
Input
入力は複数のデータセットからなる.
各データセットは以下の形をしている
盤面の高さ H
行1の石の並び
行2の石の並び
…
行 H の石の並び
各データセットの1行目には,パズル盤の高さ( H )が指定されている(1 ≤ H ≤ 10).
残りの H 行には,各行の石の並びが上から下の順に指定されている.
石の並びは空白で区切った1から9までの5個の数字で与えられる.
数字はその順に当該の行の5個の石に彫られている.
入力の終わりは,1つのゼロからなる行で示す.
Output
各データセットに対して,スコアを求め1行に出力せよ.
各出力行はスコアを表す数字以外を含んではならない.
Sample Input
1 6 9 9 9 9 5 5 9 5 5 9 5 5 6 9 9 4 6 3 6 9 3 3 2 9 9 2 2 1 1 1 10 3 5 6 5 6 2 2 2 8 3 6 2 5 9 2 7 7 7 6 1 4 6 6 4 9 8 9 1 1 8 5 6 1 8 1 6 8 2 1 2 9 6 3 3 5 5 3 8 8 8 5 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 3 2 2 8 7 4 6 5 7 7 7 8 8 9 9 9 0
Output for the Sample Input
36 38 99 0 72
(End of Problem B) A B C D E F G
Problem C
バンパイア
C氏はバンパイアである.太陽の光を直接浴びると灰になってしまうのだが,昨夜,
不死者と死人のプログラマー同好会(ICPC)に参加していたら,帰宅が夜明けに近い時間になってしまった.
幸いなことに,C氏の自宅周辺には背の高いビルが多く,太陽の光がビルにさえぎられている間は安全に動き回ることができる.
いま太陽の上端が地平線にかかったところだが,C氏が安全に棺桶に入るまでにあと何秒の猶予があるだろうか?
簡単のため,東の空をx 軸が水平,y 軸が垂直方向の2次元
x-y 平面で表し,建物のシルエットはこの平面上の長方形,
太陽は円で近似するものとする.
x 軸が地平線を表す.時刻をt で表し,現在の時刻をt=0とする.太陽は半径 r で,時刻 t=0 における中心は
(0, -r) にあり,x-y平面上を 毎秒 (0, 1) の等速直線運動を
しているものとする.
太陽(境界線を含む)の全体が,シルエット(境界線を含む)および地平線以下の領域(y ≤ 0)の和集合に含まれていれば,太陽の光はさえぎられている.
太陽の光がさえぎられている最後の瞬間の時刻を計算するプログラムを書け.
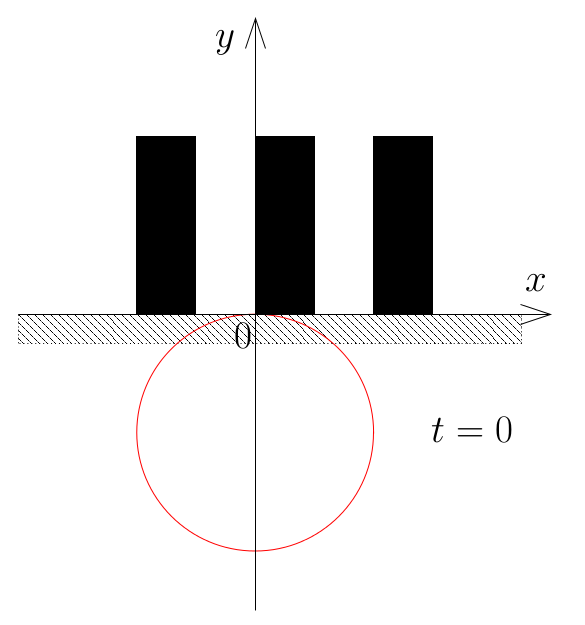
次の図は,後に示す Sample Input 中の最初のデータセットに対応するシルエットの配置と
太陽の光がさえぎられている最後の瞬間 (t=0) を示す.
このように,時刻 t=0 が太陽の光がさえぎられている最後の瞬間であることもありうる.
シルエット同士が辺で接する場合も,隙間は無く太陽の光はさえぎられる.
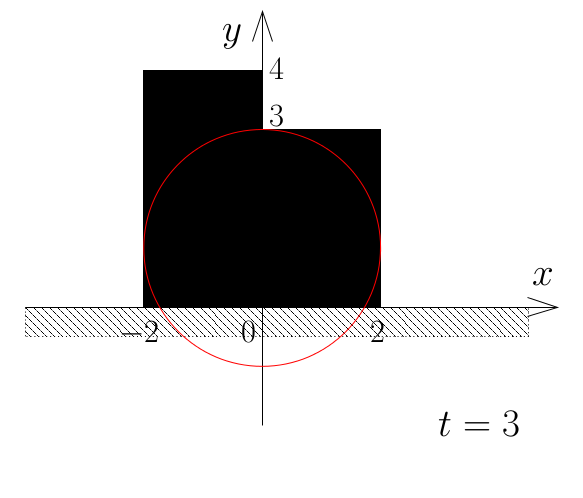
下の図は,Sample Input の 2番目のデータセットに対応するシルエットの配置と,
太陽の光がさえぎられている最後の瞬間 (t=3) を示す.
太陽の半径が 2で, -2 ≤ x ≤ 0 に高さ 4,0 ≤ x ≤ 2
に高さ 3 の2つのシルエットが与えられた例である.
Input
入力は複数のデータセットからなる.各データセットの最初の行は,
空白で区切られた2つの整数 r と n からなる.
r は太陽の半径を表し,n は建物のシルエットの個数を表す.
(1 ≤ r ≤ 20, 0 ≤ n ≤ 20)
続く n行のそれぞれは,空白で区切られた 3つの整数 xli,
xri, hi (1 ≤ i ≤ n)
からなる.
この 3つの整数は,建物のシルエットの長方形を指定する.シルエットの長方
形は地平線に平行で,左右の辺はx = xli と
x = xri に一致し,上辺は y =
hi に,下辺は地平線に一致している.
(-20 ≤ xli < xri ≤ 20,
0 < hi ≤ 20)
入力の終わりは空白で区切られた 2つのゼロからなる行で表される.
こうして与えられる建物のシルエットは重なっているかもしれないので注意すること.
Output
答えには 0.001 を越える誤差があってはならない.
それ以外の余計な文字を出力してはならない.
Sample Input
2 3 -2 -1 3 0 1 3 2 3 3 2 2 -2 0 4 0 2 3 2 6 -3 3 1 -2 3 2 -1 3 3 0 3 4 1 3 5 2 3 6 2 6 -3 3 1 -3 2 2 -3 1 3 -3 0 4 -3 -1 5 -3 -2 6 0 0
Output for the Sample Input
0.0000 3.0000 2.2679 2.2679
(End of Problem C) A B C D E F G
Problem D
暗号化システム
あるプログラマーが新しい暗号化システムを開発した.
しかし,そのシステムには異なる複数の文字列が同じ文字列に暗号化されてしまうという問題点があった.
彼のシステムによって暗号化された文字列が与えられる.
元の文字列を復号するため,暗号化される前の文字列の候補をすべて列挙したい.
あなたの仕事はそのためのプログラムを作成することである.
小文字 a-z からなる文字列に対して,暗号化は次のステップに従って実行される.
- 最初に現れた ‘b’ を ‘a’ に置き換える.’b’ が存在しなければ何もしない.
- 最初に現れた ‘c’ を ‘b’ に置き換える.’c’ が存在しなければ何もしない.
…
- 最初に現れた ‘z’ を ‘y’ に置き換える.’z’ が存在しなければ何もしない.
Input
入力は100個以下のデータセットからなる.
各データセットは1行であり,暗号化後の文字列を表す.
文字列は小文字a-zからなり,1文字以上,20文字以下である.
入力の終わりは,1つの # のみを含む行で示される.
Output
各データセットに対して
暗号化する前の文字列の候補の数 n を1行目に出力し,
その後,暗号化前の文字列の候補を1行に1つずつ出力せよ.
もし n が10以下であれば,候補を辞書順ですべて出力し,
そうでなければ辞書順における先頭と末尾の5個ずつを辞書順で出力すること.
ここで辞書順は次のように再帰的に定義される.
空文字列は辞書順で最初に現れる.
2つの空でない文字列 x = x1 … xk と y = y1 … yl について,
文字列 x が辞書順で文字列 y より前であるとは,以下を満たすことをいう.
- x1 が y1 よりアルファベット順 (‘a’から’z’) で前である.または
- x1 と y1 が同じ文字であり x2 … xk が y2 … yl よりも辞書順で前に現れる
ことをいう.
Sample Input
enw abc abcdefghijklmnopqrst z #
Output for the Sample Input
1 fox 5 acc acd bbd bcc bcd 17711 acceeggiikkmmooqqssu acceeggiikkmmooqqstt acceeggiikkmmooqqstu acceeggiikkmmooqrrtt acceeggiikkmmooqrrtu bcdefghijklmnopqrrtt bcdefghijklmnopqrrtu bcdefghijklmnopqrssu bcdefghijklmnopqrstt bcdefghijklmnopqrstu 0
(End of Problem D) A B C D E F G
Problem E
橋の撤去
ICPC諸島は,かつて観光地として親しまれていたが,
このたび,自然保護のため,全ての人工施設を撤廃して人の立ち入りを禁止することが決定された.
このプロジェクトでいちばん難しいのは島々を結ぶ橋をすべて撤去することである.
ICPC諸島には島の数 n に対して n-1 個の橋があり,どの島から島へも,
橋を何回か渡れば到達することができるようになっている.
橋の撤去工事の作業チームは,好きな島からスタートして,繰り返し以下のいずれかの行動をとることができる.
- 今いる島に繋がっている橋を一つ渡って隣の島に移動する.
- 今いる島に繋がっている橋を一つ撤去する.撤去作業後は同じ島に留まる.
ただし当然ながら,一度撤去してしまった橋は二度と,どちらの方向にも渡ることができない.
橋を渡る場合も,橋を撤去する場合も,橋の長さに比例する時間がかかる.
全ての橋を撤去するのに必要な最短の時間を求めて欲しい.
作業チームのスタートする島と作業を終える島が異なっていても構わない.
Input
入力は100個以下のデータセットからなる.
各データセットは以下の形式をしている.
n
p2 p3 … pn
d2 d3 … dn
n は島の数 (3 ≤ n ≤ 800) を表す.島には 1 から n までの識別番号が振られている.
2行目には n-1 個の島番号が並べられており (1 ≤ pi < i),
2 から n までの島 i について i と pi
が橋で直接繋がれていることを意味する.
3行目の n-1 個の正整数は対応する橋の長さを表す (1 ≤ di ≤ 100,000).
すなわち,i と pi を結ぶ橋の長さは di である.
この橋を渡るのには di 単位の時間がかかり,撤去にも同じだけの時間がかかる.
なお,この入力形式では,全ての島と島の間が到達可能であるという条件は常に満たされている.
入力の終わりは,一つのゼロのみを含む行で示される.
Output
各データセットについて,全部の橋を撤去するのに必要な最短の単位時間数を,1行に出力せよ.
各出力行はこの数値以外の文字を含んではならない.
Sample Input
4 1 2 3 10 20 30 10 1 2 2 1 5 5 1 8 8 10 1 1 20 1 1 30 1 1 3 1 1 1 1 0
Output for the Sample Input
80 136 2
(End of Problem E) A B C D E F G
Problem F
サイコロ職人
サイコロ職人の朝は早い.
サイコロ職人であるあなたは,顧客からの注文を受け,日々様々なサイコロを製作している.
今日,あなたは正六面体の形状をしたサイコロで,6つの面のどこにでもよいから
t1, t2, …, t6
という数が印されたものを作って欲しい,という注文を受けた.
注文のサイコロを作るために,あなたは平らな板の形状をした専用工具を使う.
あなたは最初,各面に 0 が書かれたサイコロを持っている.
工具の上でサイコロを東西南北のいずれかの方向に 90 度回転させると,
新しく下に来た面に書かれた数が 1 増加する.
あなたは適切にサイコロを回転させることで,注文通りのサイコロを作ろうとしている.
最終的に面に書かれた数字は, 一連のステップでサイコロをどの方向に回転させるのかによって決まる.
各ステップでどの方向にサイコロを回転させたのかを表す文字列を操作列と呼ぶことにする.
正確には,次のように定義する.
n 回サイコロを回転させる操作列は n 文字からなる.
i ステップ目でサイコロを東方向に回転させた場合,操作列の i 文字目は E であるとする.
同様に,
西方向に回転させた場合は W,
南方向に回転させた場合は S,
北方向に回転させた場合は N であるとする.
たとえば,NWS という操作列は,最初に北方向にサイコロを回転させ,次に西方向に回転させ,最後に南方向に回転させる,という3回転の操作を表す.
注文を表す 6 つの整数が与えられるので,注文どおりのサイコロを作る操作列を求めて欲しい.
複数の操作列がありうるので,辞書順で最も前である操作列を求めてほしい.
Input
入力は複数のデータセットからなる.
データセットの個数は 40 個を超えない.
各データセットは次の形式で表される.
t1 t2 t3 t4 t5 t6
p q
t1, t2, …, t6 は注文を表す整数である.
また,p と q は正の整数であり,出力する操作列の範囲を表す (詳しくは下記を参照せよ).
各データセットは
0 ≤ t1 ≤ t2 ≤ … ≤ t6 ≤ 5,000
および
1 ≤ p ≤ q ≤ t1+t2+…+t6
を満たす.
入力は 6 つのゼロからなる行で終わる.
Output
各データセットについて,注文されたサイコロを作る辞書順で最小の操作列の p 文字目から q 文字目までを出力せよ (p 文字目と q 文字目も含む).
作ることができない場合,impossible と出力せよ.
ここで辞書順は次のように再帰的に定義される.
空文字列は辞書順で最初に現れる.
2つの空でない文字列 x = x1 … xk と y = y1 … yl について,文字列 x が文字列 y より辞書順で前であるとは,
- x1 が y1 よりアルファベット順 (‘A’から’Z’) で前である,または
- x1 と y1 が同じ文字であり x2 … xk が y2 … yl よりも辞書順で前である
ことをいう.
Sample Input
1 1 1 1 1 1 1 6 1 1 1 1 1 1 4 5 0 0 0 0 0 2 1 2 0 0 2 2 2 4 5 9 1 2 3 4 5 6 15 16 0 1 2 3 5 9 13 16 2 13 22 27 31 91 100 170 0 0 0 0 0 0
Output for the Sample Input
EEENEE NE impossible NSSNW EN EWNS SNSNSNSNSNSNSNSNSNSNSNSSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNWEWE
(End of Problem F) A B C D E F G
Problem G
円を横切るな!
平面上に 1 つ以上の円が配置されている.
任意の 2 つの円は,中心位置と半径の両方もしくは一方が異なる.
円は,他の円と共通領域をもつことはあるが,
3 つ以上の円が共通領域もしくは共通点をもつことはない.
円が,他の円を含むことや,2 点で交差することはあるが,
2 つの円の円周が 1 点で接することはないと仮定してよい.
あなたの仕事は,指定された 2 点 P と Q
を結ぶようなパスで,どの円弧とも交差しないものが存在するか,答えることである.
円の配置に対して,点の組は 1 組以上与えられる.
Figure G-1 の例では,円弧と交差することなく P と Q1 を結ぶことはできるが,円弧と交差することなく P と Q2, Q3, Q4 を結ぶことはできない.
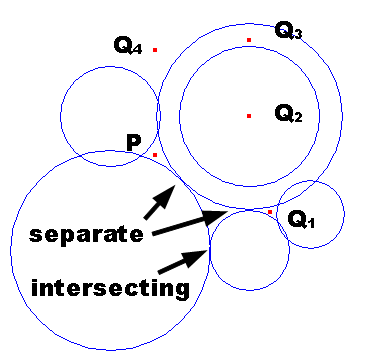
Input
入力は複数のデータセットからなり,
各データセットは次の形式で表される.
n m
Cx1 Cy1 r1
…
Cxn Cyn rn
Px1 Py1 Qx1 Qy1
…
Pxm Pym Qxm Qym
データセットの最初の行は,
空白文字 1 個で区切られた 2 個の整数 n, m からなる.
n は,円の個数であり,1 ≤ n ≤ 100 と仮定してよい.
m は,点の組の個数であり,1 ≤ m ≤ 10
と仮定してよい.
続く n 行のそれぞれは,空白文字 1 個で区切られた 3 個の整数からなる.
(Cxi, Cyi) と ri は,
i 番目の円の中心の位置と半径を表す.
引き続く m 行のそれぞれは,空白文字 1 個で区切られた 4 個の整数からなる.
この 4 個の整数は 2 つの異なる点
Pj = (Pxj, Pyj) と
Qj =(Qxj, Qyj)
の座標を与える.
この 2 点 Pj と Qj
が j 番目の点の組である.
0 ≤ Cxi ≤ 10000,
0 ≤ Cyi ≤ 10000,
1 ≤ ri ≤ 1000,
0 ≤ Pxj ≤ 10000,
0 ≤ Pyj ≤ 10000,
0 ≤ Qxj ≤ 10000,
0 ≤ Qyj ≤ 10000 と仮定してよい.
また,Pj および Qj は,どの円の円周上にも存在することはない.
入力の終わりは,空白文字 1 個で区切られた 2 個のゼロからなる行で表される.
なお,図 G-1 は,後に示す Sample Input 中の最初のデータセットにおける
円と点の配置を表している.
図 G-2 は,Sample Input 中の残りのデータセットにおける配置を表している.
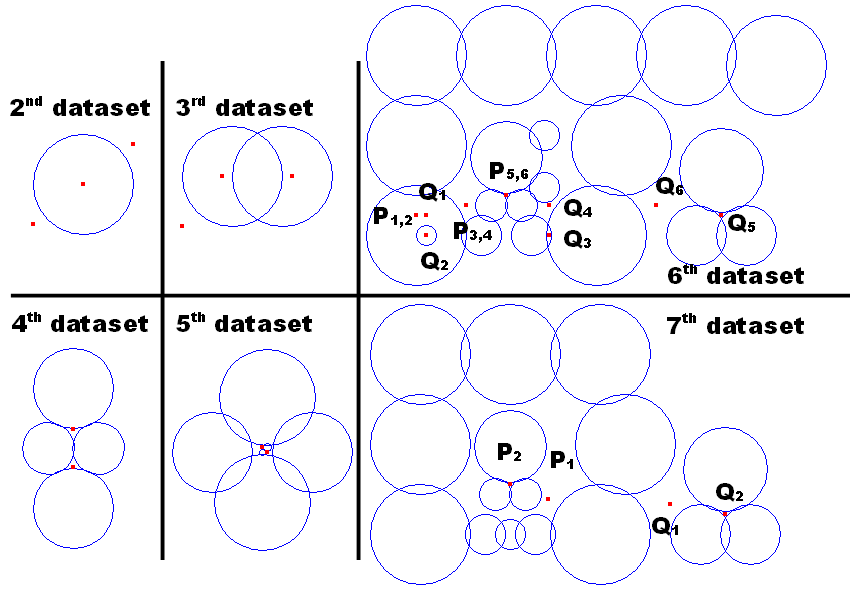
Output
各データセットに対して,
m 個の結果を,空白文字 1 個で区切って,1 行に出力せよ.
ただし,j 番目の結果には Pj と Qj を
結ぶパスが存在する場合は “YES” を,存在しない場合は
“NO” を出力すること.
Sample Input
5 3 0 0 1000 1399 1331 931 0 1331 500 1398 0 400 2000 360 340 450 950 1600 380 450 950 1399 1331 450 950 450 2000 1 2 50 50 50 0 10 100 90 0 10 50 50 2 2 50 50 50 100 50 50 40 50 110 50 40 50 0 0 4 1 25 100 26 75 100 26 50 40 40 50 160 40 50 81 50 119 6 1 100 50 40 0 50 40 50 0 48 50 50 3 55 55 4 55 105 48 50 55 55 50 20 6 270 180 50 360 170 50 0 0 50 10 0 10 0 90 50 0 180 50 90 180 50 180 180 50 205 90 50 180 0 50 65 0 20 75 30 16 90 78 36 105 30 16 115 0 20 128 48 15 128 100 15 280 0 30 330 0 30 305 65 42 0 20 10 20 0 20 10 0 50 30 133 0 50 30 133 30 90 40 305 20 90 40 240 30 16 2 0 0 50 0 90 50 0 180 50 90 180 50 180 180 50 205 90 50 180 0 50 65 0 20 115 0 20 90 0 15 280 0 30 330 0 30 305 65 42 75 40 16 90 88 36 105 40 16 128 35 250 30 90 50 305 20 0 0
Output for the Sample Input
YES NO NO YES NO NO NO NO YES YES NO NO YES NO NO NO NO