Mammy decided to give Taro his first shopping experience. Mammy tells him to choose any two items he wants from those listed in the shopping catalogue, but Taro cannot decide which two, as all the items look attractive. Thus he plans to buy the pair of two items with the highest price sum, not exceeding the amount Mammy allows. As getting two of the same item is boring, he wants two different items.

You are asked to help Taro select the two items. The price list for all of the items is given. Among pairs of two items in the list, find the pair with the highest price sum not exceeding the allowed amount, and report the sum. Taro is buying two items, not one, nor three, nor more. Note that, two or more items in the list may be priced equally.

The input consists of multiple datasets, each in the following format.

n m
a₁ a₂ … a_n

A dataset consists of two lines. In the first line, the number of items n and the maximum payment allowed m are given. n is an integer satisfying 2 ≤ n ≤ 1000. m is an integer satisfying 2 ≤ m ≤ 2,000,000. In the second line, prices of n items are given. a_i (1 ≤ i ≤ n) is the price of the i-th item. This value is an integer greater than or equal to 1 and less than or equal to 1,000,000.

The end of the input is indicated by a line containing two zeros. The sum of n's of all the datasets does not exceed 50,000.

For each dataset, find the pair with the highest price sum not exceeding the allowed amount m and output the sum in a line. If the price sum of every pair of items exceeds m, output NONE instead.

3 45
10 20 30
6 10
1 2 5 8 9 11
7 100
11 34 83 47 59 29 70
4 100
80 70 60 50
4 20
10 5 10 16
0 0

40
10
99
NONE
20

The programming contest named Concours de Programmation Comtemporaine Interuniversitaire (CPCI) has a judging system similar to that of ICPC; contestants have to submit correct outputs for two different inputs to be accepted as a correct solution. Each of the submissions should include the program that generated the output. A pair of submissions is judged to be a correct solution when, in addition to the correctness of the outputs, they include an identical program.

Many contestants, however, do not stop including a different version of their programs in their second submissions, after modifying a single string literal in their programs representing the input file name, attempting to process different input. The organizers of CPCI are exploring the possibility of showing a special error message for such close submissions, indicating contestants what's wrong with such submissions. Your task is to detect such close submissions.

The input consists of at most 100 datasets, each in the following format.

s₁
s₂

Each of s₁ and s₂ is a string written in a line, with the length between 1 and 200, inclusive. They are the first and the second submitted programs respectively. A program consists of lowercase letters (a, b, ..., z), uppercase letters (A, B, ..., Z), digits (0, 1, ..., 9), double quotes ("), and semicolons (;). When double quotes occur in a program, there are always even number of them.

The end of the input is indicated by a line containing one ‘.’ (period).

For each dataset, print the judge result in a line.

If the given two programs are identical, print IDENTICAL. If two programs differ with only one corresponding string literal, print CLOSE. Otherwise, print DIFFERENT. A string literal is a possibly empty sequence of characters between an odd-numbered occurrence of a double quote and the next occurrence of a double quote.

print"hello";print123
print"hello";print123
read"B1input";solve;output;
read"B2";solve;output;
read"C1";solve;output"C1ans";
read"C2";solve;output"C2ans";
""""""""
"""42"""""
slow"program"
fast"code"
"super"fast"program"
"super"faster"program"
X""
X
I"S""CREAM"
I"CE""CREAM"
11"22"11
1"33"111
.

IDENTICAL
CLOSE
DIFFERENT
CLOSE
DIFFERENT
DIFFERENT
DIFFERENT
CLOSE
DIFFERENT

Mr. Gardiner is a modern garden designer who is excellent at utilizing the terrain features. His design method is unique: he first decides the location of ponds and design them with the terrain features intact.

According to his unique design procedure, all of his ponds are rectangular with simple aspect ratios. First, Mr. Gardiner draws a regular grid on the map of the garden site so that the land is divided into cells of unit square, and annotates every cell with its elevation. In his design method, a pond occupies a rectangular area consisting of a number of cells. Each of its outermost cells has to be higher than all of its inner cells. For instance, in the following grid map, in which numbers are elevations of cells, a pond can occupy the shaded area, where the outermost cells are shaded darker and the inner cells are shaded lighter. You can easily see that the elevations of the outermost cells are at least three and those of the inner ones are at most two.

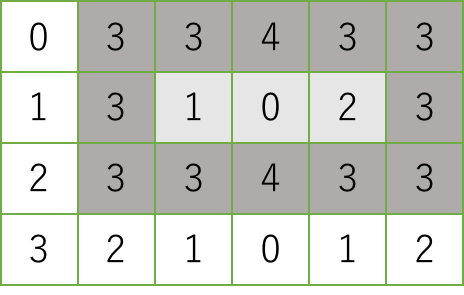
A rectangular area on which a pond is built must have at least one inner cell. Therefore, both its width and depth are at least three.

When you pour water at an inner cell of a pond, the water can be kept in the pond until its level reaches that of the lowest outermost cells. If you continue pouring, the water inevitably spills over. Mr. Gardiner considers the larger capacity the pond has, the better it is. Here, the capacity of a pond is the maximum amount of water it can keep. For instance, when a pond is built on the shaded area in the above map, its capacity is (3 − 1) + (3 − 0) + (3 − 2) = 6, where 3 is the lowest elevation of the outermost cells and 1, 0, 2 are the elevations of the inner cells. Your mission is to write a computer program that, given a grid map describing the elevation of each unit square cell, calculates the largest possible capacity of a pond built in the site.

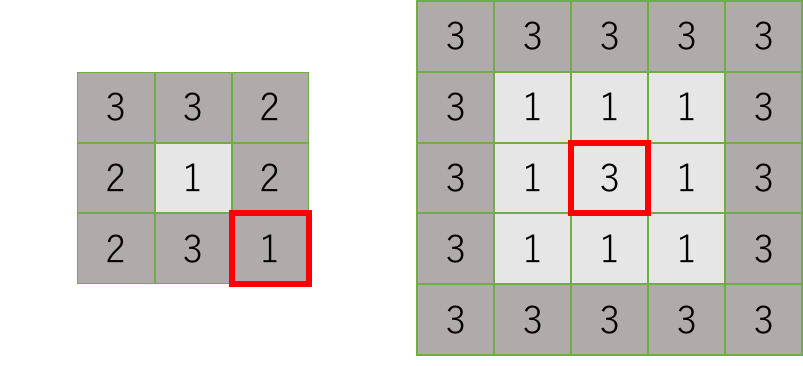
Note that neither of the following rectangular areas can be a pond. In the left one, the cell at the bottom right corner is not higher than the inner cell. In the right one, the central cell is as high as the outermost cells.

The input consists of at most 100 datasets, each in the following format.

d w
e_{1, 1} ... e_{1, w}
...
e_{d, 1} ... e_{d, w}

The first line contains d and w, representing the depth and the width, respectively, of the garden site described in the map. They are positive integers between 3 and 10, inclusive. Each of the following d lines contains w integers between 0 and 9, inclusive, separated by a space. The x-th integer in the y-th line of the d lines is the elevation of the unit square cell with coordinates (x, y).

The end of the input is indicated by a line containing two zeros separated by a space.

For each dataset, output a single line containing the largest possible capacity of a pond that can be built in the garden site described in the dataset. If no ponds can be built, output a single line containing a zero.

3 3
2 3 2
2 1 2
2 3 1
3 5
3 3 4 3 3
3 1 0 2 3
3 3 4 3 2
7 7
1 1 1 1 1 0 0
1 0 0 0 1 0 0
1 0 1 1 1 1 1
1 0 1 0 1 0 1
1 1 1 1 1 0 1
0 0 1 0 0 0 1
0 0 1 1 1 1 1
6 6
1 1 1 1 2 2
1 0 0 2 0 2
1 0 0 2 0 2
3 3 3 9 9 9
3 0 0 9 0 9
3 3 3 9 9 9
0 0

0
3
1
9

Taro has been hooked on making lunch boxes recently. Taro has obtained a new lunch box recipe book today, and wants to try as many of the recipes listed in the book as possible.

Enough of the ingredients for all the recipes are at hand, but they all are in vacuum packs of two. If only one of them is used leaving the other, the leftover will be rotten easily, but making two of the same recipe is not interesting. Thus he decided to make a set of lunch boxes, each with different recipe, that wouldn't leave any unused ingredients.

Note that the book may include recipes for different lunch boxes made of the same set of ingredients.

How many lunch box recipes can Taro try today at most following his dogma?

The input consists of at most 50 datasets, each in the following format.

n m
b_1,1...b_1,m
...
b_n,1...b_n,m

The first line contains n, which is the number of recipes listed in the book, and m, which is the number of ingredients. Both n and m are positive integers and satisfy 1 ≤ n ≤ 500, 1 ≤ m ≤ 500 and 1 ≤ n × m ≤ 500. The following n lines contain the information for each recipe with the string of length m consisting of 0 or 1. b_i,j implies whether the i-th recipe needs the j-th ingredient. 1 means the ingredient is needed for the recipe and 0 means not. Each line contains at least one 1.

The end of the input is indicated by a line containing two zeros.

For each dataset, output the maximum number of recipes Taro can try.

4 3
110
101
011
110
7 1
1
1
1
1
1
1
1
4 5
10000
01000
00100
00010
6 6
111111
011000
100000
000010
100001
100100
0 0

3
6
0
6

You are asked to build a compressor for Boolean expressions that transforms expressions to the shortest form keeping their meaning.

The grammar of the Boolean expressions has terminals 0 1 a b c d - ^ * ( ), start symbol <E> and the following production rule:

<E>  ::=  0  |  1  |  a  |  b  |  c  |  d  |  -<E>  |  (<E>^<E>)  |  (<E>*<E>)

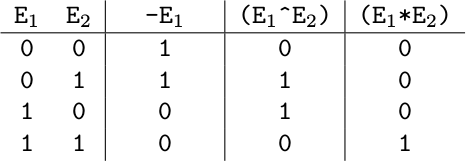
Letters a, b, c and d represent Boolean variables that have values of either 0 or 1. Operators are evaluated as shown in the Table below. In other words, - means negation (NOT), ^ means exclusive disjunction (XOR), and * means logical conjunction (AND).

Table: Evaluations of operators

Write a program that calculates the length of the shortest expression that evaluates equal to the given expression with whatever values of the four variables.

For example, 0, that is the first expression in the sample input, cannot be shortened further. Therefore the shortest length for this expression is 1.

For another example, (a*(1*b)), the second in the sample input, always evaluates equal to (a*b) and (b*a), which are the shortest. The output for this expression, thus, should be 5.

The input consists of multiple datasets. A dataset consists of one line, containing an expression conforming to the grammar described above. The length of the expression is less than or equal to 16 characters.

The end of the input is indicated by a line containing one ‘.’ (period). The number of datasets in the input is at most 200.

For each dataset, output a single line containing an integer which is the length of the shortest expression that has the same value as the given expression for all combinations of values in the variables.

0
(a*(1*b))
(1^a)
(-(-a*-b)*a)
(a^(b^(c^d)))
.

1
5
2
1
13

Think of repetitively folding a very long and thin ribbon. First, the ribbon is spread out from left to right, then it is creased at its center, and one half of the ribbon is laid over the other. You can either fold it from the left to the right, picking up the left end of the ribbon and laying it over the right end, or from the right to the left, doing the same in the reverse direction. To fold the already folded ribbon, the whole layers of the ribbon are treated as one thicker ribbon, again from the left to the right or the reverse.

After folding the ribbon a number of times, one of the layers of the ribbon is marked, and then the ribbon is completely unfolded restoring the original state. Many creases remain on the unfolded ribbon, and one certain part of the ribbon between two creases or a ribbon end should be found marked. Knowing which layer is marked and the position of the marked part when the ribbon is spread out, can you tell all the directions of the repeated folding, from the left or from the right?

The figure below depicts the case of the first dataset of the sample input.

Input

The input consists of at most 100 datasets, each being a line containing three integers.

n i j

The three integers mean the following: The ribbon is folded n times in a certain order; then, the i-th layer of the folded ribbon, counted from the top, is marked; when the ribbon is unfolded completely restoring the original state, the marked part is the j-th part of the ribbon separated by creases, counted from the left. Both i and j are one-based, that is, the topmost layer is the layer 1 and the leftmost part is numbered 1. These integers satisfy 1 ≤ n ≤ 60, 1 ≤ i ≤ 2ⁿ, and 1 ≤ j ≤ 2ⁿ.

The end of the input is indicated by a line with three zeros.

Output

For each dataset, output one of the possible folding sequences that bring about the result specified in the dataset.

The folding sequence should be given in one line consisting of n characters, each being either L or R. L means a folding from the left to the right, and R means from the right to the left. The folding operations are to be carried out in the order specified in the sequence.

Sample Input

3 3 2
12 578 2214
59 471605241352156968 431565444592236940
0 0 0

Output for the Sample Input

LRR
RLLLRRRLRRLL
LRRRLRRLLRRRRLLLLRLLRRRLRRLLRLLLLLLRLRLLRLRLLLRLRLLRLLRRRLL

Explorer Taro got a floor plan of a labyrinth. The floor of this labyrinth is in the form of a two-dimensional grid. Each of the cells on the floor plan corresponds to a room and is indicated whether it can be entered or not. The labyrinth has only one entrance located at the northwest corner, which is upper left on the floor plan. There is a treasure chest in each of the rooms at other three corners, southwest, southeast, and northeast. To get a treasure chest, Taro must move onto the room where the treasure chest is placed.

Taro starts from the entrance room and repeats moving to one of the enterable adjacent rooms in the four directions, north, south, east, or west. He wants to collect all the three treasure chests and come back to the entrance room. A bad news for Taro is that, the labyrinth is quite dilapidated and even for its enterable rooms except for the entrance room, floors are so fragile that, once passed over, it will collapse and the room becomes not enterable. Determine whether it is possible to collect all the treasure chests and return to the entrance.

The input consists of at most 100 datasets, each in the following format.

N M
c_1,1...c_1,M
...
c_N,1...c_N,M

The first line contains N, which is the number of rooms in the north-south direction, and M, which is the number of rooms in the east-west direction. N and M are integers satisfying 2 ≤ N ≤ 50 and 2 ≤ M ≤ 50. Each of the following N lines contains a string of length M. The j-th character c_i,j of the i-th string represents the state of the room (i,j), i-th from the northernmost and j-th from the westernmost; the character is the period ('.') if the room is enterable and the number sign ('#') if the room is not enterable. The entrance is located at (1,1), and the treasure chests are placed at (N,1), (N,M) and (1,M). All of these four rooms are enterable. Taro cannot go outside the given N × M rooms.

The end of the input is indicated by a line containing two zeros.

For each dataset, output YES if it is possible to collect all the treasure chests and return to the entrance room, and otherwise, output NO in a single line.

3 3
...
.#.
...
5 5
..#..
.....
#....
.....
.....
3 8
..#.....
........
.....#..
3 5
..#..
.....
..#..
4 4
....
....
..##
..#.
0 0

YES
NO
YES
NO
NO

Two triangles T₁ and T₂ with the same area are on a plane. Your task is to perform the following operation to T₁ several times so that it is exactly superposed on T₂. Here, vertices of T₁ can be on any of the vertices of T₂. Compute the minimum number of operations required to superpose T₁ on T₂.

(Operation): Choose one vertex of the triangle and move it to an arbitrary point on a line passing through the vertex and parallel to the opposite side.

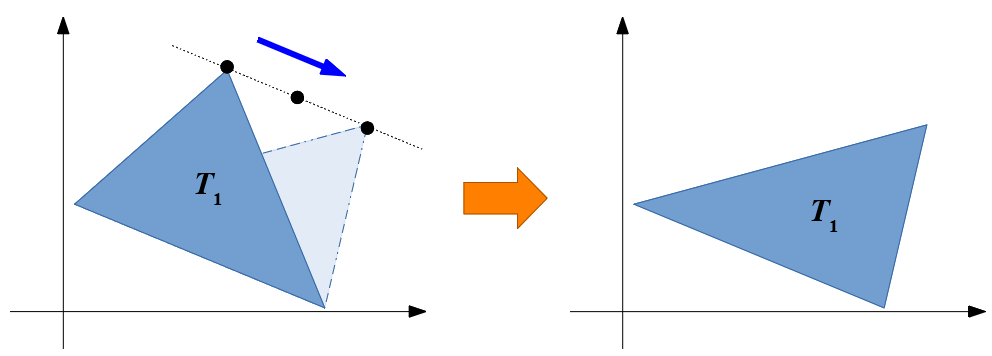
An operation example

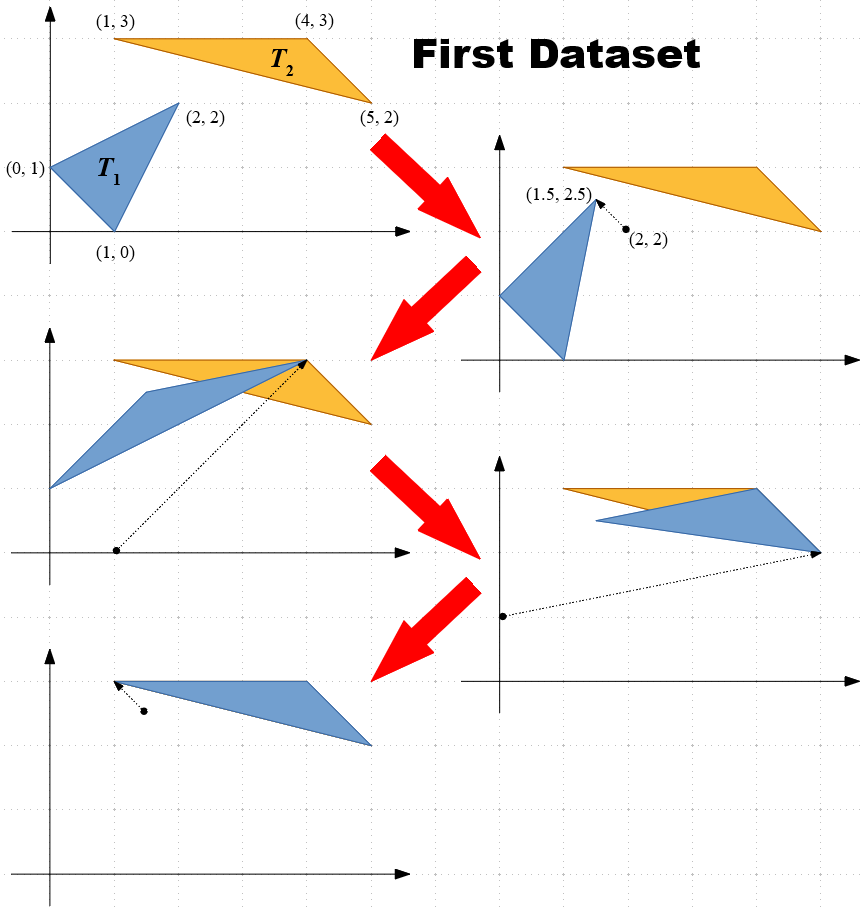
The following figure shows a possible sequence of the operations for the first dataset of the sample input.

The input consists of at most 2000 datasets, each in the following format.

x₁₁ y₁₁
x₁₂ y₁₂
x₁₃ y₁₃
x₂₁ y₂₁
x₂₂ y₂₂
x₂₃ y₂₃

x_ij and y_ij are the x- and y-coordinate of the j-th vertex of T_i.

The following holds for the dataset.

• All the coordinate values are integers with at most 1000 of absolute values.
• T₁ and T₂ have the same positive area size.
• The given six vertices are all distinct points.

An empty line is placed between datasets.

The end of the input is indicated by EOF.

For each dataset, output the minimum number of operations required in one line. If five or more operations are required, output Many instead.

Note that, vertices may have non-integral values after they are moved.

You can prove that, for any input satisfying the above constraints, the number of operations required is bounded by some constant.

0 1
2 2
1 0
1 3
5 2
4 3

0 0
0 1
1 0
0 3
0 2
1 -1

-5 -4
0 1
0 15
-10 14
-5 10
0 -8

-110 221
-731 525
-555 -258
511 -83
-1000 -737
66 -562

533 -45
-525 -450
-282 -667
-439 823
-196 606
-768 -233

0 0
0 1
1 0
99 1
100 1
55 2

354 -289
89 -79
256 -166
131 -196
-774 -809
-519 -623

-990 688
-38 601
-360 712
384 759
-241 140
-59 196

629 -591
360 -847
936 -265
109 -990
-456 -913
-787 -884

-1000 -1000
-999 -999
-1000 -998
1000 1000
999 999
1000 998

-386 -83
404 -83
-408 -117
-162 -348
128 -88
296 -30

-521 -245
-613 -250
797 451
-642 239
646 309
-907 180

-909 -544
-394 10
-296 260
-833 268
-875 882
-907 -423

4
3
3
3
3
4
4
4
4
Many
Many
Many
Many