東京 2020 オリンピック・パラリンピックのカウントダウンは 2021 年夏まで続く．それはさておき，あなたには整数の並びの中に 2, 0, 2, 0 のよっつの整数がこの順に続けて現れる回数をカウントアップして欲しい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
d₁ … d_n

各データセットは 2 行からなる． 最初の行には 2 行目に並ぶ整数の個数 n (4 ≤ n ≤ 1000) がある． 次の行には空白で区切られた n 個の整数 d₁, …, d_n がある． ここで d₁ から d_n はすべて 0 以上 9 以下である．

入力の終わりはゼロひとつを含む行で示す．

データセットは 100 個以内である．

各データセットに対して，2 行目の整数の並びの中によっつの整数 2, 0, 2, 0 がこの順に続けて現れる回数を 1 行に出力せよ． 重なり合う出現は個別に数える． たとえば “2 0 2 0 2 0 2 0” には 2 回ではなく 3 回現れるものとする．

15
2 0 2 0 2 2 0 2 0 2 2 0 2 0 2
20
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
32
1 8 1 9 1 9 2 0 2 0 2 1 2 1 2 2 2 2 2 1 2 1 2 0 2 0 1 9 1 9 1 8
32
2 0 1 8 2 0 1 9 2 0 2 0 2 0 2 1 2 0 2 2 2 0 2 3 2 0 2 1 2 0 2 0
0
  

3
0
2
3

新種のウイルスの感染が拡大している． このウイルスはキャリアとの濃厚接触による感染リスクがあり， それはキャリアの症状の有無によらないことが知られている． このため，感染が確認された者やその疑いの強い者と濃厚接触があった者を特定して検査することが防疫上有効である． そこで，普段から人と人との接触を携帯電話上のアプリをもちいてすべて記録しておき， 感染確認時にはその記録に基づいて直接・間接の感染リスクがある人を特定するシステムを構築したい．

あなたは，こうしたシステムの開発を任された．そして，既に携帯電話側のアプリは完成させた． インストールしたアプリが， 同じアプリをインストールした携帯電話を持っている人との濃厚接触を検知すると， 両者の ID を情報収集センターに送信する．

あなたの次の仕事は，利用者の感染が確認されたときに， その感染者から直接的または間接的に感染したリスクがある利用者を特定するプログラムを作ることである．

システムの利用者の感染が確認されたら， それ以前のある期間 (感染性保持期間) 内に濃厚接触した利用者は感染の疑いがある． 感染が疑われる利用者がその後にまた別の利用者と濃厚接触していれば， その相手にもまた感染の疑いがある． こうして感染の疑いは繰り返し広がるものとする．

ある利用者の感染が確認されると，その利用者の ID と， その利用者がキャリアになった可能性がある時刻以降の， すべての利用者同士の濃厚接触の記録が入力として与えられる． 与えられた記録にある濃厚接触はすべて， 感染が確認された利用者の感染性保持期間内に起こったと仮定する． 出力は感染が確認された利用者から直接的または間接的に感染した疑いがある利用者の総数である．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

m n p
a₁ b₁
…
a_n b_n

各データセットは三つの整数 m，n，p からなる行から始まる． m (1 ≤ m ≤ 100) は利用者の人数を表す． n (0 ≤ n ≤ 1000) は記録の件数を表す． p (1 ≤ p ≤ m) は感染が確認された利用者の ID を表す．

続く n 行には利用者同士の濃厚接触の記録が 1 行に 1 件ずつ時刻順に並んでいる． 各行は，ID が a_i と b_i の利用者の濃厚接触があったことを表す． ここで， 1 ≤ a_i ≤ m, 1 ≤ b_i ≤ m かつ a_i ≠ b_i である．

入力の終わりは三つのゼロからなる行で表される．データセットの個数は 50 を超えない．

各データセットについて， 感染が確認された利用者とその利用者から直接的または間接的に感染した疑いがある利用者の総数を出力せよ．

3 2 1
1 2
2 3
4 5 2
1 3
3 4
2 1
3 1
1 2
100 0 100
0 0 0

3
3
1

横浜君はいくつかの荷物の配送料金を見積もるところだ． 荷物の配送料金は，それぞれ整数値に切り上げられた， 幅 w, 奥行 d, 高さ h に基づいている． 配送料金はそれらの「和」に比例する．

配送する荷物の一覧はあるのだが，手違いにより そこにあるのは各荷物の幅，奥行，高さの「積」 w×d×h であって， 「和」 w+d+h ではない． この情報だけでは配送料金を正確に計算できない．

そこで横浜君は配送料金の最小値を見積もることにした． そのためには一覧中に記された各荷物の「積」 p に対して， p=w×d×h を満たす 最小の「和」 s=w+d+h を求める必要がある．

あなたには， 与えられた積 p に対して， 和の最小値 s を計算するプログラムを書いて横浜君を助けてほしい．

入力は複数のデータセットからなる． 各データセットは 1 行で，ひとつの整数 p (0 < p < 10¹⁵) が記されている．

入力の終わりは，ゼロひとつからなる行で表される．

データセットは300個以内である．

各データセットについて，整数 s ひとつからなる行を出力せよ． s は p=w×d×h を満たすみっつの正整数 w, d, h の和 w+d+h の最小値である.

1
2
6
8
729
47045881
12137858827249
562949953421312
986387345919360
999730024299271
999998765536093
0

3
4
6
6
27
1083
6967887
262144
298633
299973
999998765536095

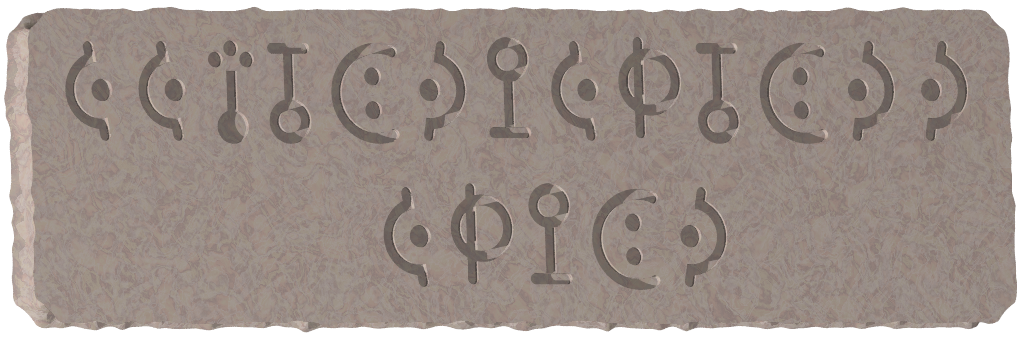
先史文明研究センター (Investigation Center for Prehistoric Civilization, ICPC) は Icpca 古王国文明を調査してきた． 先日の Icpca の廃墟の発掘では石壁に刻まれたふたつの式を発見した． 式は n 種類の Icpca 文字 a₁, ..., a_n と不等号 ('<' と '>') および括弧 ('(' と ')') に相当する記号からなるが，記述の都合上，以下ではこれらを英大文字や通常の記号で表すことにする． 式は以下の文法規則 (開始記号 E) に従っている．

  E ::= F | '(' E '<' E ')' | '(' E '>' E ')'
  F ::= a1 | a2 | … | an

古王国とその文明についての多様な知見を総合した分析から，以下の評価規則が判明した．

• 文字 a₁, ..., a_n の集合にはある全順序が定められている．
• 式が文字ひとつからなるとき，その値はその文字そのものである．
• ふたつの式 P と Q の値がそれぞれ a_i と a_j であるとき，式 (P<Q) の値は，a_i と a_j のうち全順序で先に来る方の文字である．両者が同じ文字なら値はその文字である．
• 同様に，ふたつの式 P と Q の値がそれぞれ a_i と a_j であるとき，式 (P>Q) の値は，a_i と a_j のうち全順序で後に来る方の文字である．両者が同じ文字なら値はその文字である．

発見されたふたつの式の値は等しいはずであることもわかった． 考えられる n! 種の全順序のうち，両式の値が等しくなるような全順序は何種類存在するだろうか．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
a₁a₂...a_n
S
T

各データセットは 4 行からなる． 1 行目には，Icpca 文字に対応する英大文字の種類数 n (1 ≤ n ≤ 16) が与えられる． 2 行目には，n 種の相異なる英大文字が区切りなしで与えられる． 3 行目と 4 行目には，それぞれ発見されたふたつの式 S と T が与えられる． S と T は共に 100 文字以内であり，上述の文法に従う．

入力の終わりは，ゼロひとつからなる行で表される． データセットの個数は 50 を超えない．

各データセットについて，発見されたふたつの式の値が等しくなるような全順序の種類数を 1 行に出力せよ．

3
CIP
((I<C)>(P<C))
(P>C)
2
AB
(A<B)
(A>B)
3
ANY
((A<N)<Y)
((N<Y)<((A<A)<N))
6
ANSWER
A
((E>(A>((E<W)>(N<S))))>(A<W))
0

1
0
6
300

N 行 M 列の格子状に点が並んでいる． 各点を，その行番号 i (1 ≤ i ≤ N) と列番号 j (1 ≤ j ≤ M) を用いて P_{i, j} と呼ぶことにする．

各点は白か黒に塗られている．白い点からなる集合 T のうち，以下の制約を満たすものの個数を計算せよ．

• ∀i ∈ {3, 4,..., N}, ∀j ∈ {2, 3,..., M}, P_{i, j} ∈ T ⇒ P_{i -2, j -1} ∉ T,
• ∀i ∈ {3, 4,..., N}, ∀j ∈ {1, 2,..., M−1}, P_{i, j} ∈ T ⇒ P_{i -2, j +1} ∉ T.

例えば下図で☆の位置にある点を選ぶと，×の付けられた2つの点はどちらも選ぶことができない．

将棋を知っている人は， ☆と×をつけた点の相対位置と桂馬の動きの共通性に気づくだろう．

答えは巨大になる可能性があるため， 10⁹+7 で割った余りを出力せよ．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

N M
a_1,1 ... a_1,M
...
a_N,1 ... a_N,M

各データセットの一行目には二つの整数 N (2 ≤ N ≤ 60) と M (2 ≤ M ≤ 60) が与えられ，それぞれ行数と列数を表す． 続く N 行にはそれぞれ M 文字が与えられる． i 番目の文字列の j 文字目 a_i,j は点 P_{i, j} の色を表し，'.' は白色，'#' は黒色であることを示す．

入力の終わりは，二つのゼロのみからなる行で表される．

データセットは 100 個以内である．

各データセットについて，条件を満たす部分集合の個数を 10⁹+7 で割った余りを一行に出力せよ．

3 2
.#
##
#.
3 3
.#.
#.#
..#
6 5
.#..#
...#.
#....
..#.#
#....
..#..
0 0

3
20
103320

あなたの住む市の市議会は，災害時のための避難所を一つ建設することを決定した． 避難所は，災害によって道路が寸断されるような状況であっても， 市内のできるだけ多くの地点から到達可能であることが望ましい． 市の道路網が与えられるので，最適な建設候補地を見つけて欲しい．

道路網は，無向グラフとして与えられる．市内の地点がグラフの頂点であり， 辺は地点同士を結ぶ双方向の道である． また，それぞれの道には，災害に対する推定強度を示す正の整数が与えられている． 推定強度 s の道は，災害レベル s 未満の災害時には通行可能だが， s 以上の災害が発生すると通れなくなると推定されている．

避難所としての適切さの度合いは，以下の順序関係によって評価するものとする． 災害レベル s の災害発生時に通行可能な道で地点 v まで到達できる地点の数を r_s(v) とする． 地点 u と地点 v について，ある k ≥ 1 があって，

• r₁(u) = r₁(v),
• r₂(u) = r₂(v),
• ...
• r_k-1(u) = r_k-1(v),
• r_k(u) > r_k(v)

が成り立つとき，かつそのときに限り，地点 u の方が v よりも避難所に適しているとする． この基準に基づいて，避難所として最適な地点 (同評価の地点が複数あればその全て) を求めて欲しい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m
a₁ b₁ s₁
...
a_m b_m s_m

n は 10⁵ 以下の正の整数であり，地点の数を表す． m は 10⁵ 以下の非負整数であり，道の数を表す． 各地点には 1 から n までの識別番号が振られている． i 番目の道は地点 a_i と b_i を結んでおり， その推定強度は s_i である． a_i, b_i, s_i はそれぞれ整数であり， 1 ≤ a_i < b_i ≤ n および 1 ≤ s_i ≤ 10⁵ を満たす． i ≠ j のとき，a_i ≠ a_j または b_i ≠ b_j である． 与えられるグラフは連結である． すなわち，任意の二つの地点を結ぶ経路が存在する．

入力の終わりは二つのゼロからなる行で表される． データセットの個数は 50 を超えない．

各データセットについて上述の基準に照らして最適である地点 (同評価の地点が複数あればその全て) の地点識別番号のリストを，1 行に空白区切りで小さい順に出力せよ．

3 3
1 2 1
1 3 2
2 3 3
3 3
1 2 3
1 3 3
2 3 3
5 5
1 2 5
2 3 1
3 4 2
3 5 1
4 5 2
0 0

2 3
1 2 3
3 4 5

ICPC 社の社員であるあなたは，新しいオフィスでの座席の配置の計画を任された． あなたの仕事は，三密回避のための条件を守りつつ室内になるべく多くの座席を配置することである． そこで，あなたはグリッドを用いたシミュレーションで問題を解くことにした．

シミュレーションでは部屋を長方形のグリッドで表す． グリッドの各マスは座席を配置できる空マスか，配置できない壁マスのいずれかである． 座席間の間隔を確保するため，各空マスに配置できる座席は高々ひとつである．

ここで，グリッドの北西角のマスから始めて，東または南に隣接する空マスに移ることを繰り返し， 南東角のマスに至る経路を「換気経路」と呼ぶことにする． 換気経路は一般には多数存在する． 座席を配置するどのマスについても，そこを通る換気経路が少なくともひとつは存在していなくてはならない． また，換気経路中の座席を配置するマスの数を「座席経由数」と呼ぶとき， どの換気経路の座席経由数もあらかじめ定められた許容最大値以下でなければならない． 上記の条件を満たしてなるべく多くの座席を配置する方法を考えて欲しい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m k
a_1,1…a_1,m
…
a_n,1…a_n,m

n, m はそれぞれグリッドの縦横のマスの数を表す． n, m は，正の整数であり，20 を超えない． k は座席経由数の許容最大値を表す． k は，正の整数であり，n + m − 1 を超えない． 続く n 行はそれぞれm 文字からなり， 各文字は '.' または '#' のいずれかである． グリッドの i 行 j 列目のマスは a_i,j が '.' なら空マス， '#' なら壁マスである． 第 1 行第 1 列が部屋の北西角，第 n 行第 m 列が南東角に対応する．

入力の終わりは三つのゼロからなる行で表される． データセットの個数は 100 を超えない．

各データセットについて，以下の n + 1 行を出力せよ． まず，1 行目に配置できる座席の最大数を 1 行に出力せよ． 2 行目以降には具体的な座席数が最大となる配置のひとつを出力せよ． 配置の出力は入力と同様の形式とし， 座席を配置する空マスを '.' から '@' に変更したもので表せ． 最大数の座席を収容できる配置が複数存在する場合は， 各行の文字列を連結したときに ASCII 順序で辞書順最小になるものを求めよ． ASCII コードは '#' < '.' < '@' の順である．

3 3 3
...
.#.
...
3 3 1
...
.#.
...
6 11 1
...........
.....#.....
.....#.....
.....#.....
.....#.....
...........
7 7 3
.......
.##.##.
.#...#.
.#...#.
.#...#.
.##.##.
.......
0 0 0

6
.@@
@#@
@@.
2
...
.#@
.@.
10
..........@
....@#...@.
...@.#..@..
..@..#.@...
.@...#@....
@..........
9
.......
.##.##.
.#...#.
.#.@.#@
.#.@.#@
.##@##@
@@@....

理想キャニスタ (英語名 Ideally Compact Packaging Canisters, ICPC) 株式会社は， キャニスタ (円筒型容器) の専門メーカーで， 顧客の注文に応じたキャニスタを設計・製造している．

同社は異なる製品二つを一緒に入れるキャニスタの注文を受けた． 製品の形状は共に凸多角柱で，高さはまったく同じである． キャニスタの内側は，高さが製品の高さと等しい精密な円柱状にしたい．

製品はキャニスタ内に縦向きに配置されなければならない． すなわち，どちらの製品の底面も容器の底面に沿って配置しなければならない． 製品はキャニスタ内のどこにどの向きに置いても良いが， 上下逆さまに置いてはならないし， 製品を重ねて置いてもならない． 製品同士や容器の内面が接触するのは構わない．

注文主はキャニスタをなるべく小さくしたいと望んている． あなたには二つの製品が収まるキャニスタの底面の最小直径を見つけてほしい．

入力は高々 50 個のデータセットからなる． 各データセットは次の形式で表される．

n
x_a,1 y_a,1
...
x_a,n y_a,n
m
x_b,1 y_b,1
...
x_b,m y_b,m

n (3 ≤ n ≤ 40) は片方の製品の底面の多角形の頂点数である． 続く n 行にはそれぞれ二つの整数，底面多角形の頂点の x-座標と y-座標が与えられる． それらは −1000 以上 1000 以下である． 頂点は反時計回り順に並んでいる． 底面の多角形は必ず凸である．

その後にまったく同様にもう一方の製品の底面多角形の記述が与えられる．

入力の終わりは，ゼロだけからなる行で表される．

各データセットについて，二つの製品が同時に収まるキャニスタの底面円の直径の最小値を一行に出力せよ． 出力は 10⁻⁶ を超える誤差を含んではならない．

3
8 0
7 7
0 6
4
0 0
5 0
5 5
0 5
3
0 0
2 2
0 2
3
3 1
5 1
5 3
5
0 0
3 0
3 1
1 3
0 3
5
0 0
3 0
3 1
1 3
0 3
9
0 0
9 4
13 13
9 22
6 24
-6 24
-9 22
-13 13
-9 4
4
1 0
0 5
-1 0
0 -5
0

10.625000000000
2.828427124746
5.656854249492
26.000000000000