In the 17th century, Fermat wrote that he proved for any integer
![]() ,
there exist no positive integers x, y, z such that
,
there exist no positive integers x, y, z such that
![]() .
However he never disclosed the proof. Later, this claim was named
Fermat's Last Theorem or Fermat's Conjecture.
.
However he never disclosed the proof. Later, this claim was named
Fermat's Last Theorem or Fermat's Conjecture.
If Fermat's Last Theorem holds in case of n, then it also holds in case of any multiple of n. Thus it suffices to prove cases where n is a prime number and the special case n = 4.
A proof for the case n = 4 was found in Fermat's own memorandum. The case n = 3 was proved by Euler in the 18th century. After that, many mathematicians attacked Fermat's Last Theorem. Some of them proved some part of the theorem, which was a partial success. Many others obtained nothing. It was a long history. Finally, Wiles proved Fermat's Last Theorem in 1994.
Fermat's Last Theorem implies that for any integers
![]() and z > 1, it always holds that
and z > 1, it always holds that
Your mission is to write a program that verifies this in the case n = 3 for a given z. Your program should read in integer numbers greater than 1, and, corresponding to each input z, it should output the following:
for the corresponding input integer z. No other characters should appear in any output line.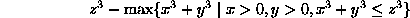
6 4 2 0
27 10 6