くるくる
2次元平面上の多角形の壁の内側を,時計回りに回転する棒を考える(図1参照).
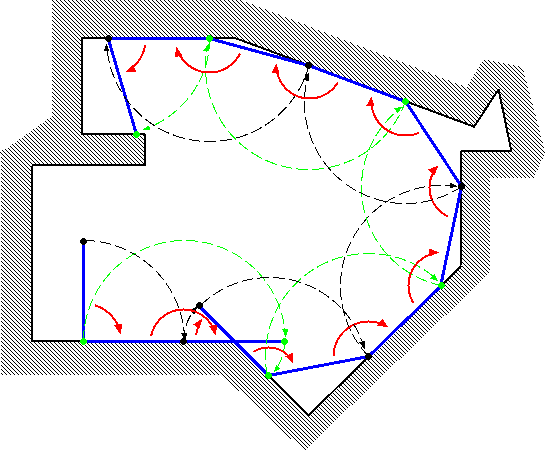
図1. 多角形の内側で回転する棒
最初は棒の片端(A端と呼ぶ)が(0,0),他端(B端と呼ぶ)が(0,L)にある.
Lは棒の長さである.棒は最初はA端のみで壁に接している.
棒は壁に接している点を中心にして回転する.
新たな点が壁に接すると,回転の中心も変わる.
あなたの仕事は棒が与えられた回数Rだけ回転し終わった時点での
A端の座標を計算することである.
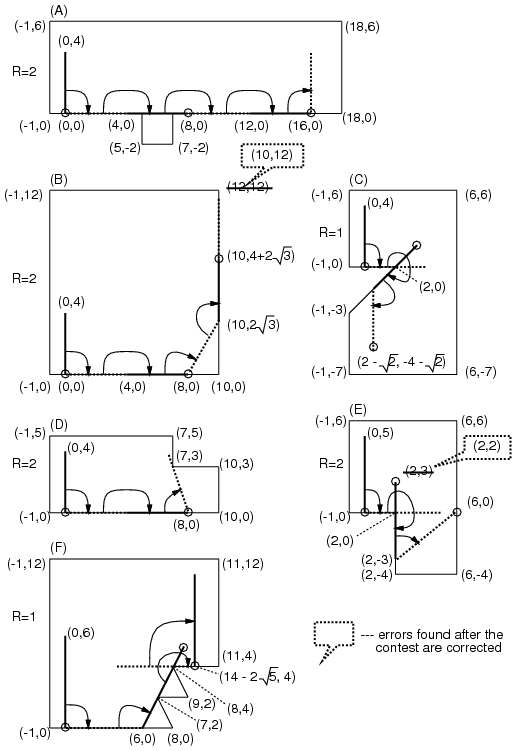
図2. 棒の回転のさまざまな例
図2にいくつかの例を示す.(D)と(E)では,棒は途中でつかえた
(壁に接しているいずれの点を中心としても,それ以上時計回りに回転できない) 状態となる.そのような場合は,
その (つかえた) 状態でのA端の座標を出力すること.
以下のことを前提としてよい:
棒の長さ L が ε (|ε| < 0.00001) だけ変化したとき,
結果の(x,y)座標が 0.0005 より大きく変化することはない.
Input
入力は複数のデータセットから成る.データセットの個数は100以下である.
入力の終わりは「0 0 0」で示される.
各データセットは以下の形式で与えられる:
L R N
X1 Y1
X2 Y2
...
XN YN
Lは棒の長さである.棒は,途中ではつかえない場合,
2π×R ラジアン回転する.Nは多角形を構成する頂点の個数である.
多角形の頂点は,反時計回りの順番で並べられている.
多角形は単純であると仮定して構わない.
すなわち,多角形の外周が自分自身と接触ないし交差することはない.
N, Xi, Yi は整数で,
その他の値は十進小数である.それらの値の範囲は次の通り:
1.0 ≤ L ≤ 500.0,
1.0 ≤ R ≤ 10.0,
3 ≤ N ≤ 100,
-1000 ≤ Xi ≤ 1000,
-1000 ≤ Yi ≤ 1000,
X1 ≤ -1, Y1 = 0,
X2 ≥ 1, Y2 = 0.
Output
それぞれのデータセットに対して,A端の最終状態におけるx座標とy座標を,
スペース1個で区切った1行として出力すること.
出力する値は0.001以下の誤差を含んでいても構わない.
また,値は小数点以下何桁表示しても構わない.
Sample Input
4.0 2.0 8
-1 0
5 0
5 -2
7 -2
7 0
18 0
18 6
-1 6
4.0 2.0 4
-1 0
10 0
10 12
-1 12
4.0 1.0 7
-1 0
2 0
-1 -3
-1 -8
6 -8
6 6
-1 6
4.0 2.0 6
-1 0
10 0
10 3
7 3
7 5
-1 5
5.0 2.0 6
-1 0
2 0
2 -4
6 -4
6 6
-1 6
6.0 1.0 8
-1 0
8 0
7 2
9 2
8 4
11 4
11 12
-1 12
0 0 0
Output for the Sample Input
16.0 0.0
9.999999999999998 7.4641016151377535
0.585786437626906 -5.414213562373095
8.0 0.0
6.0 0.0
9.52786404500042 4.0
なお,上記のサンプル入力は図2の各ケースに対応している.
また,図3にケース(C)の様子を示すアニメーションと分解写真を示す.

図3. ケース(C)に対するアニメーションと分解写真











