(コンテストの後でみつかった誤記を修正)

著名な生物学者である部陪博士は生物が発生段階でどのようにして左右非対称になるかに関する研究を続けた結果，一つの仮説に至った．その仮説を学会で発表するため，部陪博士は一つの細胞が分裂を繰り返していく過程を木の形に表した図をポスターに印刷することにした．あなたの仕事は，教授から受け取った木のデータを，聴衆が理解しやすいように，ある決められた条件を満たす形に整形するプログラムを作成することである．

細胞の分裂過程を表す木は次のような形状をしている．

• 一番上に，出発点となる細胞を表す丸がある．
• 細胞は「それ以上分裂しない」か「二つの子細胞に分裂する」かのどちらかなので，各細胞を表す丸からは「下に向かう枝が全く出ていない」か，あるいは，「2個の子細胞への2本の枝が下に伸びている」かのどちらかである．

次に，そのような木の例を示す．

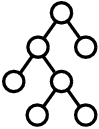
図 F-1: 細胞の分裂過程を表す木

博士の仮説によれば，この木の構造を見れば，その中に現れる各細胞の「非対称性の強さ」を比較できるという．そのような比較を行うための準備として，まず各細胞の「左右類似度」と呼ばれる値が次のようにして定義される．

1. それ以上，分裂しなかった細胞の左右類似度は 0 である．
2. 二つに分裂した細胞の左右類似度は，その二つの子細胞およびその子孫細胞の各々を出発点とする部分的な木として何種類の構造が現れるかを考え，それらのうちの左の子細胞側と右の子細胞側の双方に共通に現れているものの割合で与えられる．なお，二つの木が，任意の適当な細胞に対してその左右の子細胞を入れ替えることで全く同じ形にできる場合は，この二つの木は同じ構造を持つとみなす．

例えば，次のような木を考える．

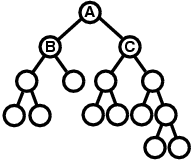
図 F-2: 木の例

この木における細胞 A の左右類似度は次のように求められる．まず，A の左の子細胞である B 以下に現れる木には，構造としては次の 3 種類のものがある．右端に描かれた構造を持つ木は 3 回現れるが，構造としては 1 種類と数える．

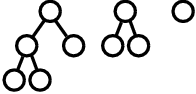
図 F-3: 細胞 B 以下に現れる構造

一方，A の右の子細胞である C 以下には，次の 4 種類の構造が現れる．

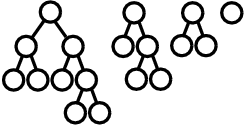
図 F-4: 細胞 C 以下に現れる構造

これらのうち，B 以下の構造の 1，2，3 番目のものは，それぞれ，C 以下の構造の 2，3，4 番目のものと同じ構造とみなされる．よって，計 4 種類の構造が現れていて，そのうち，左右共通に現れているのは 3 種類ということになり，細胞 A の左右類似度は 3/4 である．

博士の仮説によれば，この「左右類似度」を用いて，二つの細胞 X と Y のどちらがより「非対称性が強い」かを以下の規則に基づいて判定できる．

1. X と Y の左右類似度が異なる場合は，左右類似度が低い方が非対称性が強い．
2. そうでない場合で，X と Y の双方に子細胞がない場合は，非対称性の強さは全く等しい．
3. そうでない場合は，X と Y の双方に二つの子細胞があるはずなので，X の子細胞のうちの非対称性が強い(または等しい)方と Y の子細胞のうちの非対称性が強い(または等しい)方とを比較し，より非対称性が強い子細胞を持っている方が，非対称性が強い．
4. それでも同点の場合は，X の子細胞と Y の子細胞のうち，もう一方の非対称性が弱い(または等しい)方同士を比較し，より非対称性が強い子細胞を持っている方が，非対称性が強い．
5. それでも同点の場合は， X と Y の非対称性は全く等しい．

また，上記規則群の中で子細胞同士の非対称性の強さを比較する場合は，再帰的に上記規則群を適用するものとする．

さて，今回作成するのは，細胞の分裂過程を表す前述のような木構造が与えられた際に，各細胞の左の子細胞と右の子細胞を適宜，入れ替えていくことによって，次のような条件が満たされている状態に整形するプログラムである．

1. 与えられた木全体の出発点となっているか，または，親細胞の左の子細胞となっている全ての細胞 X について，もし X が二つの子細胞を持つ場合は，それら二つの子細胞のうち，より非対称性が強い(または等しい)方が X の左の子細胞になっている．
2. 親細胞の右の子細胞となっている全ての細胞 X について，もし X が二つの子細胞を持つ場合は，それら二つの子細胞のうち，より非対称性が強い(または等しい)方が X の右の子細胞になっている．

なお，二つの子細胞の非対称性が等しい場合は，どちらを左に配置しても同じ形の木になるので，順番は任意であるものとする．

例えば，図F-2 の木の場合，B と C を比較すると B の方が左右類似度が低く，そのため非対称性が強いので，B が左，C が右という配置は変わらない．さらに，B が A の「左の子細胞」であるので，B の子細胞のうち非対称性が強いものが左へ配置される．逆に，C は A の「右の子細胞」であるので，C の子細胞のうち非対称性が強いものが右へ配置される．他の細胞に対しても同様に考えていくと，最終的な整形結果は次のようになる．

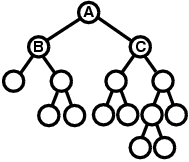
図 F-5: 整形結果の例

なお，与えられた木に対して行って良い操作は同じ親の左右の子細胞の入れ替えのみであることに注意すること．例えば，図F-2の木を以下のように変形することはできない．

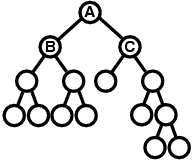
図 F-6: 許されない操作の例

入力は，n個(1≤n≤100)の木を記述しているn行と，それに続く，入力の終わりを表す一つの「0」のみからなる行とからなる．一つの木は最小1個最大127個の細胞を含む．各木を表す記述は，たとえば，次のような形式をしている．

((x (x x)) x)

これは，図F-1に示した木を表現している．より形式的には，木の記述は，

"(" <左の子細胞以下の木の記述> <一つのスペース> <右の子細胞以下の木の記述> ")"

または，

"x"

のどちらかの形式を取る．前者が出発点となる細胞に子細胞が二つある木の記述形式，後者が出発点となる細胞に子細胞がない木の記述形式である．

出力には，入力の各木に対してその整形結果一つを 1 行に出力せよ．出力の順番は，対応する入力中の木と同じ順番であること．木の記述には入力と同じ記述形式を用いること．また，各行は，一つの木の記述以外に余計な文字を含んではならない．

(((x x) x) ((x x) (x (x x))))
(((x x) (x x)) ((x x) ((x x) (x x))))
(((x x) ((x x) x)) (((x (x x)) x) (x x)))
(((x x) x) ((x x) (((((x x) x) x) x) x)))
(((x x) x) ((x (x x)) (x (x x))))
((((x (x x)) x) (x ((x x) x))) ((x (x x)) (x x)))
((((x x) x) ((x x) (x (x x)))) (((x x) (x x)) ((x x) ((x x) (x x)))))
0

((x (x x)) ((x x) ((x x) x)))
(((x x) ((x x) (x x))) ((x x) (x x)))
(((x ((x x) x)) (x x)) ((x x) ((x x) x)))
(((x ((x ((x x) x)) x)) (x x)) ((x x) x))
((x (x x)) ((x (x x)) ((x x) x)))
(((x (x x)) (x x)) ((x ((x x) x)) ((x (x x)) x)))
(((x (x x)) ((x x) ((x x) x))) (((x x) (x x)) (((x x) (x x)) (x x))))