Links
Problem A
等しい合計点
太郎と花子はそれぞれカードを何枚か持っている. 各カードには点数が書かれている. 太郎のカードと花子のカードを 1 枚ずつ交換して, それぞれの持つカードの合計点数が等しくなるようにしたい. どのカードとどのカードを交換したらよいか.
ただし,カードを交換しなくても合計点数が等しい場合でも, 必ずカードの交換を行うものとする.
Input
入力は,いくつかのデータセットからなる. 各データセットは次の形式で与えられる.
n m
s1
s2
...
sn
sn+1
sn+2
...
sn+m
各データセットの最初の行は空白ひとつで区切られたふたつの数 n と m を含み, n は太郎のカードの枚数,m は花子のカードの枚数を表す. 続く n+m 行には,各カードの点数が 1 行にひとつずつ並ぶ. 最初の n 個の点数 (s1 から sn まで) は太郎のカードの点数, 残りの m 個の点数 (sn+1 から sn+m まで) は花子のカードの点数を表す.
n および m は 100 以下の正の整数とし, カードの点数は 0 以上 100 以下の整数値とする.
入力の終わりは,空白ひとつで区切られたふたつの 0 を含む 1 行で示される.
Output
各データセットに対し, ふたつの数を 1 行にひとつの空白で区切って出力せよ. 最初の数は太郎が花子に渡すカードの点数, 2 番目の数は花子が太郎に渡すカードの点数である. なお,合計を等しくするようなカードの交換の方法が複数ある場合は, 交換するカードの点数の和が最小となるものを出力すること.
カードの点数の合計を等しくするような交換が存在しない場合は -1 のみを含む 1 行を出力すること. 出力形式に従わない余計な文字を含んではならない.
Sample Input
2 2 1 5 3 7 6 5 3 9 5 2 3 3 12 2 7 3 5 4 5 10 0 3 8 1 9 6 0 6 7 4 1 1 2 1 2 1 4 2 3 4 3 2 3 1 1 2 2 2 0 0
Output for the Sample Input
1 3 3 5 -1 2 2 -1
Problem B
月曜土曜素因数
審判長日誌,宇宙暦 48642.5. われわれは,初等整数論から出題することに決めた. 正整数の素因数をすべて求めることに似た問題だが, そうではない.
7 で割った余りが 1 または 6 である正整数は 7N+{1,6} 数と呼ばれる. しかし,発音しにくいので, 月曜土曜数と呼ぼう.
月曜土曜数 a, b に対して, 月曜土曜数 x が存在して ax = b が成り立つとき, a を b の月曜土曜約数と呼ぶ. 月曜土曜数 a が月曜土曜数 b の月曜土曜約数であるためには, a が b の普通の意味の約数であれば必要十分であると, 簡単に証明できる.
1 より大きな月曜土曜数でそれ自身と 1 の他に月曜土曜約数をもたないものを, 月曜土曜素数と呼ぶ. 普通の意味の素数である月曜土曜数は月曜土曜素数であるが, 逆は一般に成り立たない. たとえば,27 は普通の意味の素数ではないが,月曜土曜素数である. 月曜土曜数 a の月曜土曜約数である月曜土曜素数を, a の月曜土曜素因数と呼ぶ. たとえば, 27 は月曜土曜素数であり, 216 = 27 × 8 が成り立つので, 27 は 216 の月曜土曜素因数のひとつである.
1 より大きなどんな月曜土曜数も, 1 個以上の月曜土曜素数の積として表すことができる. 表し方は,順序の違いを無視しても,必ずしも一通りではない. たとえば, 216 = 6 × 6 × 6 = 8 × 27 である.
選手は, 入力された各々の月曜土曜数に対して, その月曜土曜素因数をすべて出力するプログラムを書かなくてはならない.
Input
入力は行の並びで,各行に一つの月曜土曜数が含まれている.
各々の月曜土曜数は 1 より大きく 300000 (三十万)より小さい.
入力の終わりは,数字 1 が 1 文字だけ含まれる行で示される.
Output
入力された月曜土曜数それぞれに対して, その数が表示され,つづけて同じ行に, コロン「:」,そして,月曜土曜素因数の並びがそれぞれの前に空白を置いて 小さい順に出力されなくてはならない. 各月曜土曜素因数は,たとえ入力された月曜土曜数を 2 回以上割るものであっても, ちょうど 1 回だけ出力されなくてはならない.
Sample Input
205920 262144 262200 279936 299998 1
Output for the Sample Input
205920: 6 8 13 15 20 22 55 99 262144: 8 262200: 6 8 15 20 50 57 69 76 92 190 230 475 575 874 2185 279936: 6 8 27 299998: 299998
Problem C
如何に汝を満足せしめむ? いざ数え上げむ…
三値論理は値として "真","偽" に加え "未知" を許す論理体系である. 以下では,"偽","未知","真" を 0, 1, 2 でそれぞれ表す.
"-" を単項演算子(すなわち,値ひとつを受け取る関数を表す記号)とし, "*" と "+" を二項演算子(すなわち,値ふたつを受け取る関数を表す記号)とする. これらは,それぞれ否定 (NOT), 論理積 (AND), 論理和 (OR) を表す演算子であり, 三値論理におけるこれらの演算は表 C-1 に示すように定義できる.
| -X | (X*Y) | (X+Y) | |||
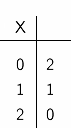 | 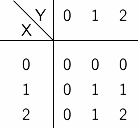 | 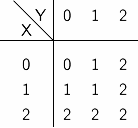 |
P, Q, R を三値論理の変数とする. 与えられた論理式を満足する, つまり論理式の値が 2 になるような (P,Q,R) の三つ組が何通りあるかを答えるのがあなたの役割だ. 論理式は以下のいずれかの形式である(ここで X, Y はまた論理式であるとする).
- 定数: 0, 1 または 2
- 変数: P, Q または R
- 否定: -X
- 論理積: (X*Y)
- 論理和: (X+Y)
たとえば,入力 (P*Q) に対しては,(P,Q,R) が (2,2,0),(2,2,1),(2,2,2) の場合, かつその場合のみ,この論理式の値が 2となるので,3を出力すればよい.
Input
入力は ひとつ以上の行からなり,入力の各行は論理式ひとつを含む. 論理式は 0, 1, 2, P, Q, R, -, *, +, (, ) から成る文字列であり, 空白など他の文字を含まない.論理式の文法は次の BNF で与えられる.
<formula> ::= 0 | 1 | 2 | P | Q | R |
-<formula> | (<formula>*<formula>) | (<formula>+<formula>)
すべての論理式はこの構文規則に従うので,文法エラーを気にする必要はない. 入力行の長さは 80文字を超えない.
入力の終わりは "."(ピリオド)ひとつだけからなる行によって示される.
Output
入力の論理式の値を 2 とするような (P,Q,R) の三つ組の個数を十進数で出力せよ. 出力は論理式ひとつごとに 1 行とし, 各行は個数を表す十進数以外の文字を含んではならない.
Sample Input
(P*Q) (--R+(P*Q)) (P*-P) 2 1 (-1+(((---P+Q)*(--Q+---R))*(-R+-P))) .
Output for the Sample Input
3 11 0 27 0 7
Problem D
ちょろちょろロボット
ロボットを使ったゲームをしよう. ロボットが 1 台,マス目状に区切られた長方形の盤面上に置かれている(図 D-1). ロボットは,最初北西隅にあるスタート地点のマスに東方向を向いて配置されている. ゲームの目的は,ロボットを南東隅にあるゴールのマスまで誘導することである.
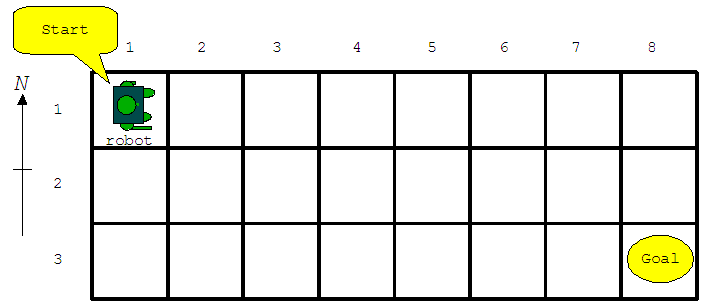
図 D-1: 盤面の例
ロボットは,次の 5 種類の命令を実行することができる.
- 「直進 (Straight)」:
- 現在の進行方向のまま,次のマスに前進する.
- 「右折 (Right)」:
- 進行方向を 90 度右に変えて,次のマスに前進する.
- 「反転 (Back)」:
- 進行方向を 180 度変えて,次のマスに前進する.
- 「左折 (Left)」:
- 進行方向を 90 度左に変えて,次のマスに前進する.
- 「停止 (Halt)」:
- 現在のマスで止まって,ゲームを終了する.
各マスには,上述の命令のいずれかが割り当てられている(例:図 D-2). 代わりに実行すべき別の命令をプレイヤーが与えない限り, ロボットは,現在いるマスの命令を実行する. プレイヤーが明示的に命令を与える際は,その都度, 命令の種類に応じたコストを支払う必要がある.
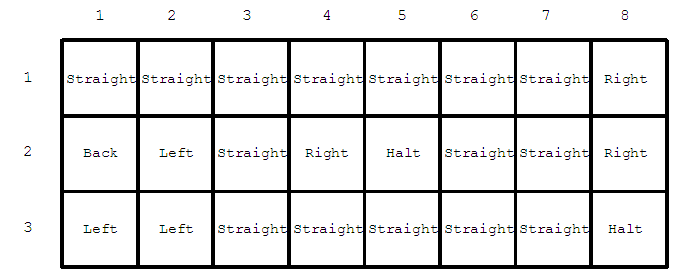
図 D-2: 各マスに割り当てられた命令の例
ロボットは,同じ場所を何度も訪れることが許されている. 一方で,ロボットが盤面外に前進するような命令を実行した場合や, ゴールに着く前に停止命令を実行した場合は,失格となる.
あなたの仕事は, ロボットをスタート地点からゴール地点に誘導するために必要な最小コストを求めるプログラムを書くことである.
Input
入力は,複数のデータセットからなり, 入力の終わりはスペースで区切られたゼロ 2 つからなる行である. 各データセットは,次の形式をしている.
w h
s(1,1) ... s(1,w)
s(2,1) ... s(2,w)
...
s(h,1) ... s(h,w)
c0 c1 c2 c3
h と w は,それぞれ盤面の行および列の数を示す整数であり, 2 ≤ h ≤ 30, 2 ≤ w ≤ 30 と仮定してよい. 続く h 行はそれぞれ,スペースで区切られた w 個の文字から構成されており, 文字 s(i, j) は, i 行 j 列目に位置するマスに割り当てられた命令を示す. その意味は,以下の通り.
- 0: 「直進」命令
- 1: 「右折」命令
- 2: 「反転」命令
- 3: 「左折」命令
- 4: 「停止」命令
ゴールのマス目には,「停止」命令が割り当てられているが, 他のマス目にも「停止」命令が割り当てられていることがあるので,注意せよ.
データセットの最後の行は,スペースで区切られた c0, c1, c2, c3 の 4 つの整数値を含んでおり, それぞれ,「直進」,「右折」,「反転」,「左折」命令を与える際に, プレイヤーが支払うべきコストを示している. プレイヤーが「停止」命令を与えることはできない. また, c0, c1, c2, c3 の値は, 1 以上 9 以下と仮定してよい.
Output
各データセットについて,ロボットをゴールに誘導するために必要な最小コストを求め, 十進数の整数としてそれぞれ 1 行に出力しなさい. 出力行には他の文字があってはならない.
Sample Input
8 3 0 0 0 0 0 0 0 1 2 3 0 1 4 0 0 1 3 3 0 0 0 0 0 4 9 9 1 9 4 4 3 3 4 0 1 2 4 4 1 1 1 0 0 2 4 4 8 7 2 1 2 8 2 2 4 1 0 4 1 3 1 0 2 1 0 3 1 4 1 9 3 1 0 0
Output for the Sample Input
1 11 6
Problem E
大玉転がし
ACM 大学では毎年 7 月に運動会が開かれるが, そのハイライトとなる競技は大玉転がしである. この大玉転がしではグラウンド上にひかれた直線状のコースに沿って大玉を転がす. グラウンドには複数の直方体ブロックが障害物として置かれていて動かすことができない. ブロックに大玉がぶつからないように, かつ大玉の底の点がコースの線から離れないように転がさなければならない.
競技をおもしろくするために,大玉をなるべく大きなものにすることになった. 上の条件を満たすような転がし方が可能な大玉の半径の最大値を求めるプログラムを作成しなさい.
大玉は完全な球,グラウンドは平面とする. ブロックの形は直方体である.ブロックの底面の四辺はグラウンド上にあり, X, Y 軸のいずれかと平行になっている. コースは,始点から終点までの線分として与えられる. 大玉の底の点が始点に接している状態からスタートし, 終点に接している状態でゴールするものとする.
なお,大玉とブロックの位置関係は,図 E-1 (a), (b) のようになる可能性がある.
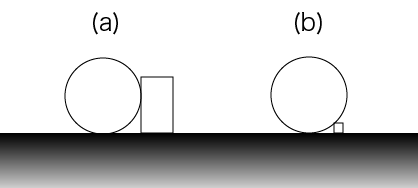
図 E-1: 大玉とブロックの位置関係
Input
入力は,いくつかのデータセットからなる. 各データセットは以下の形式で与えられる.
N
sx sy ex ey
minx1 miny1 maxx1 maxy1 h1
minx2 miny2 maxx2 maxy2 h2
...
minxN minyN maxxN maxyN hN
データセットの最初の行はブロックの数を表す整数 N (1 ≤ N ≤ 50) からなる.次の行は空白ひとつで区切られたよっつの整数からなり, 始点の座標 (sx, sy),終点の座標 (ex, ey) を表す. 続く N 行はそれぞれ空白ひとつで区切られたいつつの整数からなる. 1 行がひとつのブロックに対応し,ブロックの底面の 2 頂点 (minx, miny), (maxx, maxy) と高さ h を表す. 整数 sx, sy, ex, ey, minx, miny, maxx, maxy, h は以下の条件を満たすものとする.
-10000 ≤ sx, sy, ex, ey ≤ 10000
-10000 ≤ minxi < maxxi ≤ 10000
-10000 ≤ minyi < maxyi ≤ 10000
1 ≤ hi ≤ 1000
入力の終わりはゼロひとつの行で示される.
Output
入力データセットごとに大玉の半径の最大値を表す実数を 1 行出力せよ.なお, 与えられたデータセットに対して,半径の最大値が 1000 を超えることはないと仮定してよい.また,コースの線の上にブロックがある場合の, 大玉の半径の最大値は 0 とする.出力する値は 0.001 以下の誤差を含んでいても構わない.値は小数点以下何桁表示しても構わない.
Sample Input
2 -40 -40 100 30 -100 -100 -50 -30 1 30 -70 90 -30 10 2 -4 -4 10 3 -10 -10 -5 -3 1 3 -7 9 -3 1 2 -40 -40 100 30 -100 -100 -50 -30 3 30 -70 90 -30 10 2 -400 -400 1000 300 -800 -800 -500 -300 7 300 -700 900 -300 20 3 20 70 150 70 0 0 50 50 4 40 100 60 120 8 130 80 200 200 1 3 20 70 150 70 0 0 50 50 4 40 100 60 120 10 130 80 200 200 1 3 20 70 150 70 0 0 50 50 10 40 100 60 120 10 130 80 200 200 3 1 2 4 8 8 0 0 10 10 1 1 1 4 9 9 2 2 7 7 1 0
Output for the Sample Input
30 1 18.16666666667 717.7857142857 50.5 50 18.16666666667 0 0
Problem F
ICPC: チョコレートの知的合同分割
双子の達也と和也はチョコレートが大好きである. かれらは大好物の板チョコレートを見つけたがそれはずいぶん変な形をしていた. ママの食べかけらしい. もちろん, 彼らはそれを食べる権利を主張し, 板チョコレートを切って二つのかけらにしてそれぞれの分け前とすることにした. チョコレートが公平に分割されたことを確信するために, 彼らは二つのかけらの形が「合同」であること, および, それぞれのかけらが「連結」していることを要求した.
板チョコレートはたくさんの正方形チョコレートでできており, それらは縁で隣接する正方形チョコレートと連結している. 板チョコレート全体も連結している.
この板チョコレートを正方形の縁に沿って切り, 二つの合同で連結なチョコレートのかけらに分割するのをあなたに手伝って欲しい. すなわち, 適切に回転, 裏返し, 移動することにより, 分割されたかけら同士がぴったり重なるようにするということである.
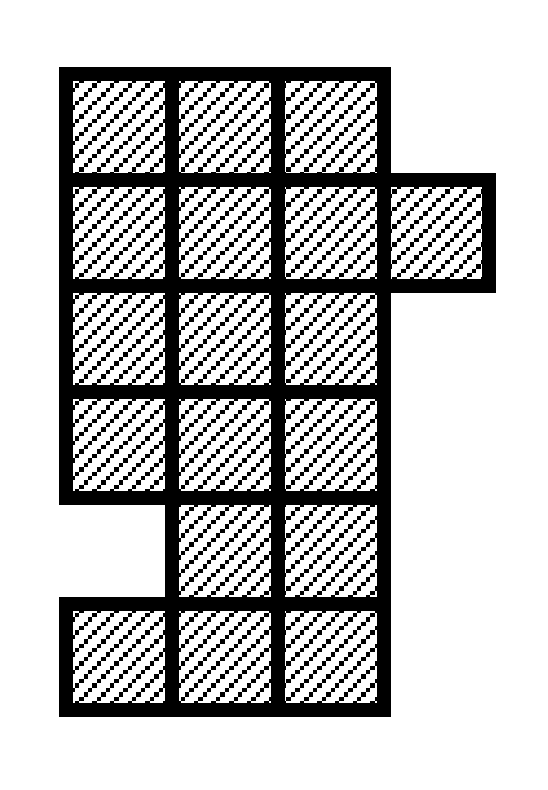
図 F-1: 18 個の正方形チョコレートからなる食べかけ板チョコレート
例として図 F-1 のような 18 個の正方形チョコレートからなる食べかけ板チョコレートを考える. これを正方形の縁に沿って切り, 図 F-2 のように, 9 個ずつの正方形からなる二つのかけらに分ける.
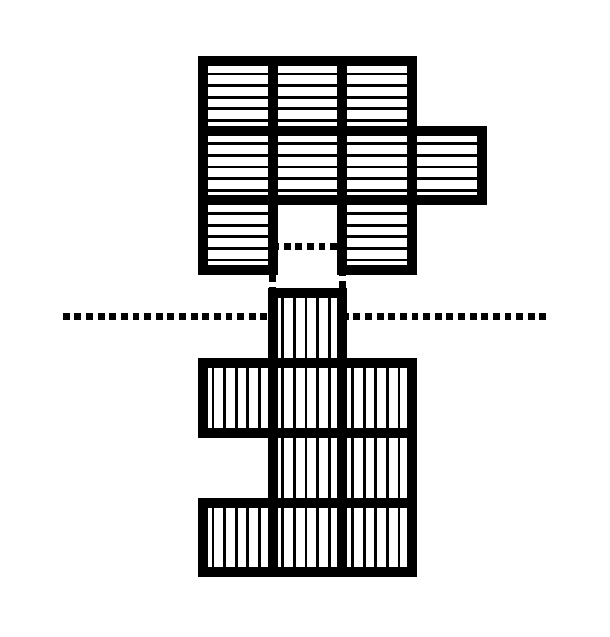
図 F-2: 板チョコレート (図 F-1) の分割
結果として, 二つの合同で連結なかけらが得られる. そのうちの一つは横縞模様の正方形 9 個からなり, もう一方は縦縞模様からなる. 上のかけらは, 時計回りに 90 度回転させて水平線を軸に裏返すと, 下のかけらにぴったり重なる.
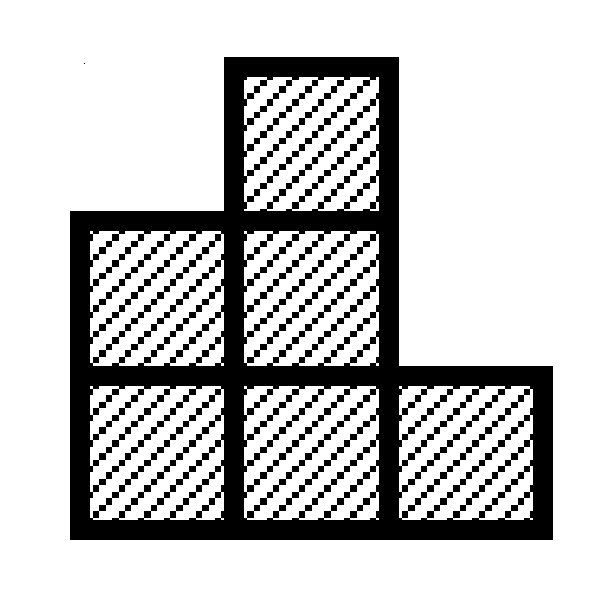
図 F-3: 合同で連結な二つのかけらに分割できない図形
角でだけ接触している二つの正方形は連結していないとみなされる. 図 F-3 は合同で連結な二つのかけらに分割できない形の例である. 連結でなくてよければ, この形は 3 個の正方形からなる合同なかけらに 2 分割できることに 注意されたい (図 F-4).

図 F-4: 合同だが連結ではない二つのかけら
あなたの仕事は, 与えられた板チョコレートがこのような合同で連結な二つのかけらに分割できるかどうかを判定するプログラムを書くことである.
Input
入力は,複数のデータセットからなり, 入力の終わりはスペースで区切られたゼロ二つからなる行である. 各データセットは,次の形式をしている.
w h
r(1, 1) ... r(1, w)
r(2, 1) ... r(2, w)
...
r(h, 1) ... r(h, w)
w と h は,それぞれ板チョコレートの幅と高さを示す整数であり, 2 ≤ w ≤ 10, 2 ≤ h ≤ 10 と仮定してよい. 続く h 行はそれぞれ,スペースで区切られた w 個の数字から構成されており, 数字 r(i, j) は, 場所 (i, j) の正方形チョコレートの有無を表す. その意味は,次の通り.
- '0': チョコレートなし (すでに食べられてしまった).
- '1': 正方形チョコレートあり.
最大で 36 個の正方形チョコレートがあること, すなわち, 各データセットにおける正方形チョコレートを表す '1' の個数は最大 36 であることを仮定してよい. また, 各行, 各列には少なくとも 1 個の正方形チョコレートがあることを仮定してよい.
板チョコレート全体は連結と仮定してよい. ママは板チョコレートに穴をあけるような食べ方はしないので, 図 F-5 のような穴のある形の板チョコレートを表すようなデータセットは無いことを仮定してよい.
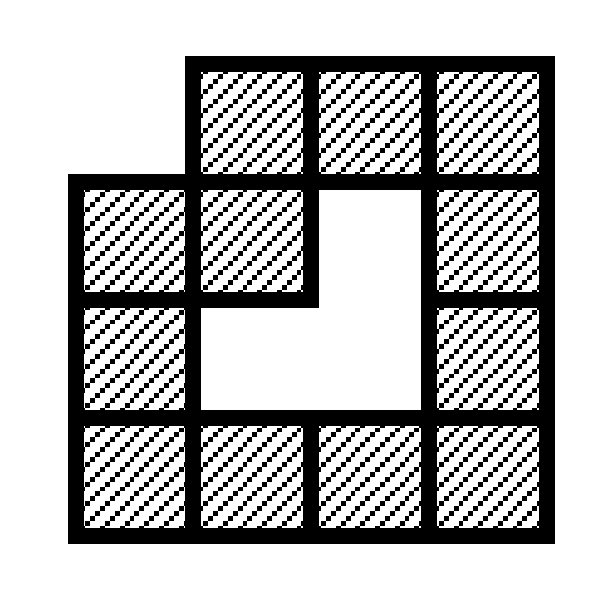
図 F-5: 穴のある形の食べかけ板チョコレート (このようなデータセットは無いと仮定してよい)
Output
出力は,入力データセットごとに "YES" または "NO" の大文字の文字列からなる. "YES" はそのデータセットが表す板チョコレートが 2 個の合同で連結なかけらに分割できることを意味し, "NO" はそのような分割が不可能なことを意味する. 出力行には他の文字があってはならない.
Sample Input
2 2 1 1 1 1 3 3 0 1 0 1 1 0 1 1 1 4 6 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0 0 1 1 0 1 1 1 0 7 5 0 0 1 0 0 1 1 0 1 1 1 1 1 0 0 1 1 1 1 1 0 1 1 1 1 1 1 0 1 0 0 0 1 1 0 9 7 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 9 7 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 7 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 1 1 1 0 10 10 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0
Output for the Sample Input
YES NO YES YES YES NO NO YES
