Links
Problem A
Next Mayor
One of the oddest traditions of the town of Gameston may be that even the town mayor of the next term is chosen according to the result of a game. When the expiration of the term of the mayor approaches, at least three candidates, including the mayor of the time, play a game of pebbles, and the winner will be the next mayor.
The rule of the game of pebbles is as follows. In what follows, n is the number of participating candidates.
- Requisites
- A round table, a bowl, and plenty of pebbles.
- Start of the Game
- A number of pebbles are put into the bowl; the number is decided by the Administration Commission using some secret stochastic process. All the candidates, numbered from 0 to n-1 sit around the round table, in a counterclockwise order. Initially, the bowl is handed to the serving mayor at the time, who is numbered 0.
- Game Steps
- When a candidate is handed the bowl and if any pebbles are in it, one pebble is taken out of the bowl and is kept, together with those already at hand, if any. If no pebbles are left in the bowl, the candidate puts all the kept pebbles, if any, into the bowl. Then, in either case, the bowl is handed to the next candidate to the right. This step is repeated until the winner is decided.
- End of the Game
- When a candidate takes the last pebble in the bowl, and no other candidates keep any pebbles, the game ends and that candidate with all the pebbles is the winner.
A math teacher of Gameston High, through his analysis, concluded that this game will always end within a finite number of steps, although the number of required steps can be very large.
Input
The input is a sequence of datasets. Each dataset is a line containing two integers n and p separated by a single space. The integer n is the number of the candidates including the current mayor, and the integer p is the total number of the pebbles initially put in the bowl. You may assume 3 ≤ n ≤ 50 and 2 ≤ p ≤ 50.
With the settings given in the input datasets, the game will end within 1000000 (one million) steps.
The end of the input is indicated by a line containing two zeros separated by a single space.
Output
The output should be composed of lines corresponding to input datasets in the same order, each line of which containing the candidate number of the winner. No other characters should appear in the output.
Sample Input
3 2 3 3 3 50 10 29 31 32 50 2 50 50 0 0
Output for the Sample Input
1 0 1 5 30 1 13
Problem B
How Many Islands?
You are given a marine area map that is a mesh of squares, each representing either a land or sea area. Figure B-1 is an example of a map.
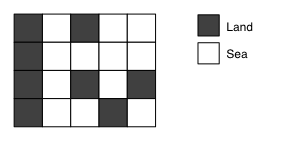
Figure B-1: A marine area map
You can walk from a square land area to another if they are horizontally, vertically, or diagonally adjacent to each other on the map. Two areas are on the same island if and only if you can walk from one to the other possibly through other land areas. The marine area on the map is surrounded by the sea and therefore you cannot go outside of the area on foot.
You are requested to write a program that reads the map and counts the number of islands on it. For instance, the map in Figure B-1 includes three islands.
Input
The input consists of a series of datasets, each being in the following format.
w h
c1,1 c1,2 ... c1,w
c2,1 c2,2 ... c2,w
...
ch,1 ch,2 ... ch,w
w and h are positive integers no more than 50 that represent the width and the height of the given map, respectively. In other words, the map consists of w×h squares of the same size. w and h are separated by a single space.
ci, j is either 0 or 1 and delimited by a single space. If ci, j = 0, the square that is the i-th from the left and j-th from the top on the map represents a sea area. Otherwise, that is, if ci, j = 1, it represents a land area.
The end of the input is indicated by a line containing two zeros separated by a single space.
Output
For each dataset, output the number of the islands in a line. No extra characters should occur in the output.
Sample Input
1 1 0 2 2 0 1 1 0 3 2 1 1 1 1 1 1 5 4 1 0 1 0 0 1 0 0 0 0 1 0 1 0 1 1 0 0 1 0 5 4 1 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 1 5 5 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0
Output for the Sample Input
0 1 1 3 1 9
Problem C
Verbal Arithmetic
Let's think about verbal arithmetic.
The material of this puzzle is a summation of non-negative integers represented in a decimal format, for example, as follows.
905 + 125 = 1030
In verbal arithmetic, every digit appearing in the equation is masked with an alphabetic character. A problem which has the above equation as one of its answers, for example, is the following.
ACM + IBM = ICPC
Solving this puzzle means finding possible digit assignments to the alphabetic characters in the verbal equation.
The rules of this puzzle are the following.
- Each integer in the equation is expressed in terms of one or more digits '0'-'9', but all the digits are masked with some alphabetic characters 'A'-'Z'.
- The same alphabetic character appearing in multiple places of the equation masks the same digit. Moreover, all appearances of the same digit are masked with a single alphabetic character. That is, different alphabetic characters mean different digits.
- The most significant digit must not be '0', except when a zero is expressed as a single digit '0'. That is, expressing numbers as "00" or "0123" is not permitted.
There are 4 different digit assignments for the verbal equation above as shown in the following table.
| Mask | A | B | C | I | M | P |
|---|---|---|---|---|---|---|
| Case 1 | 9 | 2 | 0 | 1 | 5 | 3 |
| Case 2 | 9 | 3 | 0 | 1 | 5 | 4 |
| Case 3 | 9 | 6 | 0 | 1 | 5 | 7 |
| Case 4 | 9 | 7 | 0 | 1 | 5 | 8 |
Your job is to write a program which solves this puzzle.
Input
The input consists of a number of datasets. The end of the input is indicated by a line containing a zero.
The number of datasets is no more than 100. Each dataset is formatted as follows.
N
STRING 1
STRING 2
...
STRING N
The first line of a dataset contains an integer N which is the number of integers appearing in the equation. Each of the following N lines contains a string composed of uppercase alphabetic characters 'A'-'Z' which mean masked digits.
Each dataset expresses the following equation.
STRING 1 + STRING 2 + ... + STRING N -1 = STRING N
The integer N is greater than 2 and less than 13. The length of STRING i is greater than 0 and less than 9. The number of different alphabetic characters appearing in each dataset is greater than 0 and less than 11.
Output
For each dataset, output a single line containing the number of different digit assignments that satisfy the equation.
The output must not contain any superfluous characters.
Sample Input
3 ACM IBM ICPC 3 GAME BEST GAMER 4 A B C AB 3 A B CD 3 ONE TWO THREE 3 TWO THREE FIVE 3 MOV POP DIV 9 A B C D E F G H IJ 0
Output for the Sample Input
4 1 8 30 0 0 0 40320
Problem D
Discrete Speed
Consider car trips in a country where there is no friction. Cars in this country do not have engines. Once a car started to move at a speed, it keeps moving at the same speed. There are acceleration devices on some points on the road, where a car can increase or decrease its speed by 1. It can also keep its speed there. Your job in this problem is to write a program which determines the route with the shortest time to travel from a starting city to a goal city.
There are several cities in the country, and a road network connecting them. Each city has an acceleration device. As mentioned above, if a car arrives at a city at a speed v , it leaves the city at one of v - 1, v , or v + 1. The first road leaving the starting city must be run at the speed 1. Similarly, the last road arriving at the goal city must be run at the speed 1.
The starting city and the goal city are given. The problem is to find the best route which leads to the goal city going through several cities on the road network. When the car arrives at a city, it cannot immediately go back the road it used to reach the city. No U-turns are allowed. Except this constraint, one can choose any route on the road network. It is allowed to visit the same city or use the same road multiple times. The starting city and the goal city may be visited during the trip.
For each road on the network, its distance and speed limit are given. A car must run a road at a speed less than or equal to its speed limit. The time needed to run a road is the distance divided by the speed. The time needed within cities including that for acceleration or deceleration should be ignored.
Input
The input consists of multiple datasets, each in the following format.
n m
s g
x 1 y 1 d 1 c 1
...
xm ym dm cm
Every input item in a dataset is a non-negative integer. Input items in the same line are separated by a space.
The first line gives the size of the road network. n is the number of cities in the network. You can assume that the number of cities is between 2 and 30, inclusive. m is the number of roads between cities, which may be zero.
The second line gives the trip. s is the city index of the starting city. g is the city index of the goal city. s is not equal to g . You can assume that all city indices in a dataset (including the above two) are between 1 and n , inclusive.
The following m lines give the details of roads between cities. The i -th road connects two cities with city indices xi and yi , and has a distance di (1 ≤ i ≤ m ). You can assume that the distance is between 1 and 100, inclusive. The speed limit of the road is specified by ci . You can assume that the speed limit is between 1 and 30, inclusive.
No two roads connect the same pair of cities. A road never connects a city with itself. Each road can be traveled in both directions.
The last dataset is followed by a line containing two zeros (separated by a space).
Output
For each dataset in the input, one line should be output as specified below. An output line should not contain extra characters such as spaces.
If one can travel from the starting city to the goal city, the time needed for the best route (a route with the shortest time) should be printed. The answer should not have an error greater than 0.001. You may output any number of digits after the decimal point, provided that the above accuracy condition is satisfied.
If it is impossible to reach the goal city, the string "unreachable" should be printed. Note that all the letters of "unreachable" are in lowercase.
Sample Input
2 0 1 2 5 4 1 5 1 2 1 1 2 3 2 2 3 4 2 2 4 5 1 1 6 6 1 6 1 2 2 1 2 3 2 1 3 6 2 1 1 4 2 30 4 5 3 30 5 6 2 30 6 7 1 6 1 2 1 30 2 3 1 30 3 1 1 30 3 4 100 30 4 5 1 30 5 6 1 30 6 4 1 30 0 0
Output for the Sample Input
unreachable 4.00000 5.50000 11.25664
Problem E
Cards
There are many blue cards and red cards on the table. For each card, an integer number greater than 1 is printed on its face. The same number may be printed on several cards.
A blue card and a red card can be paired when both of the numbers printed on them have a common divisor greater than 1. There may be more than one red card that can be paired with one blue card. Also, there may be more than one blue card that can be paired with one red card. When a blue card and a red card are chosen and paired, these two cards are removed from the whole cards on the table.
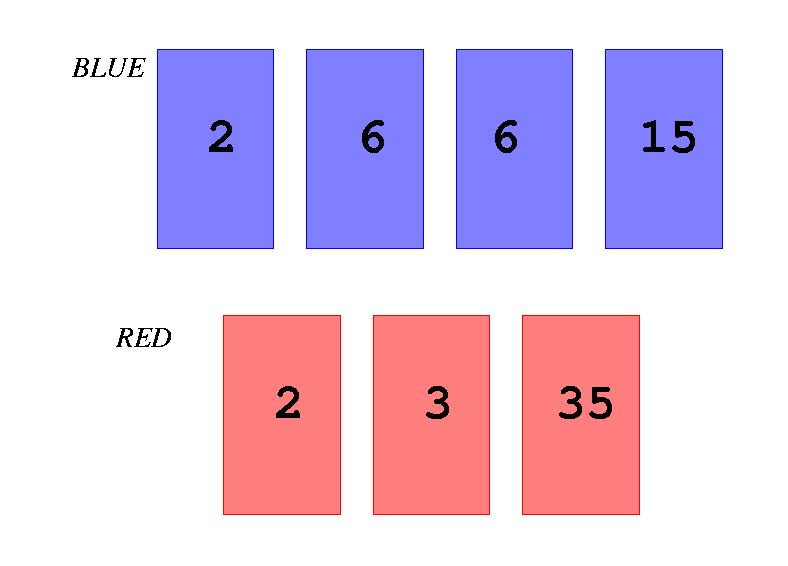
Figure E-1: Four blue cards and three red cards
For example, in Figure E-1, there are four blue cards and three red cards. Numbers 2, 6, 6 and 15 are printed on the faces of the four blue cards, and 2, 3 and 35 are printed on those of the three red cards. Here, you can make pairs of blue cards and red cards as follows. First, the blue card with number 2 on it and the red card with 2 are paired and removed. Second, one of the two blue cards with 6 and the red card with 3 are paired and removed. Finally, the blue card with 15 and the red card with 35 are paired and removed. Thus the number of removed pairs is three.
Note that the total number of the pairs depends on the way of choosing cards to be paired. The blue card with 15 and the red card with 3 might be paired and removed at the beginning. In this case, there are only one more pair that can be removed and the total number of the removed pairs is two.
Your job is to find the largest number of pairs that can be removed from the given set of cards on the table.
Input
The input is a sequence of datasets. The number of the datasets is less than or equal to 100. Each dataset is formatted as follows.
m n
b1 ... bk ... bm
r1 ... rk ... rn
The integers m and n are the number of blue cards and that of red cards, respectively. You may assume 1 ≤ m ≤ 500 and 1≤ n ≤ 500. bk (1 ≤ k ≤ m) and rk (1 ≤ k ≤ n) are numbers printed on the blue cards and the red cards respectively, that are integers greater than or equal to 2 and less than 10000000 (=107). The input integers are separated by a space or a newline. Each of bm and rn is followed by a newline. There are no other characters in the dataset.
The end of the input is indicated by a line containing two zeros separated by a space.
Output
For each dataset, output a line containing an integer that indicates the maximum of the number of the pairs.
Sample Input
4 3 2 6 6 15 2 3 5 2 3 4 9 8 16 32 4 2 4 9 11 13 5 7 5 5 2 3 5 1001 1001 7 11 13 30 30 10 10 2 3 5 7 9 11 13 15 17 29 4 6 10 14 18 22 26 30 34 38 20 20 195 144 903 63 137 513 44 626 75 473 876 421 568 519 755 840 374 368 570 872 363 650 155 265 64 26 426 391 15 421 373 984 564 54 823 477 565 866 879 638 100 100 195 144 903 63 137 513 44 626 75 473 876 421 568 519 755 840 374 368 570 872 363 650 155 265 64 26 426 391 15 421 373 984 564 54 823 477 565 866 879 638 117 755 835 683 52 369 302 424 513 870 75 874 299 228 140 361 30 342 750 819 761 123 804 325 952 405 578 517 49 457 932 941 988 767 624 41 912 702 241 426 351 92 300 648 318 216 785 347 556 535 166 318 434 746 419 386 928 996 680 975 231 390 916 220 933 319 37 846 797 54 272 924 145 348 350 239 563 135 362 119 446 305 213 879 51 631 43 755 405 499 509 412 887 203 408 821 298 443 445 96 274 715 796 417 839 147 654 402 280 17 298 725 98 287 382 923 694 201 679 99 699 188 288 364 389 694 185 464 138 406 558 188 897 354 603 737 277 35 139 556 826 213 59 922 499 217 846 193 416 525 69 115 489 355 256 654 49 439 118 961 0 0
Output for the Sample Input
3 1 0 4 9 18 85
Problem F
Tighten Up!
We have a flat panel with two holes. Pins are nailed on its surface. From the back of the panel, a string comes out through one of the holes to the surface. The string is then laid on the surface in a form of a polygonal chain, and goes out to the panel's back through the other hole. Initially, the string does not touch any pins.
Figures F-1, F-2, and F-3 show three example layouts of holes, pins and strings. In each layout, white squares and circles denote holes and pins, respectively. A polygonal chain of solid segments denotes the string.
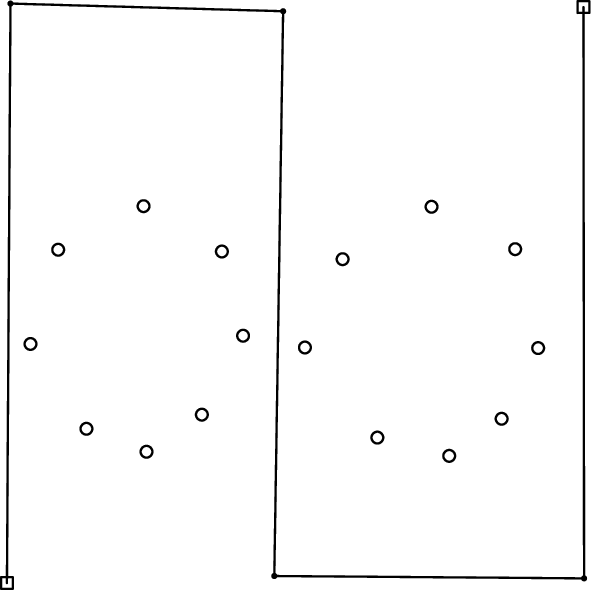
Figure F-1: An example layout of holes, pins and a string
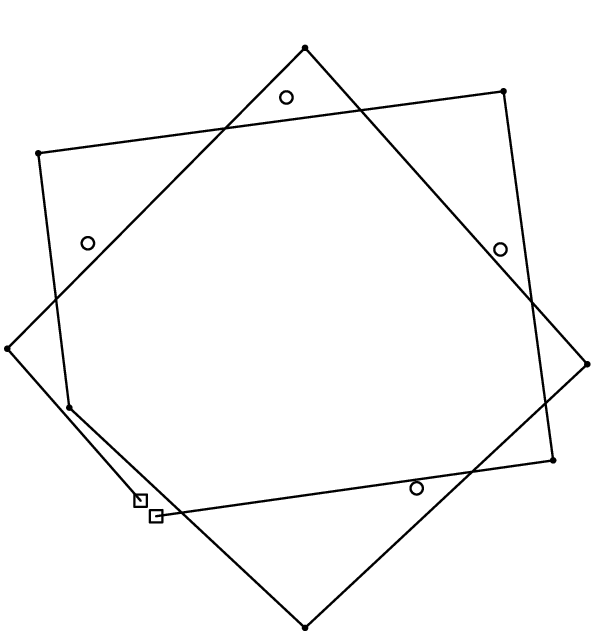
Figure F-2: An example layout of holes, pins and a string
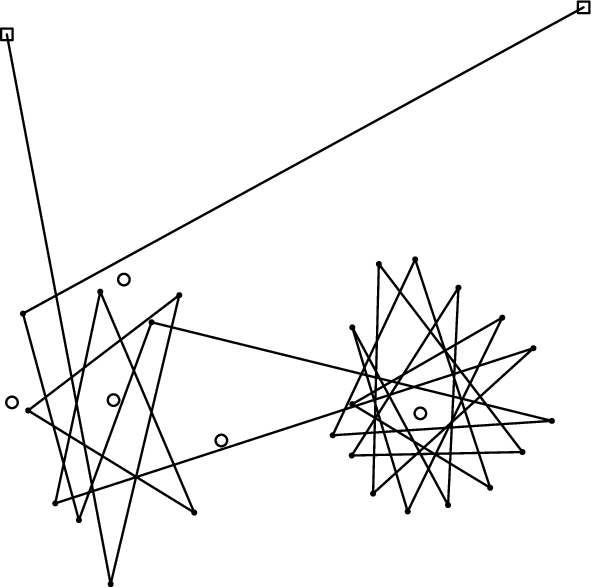
Figure F-3: An example layout of holes, pins and a string
When we tie a pair of equal weight stones to the both ends of the string, the stones slowly straighten the string until there is no loose part. The string eventually forms a different polygonal chain as it is obstructed by some of the pins. (There are also cases when the string is obstructed by no pins, though.)
The string does not hook itself while being straightened. A fully tightened string thus draws a polygonal chain on the surface of the panel, whose vertices are the positions of some pins with the end vertices at the two holes. The layouts in Figures F-1, F-2, and F-3 result in the respective polygonal chains in Figures F-4, F-5, and F-6. Write a program that calculates the length of the tightened polygonal chain.
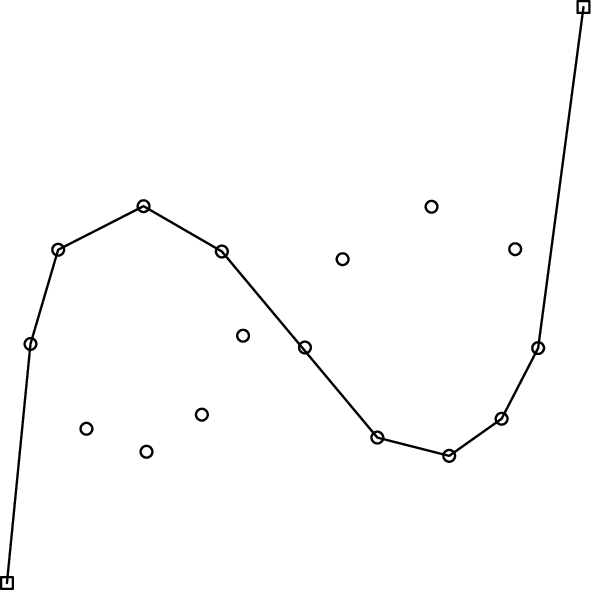
Figure F-4: Tightened polygonal chains from the example in Figure F-1.
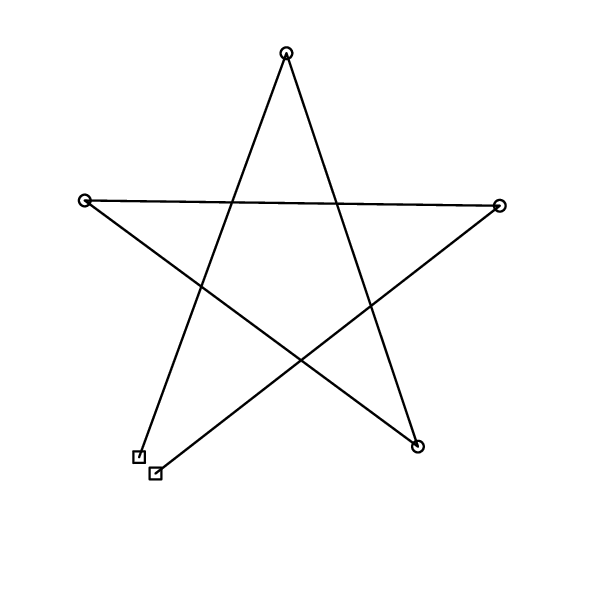
Figure F-5: Tightened polygonal chains from the example in Figure F-2.
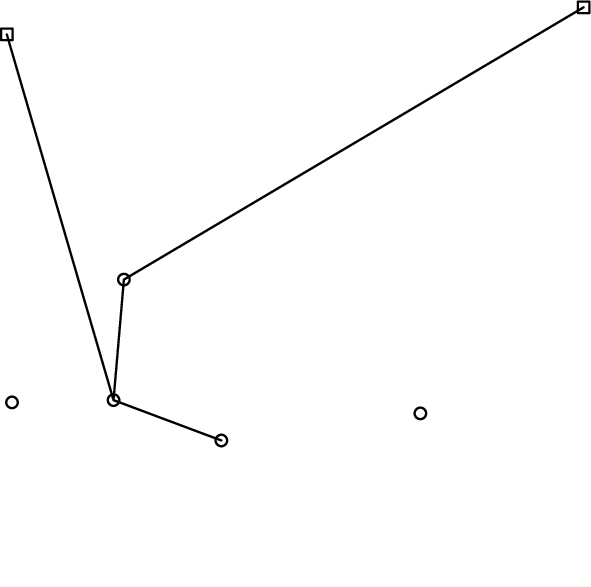
Figure F-6: Tightened polygonal chains from the example in Figure F-3.
Note that the strings, pins and holes are thin enough so that you can ignore their diameters.
Input
The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset gives the initial shape of the string (i.e., the positions of holes and vertices) and the positions of pins in the following format.
m n
x1 y1
...
xl yl
The first line has two integers m and n (2 ≤ m ≤ 100, 0 ≤ n ≤ 100), representing the number of vertices including two holes that give the initial string shape (m) and the number of pins (n). Each of the following l = m + n lines has two integers xi and yi (0 ≤ xi ≤ 1000, 0 ≤ yi ≤ 1000), representing a position Pi = (xi ,yi ) on the surface of the panel.
- Positions P1, ..., Pm give the initial shape of the string; i.e., the two holes are at P1 and Pm , and the string's shape is a polygonal chain whose vertices are Pi (i = 1, ..., m), in this order.
- Positions Pm+1, ..., Pm+n are the positions of the pins.
Note that no two points are at the same position. No three points are exactly on a straight line.
Output
For each dataset, the length of the part of the tightened string that remains on the surface of the panel should be output in a line. No extra characters should appear in the output.
No lengths in the output should have an error greater than 0.001.
Sample Input
6 16 5 4 11 988 474 975 459 16 985 12 984 982 242 227 140 266 45 410 92 570 237 644 370 567 406 424 336 290 756 220 634 251 511 404 575 554 726 643 868 571 907 403 845 283 10 4 261 196 943 289 859 925 56 822 112 383 514 0 1000 457 514 1000 0 485 233 224 710 242 850 654 485 915 140 663 26 5 0 953 180 0 299 501 37 301 325 124 162 507 84 140 913 409 635 157 645 555 894 229 598 223 783 514 765 137 599 445 695 126 859 462 599 312 838 167 708 563 565 258 945 283 251 454 125 111 28 469 1000 1000 185 319 717 296 9 315 372 249 203 528 15 15 200 247 859 597 340 134 967 247 421 623 1000 427 751 1000 102 737 448 0 978 510 556 907 0 582 627 201 697 963 616 608 345 819 810 809 437 706 702 695 448 474 605 474 329 355 691 350 816 231 313 216 864 360 772 278 756 747 529 639 513 525 0 0
Output for the Sample Input
2257.0518296609 3609.92159564177 2195.83727086364 3619.77160684813
