Chebyshev's Theorem
If n is a positive integer,
there exists at least one prime number greater than n and less than or equal to 2n.
This fact is known as Chebyshev's theorem or the Bertrand-Chebyshev theorem,
which had been conjectured by Joseph Louis François Bertrand (1822–1900)
and was proven by Pafnuty Lvovich Chebyshev (Пафнутий Львович Чебышёв, 1821–1894) in 1850.
Srinivasa Aiyangar Ramanujan (1887–1920) gave an elementary proof in his paper published in 1919.
Paul Erdős (1913–1996) discovered another elementary proof in 1932.
For example, there exist 4 prime numbers greater than 10 and less than or equal to 20, i.e. 11, 13, 17 and 19.
There exist 3 prime numbers greater than 14 and less than or equal to 28, i.e. 17, 19 and 23.
Your mission is to write a program that counts the prime numbers greater than n and less than or equal to 2n for each given positive integer n.
Using such a program, you can verify Chebyshev's theorem for individual positive integers.
Input
The input is a sequence of datasets.
A dataset is a line containing a single positive integer n.
You may assume n ≤ 123456.
The end of the input is indicated by a line containing a single zero.
It is not a dataset.
Output
The output should be composed of as many lines as the input datasets.
Each line should contain a single integer and should never contain extra characters.
The output integer corresponding to a dataset consisting of an integer n should be the number of the prime numbers p satisfying n < p ≤ 2n.
Sample Input
1
10
13
100
1000
10000
100000
0
Output for the Sample Input
The Balance of the World
The world should be finely balanced. Positive vs. negative,
light vs. shadow, and left vs. right brackets.
Your mission is to write a program that judges whether a string is balanced
with respect to brackets so that we can observe the balance of the
world.
A string that will be given to the program may have two kinds of brackets,
round (“( )”) and square (“[ ]”).
A string is balanced if and only if the following conditions hold.
- For every left round bracket (“(”), there is a corresponding
right round bracket (“)”) in the following part of the string.
- For every left square bracket (“[”), there is a corresponding
right square bracket (“]”) in the following part of the string.
- For every right bracket, there is a left bracket corresponding to it.
- Correspondences of brackets have to be one to one, that is, a
single bracket never corresponds to two or more brackets.
- For every pair of corresponding left and right brackets,
the substring between them is balanced.
Input
The input consists of one or more lines, each of which being a dataset.
A dataset is a string that consists of English alphabets,
space characters, and two kinds of brackets, round (“( )”) and square (“[ ]”),
terminated by a period. You can assume that every line has 100
characters or less.
The line formed by a single period indicates the end of the input,
which is not a dataset.
Output
For each dataset, output “yes” if the
string is balanced, or “no” otherwise, in a line.
There may not be any extra characters in the output.
Sample Input
So when I die (the [first] I will see in (heaven) is a score list).
[ first in ] ( first out ).
Half Moon tonight (At least it is better than no Moon at all].
A rope may form )( a trail in a maze.
Help( I[m being held prisoner in a fortune cookie factory)].
([ (([( [ ] ) ( ) (( ))] )) ]).
.
.
Output for the Sample Input
Identically Colored Panels Connection
Dr. Fukuoka has invented fancy panels.
Each panel has a square shape of a unit size and
has one of the six colors, namely, yellow, pink, red, purple, green and blue.
The panel has two remarkable properties.
One property is that, when two or more panels with the same color
are placed adjacently, their touching edges melt a little
and they are fused each other.
The fused panels are united into a polygonally shaped panel.
The other property is that the color of a panel can be changed
to one of six colors by giving an electrical shock.
The resulting color can be controlled by its waveform.
The electrical shock to an already united panel changes
the color of the whole to a specified single color.
Since he wants to investigate the strength with respect to the
color and the size of a united panel compared to unit panels,
he tries to unite panels into a polygonal panel with a specified color.

Figure C-1: panels and their initial colors
Since many panels are simultaneously synthesized and generated on a base plate
through some complex chemical processes,
the fabricated panels are randomly colored and
they are arranged in a rectangular shape on the base plate (Figure C-1).
Note that the two purple (color 4) panels in Figure C-1 are
already united at the initial state since they are
adjacent to each other.
Installing electrodes to a panel, and
changing its color several times by giving electrical shocks
according to an appropriate sequence for a specified target color,
he can make a united panel merge the adjacent panels
to unite them step by step
and can obtain a larger panel with the target color.
Unfortunately, panels will be broken when
they are struck by the sixth electrical shock.
That is, he can change the color of a panel or a united panel only
five times.
Let us consider a case
where the panel at the upper left corner of the panel configuration
(Figure C-1) is attached with the electrodes.
First, changing the color of the panel from yellow to blue,
the two adjacent panels are fused into a united panel (Figure C-2).

Figure C-2:
Change of the color of the panel at the upper left corner,
from yellow (color 1) to blue (color 6).
Second, changing the color of the upper left united panel from blue
to red, a united red panel that consists of three unit panels is newly formed
(Figure C-3).
Then, changing the color of the united panel from red to purple,
panels are united again to form a united panel of five unit panels
(Figure C-4).

Figure C-3:
Change of the color of the panel at the upper left corner,
from blue (color 6) to red (color 3).

Figure C-4:
Change of the color of the panel at the upper left corner,
from red (color 3) to purple (color 4).
Furthermore, through making a pink united panel in Figure C-5 by
changing the color from purple to pink,
then, the green united panel in Figure C-6 is obtained
by changing the color from pink to green.
The green united panel consists of ten unit panels.
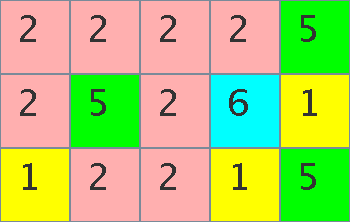
Figure C-5:
Change of the color of the panel at the upper left corner,
from purple (color 4) to pink (color 2).
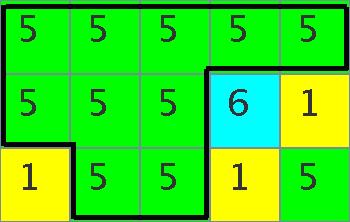
Figure C-6:
Change of the color of the panel at the upper left corner,
from pink (color 2) to green (color 5).
In order to check the strength of united panels with
various sizes and colors, he needs to unite as many panels
as possible with the target color.
Your job is to write a program that finds a sequence to change
the colors five times
in order to get the largest united panel with the target color.
Note that the electrodes are fixed to the panel at the upper left corner.
Input
The input consists of multiple datasets, each being in the following format.
h w c
p1,1 p1,2 ... p1,w
p2,1 p2,2 ... p2,w
...
ph,1 ph,2 ... ph,w
h and
w are positive integers no more than 8 that
represent the height and the width of the given rectangle.
c is a positive integer no more than 6 that represents
the target color of the finally united panel.
pi,j is a positive integer no more than 6
that represents the initial color of the panel at the position
(
i,
j).
The end of the input is indicated by a line that consists of
three zeros separated by single spaces.
Output
For each dataset, output the largest possible number of unit panels
in the united panel at the upper left corner with the target color
after five times of color changes of the panel
at the upper left corner.
No extra characters should occur in the output.
Sample Input
3 5 5
1 6 3 2 5
2 5 4 6 1
1 2 4 1 5
4 5 6
1 5 6 1 2
1 4 6 3 2
1 5 2 3 2
1 1 2 3 2
1 1 5
1
1 8 6
1 2 3 4 5 1 2 3
8 1 1
1
2
3
4
5
1
2
3
8 8 6
5 2 5 2 6 5 4 2
4 2 2 2 5 2 2 2
4 4 4 2 5 2 2 2
6 4 5 2 2 2 6 6
6 6 5 5 2 2 6 6
6 2 5 4 2 2 6 6
2 4 4 4 6 2 2 6
2 2 2 5 5 2 2 2
8 8 2
3 3 5 4 1 6 2 3
2 3 6 4 3 6 2 2
4 1 6 6 6 4 4 4
2 5 3 6 3 6 3 5
3 1 3 4 1 5 6 3
1 6 6 3 5 1 5 3
2 4 2 2 2 6 5 3
4 1 3 6 1 5 5 4
0 0 0
Output for the Sample Input
And Then, How Many Are There?
To Mr. Solitarius, who is a famous solo play game creator, a new idea
occurs like every day.
His new game requires discs of various colors and sizes.
To start with, all the discs are randomly scattered around the
center of a table.
During the play, you can remove a pair of discs of the same color if
neither of them has any discs on top of it.
Note that a disc is not considered to be on top of another when they
are externally tangent to each other.

Figure D-1: Seven discs on the table
For example, in Figure D-1, you can only remove the two black
discs first and then their removal makes it possible to remove the two
white ones.
In contrast, gray ones never become removable.
You are requested to write a computer program that, for given colors,
sizes, and initial placings of discs, calculates the maximum number of discs
that can be removed.
Input
The input consists of multiple datasets, each being in the
following format and representing the state of a game just after all
the discs are scattered.
n
x1 y1 r1 c1
x2 y2 r2 c2
...
xn yn rn cn
The first line consists of a positive integer n representing
the number of discs.
The following n lines, each containing 4 integers separated by
a single space, represent the colors, sizes, and initial placings of
the n discs in the following manner:
-
(xi, yi),
ri, and
ci are
the xy-coordinates of the center, the radius, and the color index
number, respectively, of the i-th disc, and
-
whenever the i-th disc is put on top of the j-th
disc, i < j must be satisfied.
You may assume that every color index number is between 1 and 4,
inclusive, and at most 6 discs in a dataset are of the same
color.
You may also assume that the x- and y-coordinates of the
center of every disc are between 0 and 100, inclusive, and the radius
between 1 and 100, inclusive.
The end of the input is indicated by a single zero.
Output
For each dataset, print a line containing an integer indicating the
maximum number of discs that can be removed.
Sample Input
4
0 0 50 1
0 0 50 2
100 0 50 1
0 0 100 2
7
12 40 8 1
10 40 10 2
30 40 10 2
10 10 10 1
20 10 9 3
30 10 8 3
40 10 7 3
2
0 0 100 1
100 32 5 1
0
Output for the Sample Input
Planning Rolling Blackouts
Faced with seriously tight power supply-demand balance, the
electric power company for which you are working implemented rolling
blackouts
in this spring. It divided the servicing area into several
groups of towns, and divided a day into several blackout periods. At
each blackout period of a day, one of the groups, which alternates
from one group to another, is cut off the electricity. By keeping the total demand of
electricity used by the rest of the towns within the supply
capacity, the company avoided unforeseeable large-scale blackout.
Working at the customer relations department, you had to listen to
so many complaints from the customers, which made you think that you
could have a better implementation. Most of the complaints are about the
frequent cut-offs. But you could have divided the area into a larger number of
groups, which resulted in less frequent cut-offs for each group. The
other complaints are about the complicated grouping (in fact, someone
said that the shapes of the groups are fractals), which makes it
impossible to understand which town belongs to which group without
closely inspecting into the grouping list publicized by the company.
With the rectangular servicing area and towns located in a grid form,
you could have made a simpler grouping.
When you talked your analysis directly to the president of the company, you are
appointed to plan rolling blackouts for this summer. Be careful what
you propose. Anyway, you need to divide the servicing area into
as many groups as possible with keeping total demand of electricity
within the supply capacity. It should also divide the towns into
simple and easy to remember groups.
Your task is to write a program, given a demand table (a table showing
electricity demand of each town) and the supply capacity, that answers
a grouping of towns that satisfy the following conditions.
- The grouping should be made by horizontally or vertically splitting
the area in a recursive manner. In other words, the grouping must
be a set of areas after applied the following splitting
procedure to a set containing only the entire area for zero or
more times:
(The splitting procedure) remove one area from the set,
either vertically or horizontally split it into two sub-areas,
and put the sub-areas into the set.
- The maximum suppressed demand of the grouping, which is the greatest total demand of the
all but one group, is no more than the supply capacity.
- The grouping has the largest number of groups among the groupings
that satisfy the above conditions 1 and 2.
- The grouping has the greatest amount of reserve power among the
groupings that satisfy the above conditions 1, 2 and 3, where the
reserve power of a grouping is the difference between the supply
capacity and the maximum suppressed demand.
Note that the condition 1 does not allow such a grouping shown in Figure E-1.
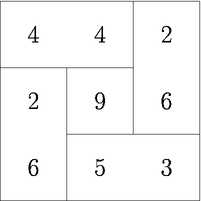
Figure E-1: A grouping that violates the condition 1
Input
The input consists of one or more datasets. Each dataset is given in
the following format.
h w s
u11 u12 ... u1w
u21 u22 ... u2w
...
uh1 uh2 ... uhw
The first line contains three positive integer numbers,
namely h, w and s, denoting the height and width
of the demand table and the power supply capacity. The following h
lines, each of which contains w integer numbers, denote demands of towns at respective
locations. Those figures are constrained as follows.
1 ≤ h, w ≤ 32
1 ≤ uij ≤ 100
Regrettably, you may assume that the supply capacity is less than the total demand of the area.
The last dataset is followed by a line containing three zeros.
Output
For each dataset, print a line having two integers indicating the
number of groups in the grouping that satisfies the conditions, and
the amount of the reserve power. Each line should not have any
character other than those numbers and a space in between.
Sample Input
3 3 33
4 4 2
2 9 6
6 5 3
3 4 15
1 2 1 2
2 1 2 1
1 2 1 2
32 32 1112
1 1 1 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 2
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1
2 1 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 2 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1
1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 2 1 1 1 2 1 1
1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1
1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1
1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1
1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1
2 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 2 2 1 1 2 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1
2 1 1 1 1 1 1 1 2 1 1 1 2 2 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 2 1 1 1 1 2 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 1 1 1 2 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 2 2
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1
1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1
1 1 1 2 1 1 2 1 1 1 2 1 2 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 2 2 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0
Output for the Sample Input
Watchdog Corporation
In Northern Kyushu, you are running a company
which rents watchdogs in response to the customers' order.
The distinguishing point of your service is that you also
install fences to enhance the performance of watchdogs.
The dog is put on a leash, which is tied up to a peg.
You are installing fences at the
border of the dog's reach, so that strangers approaching the
fence are taken care of by your dog.
There may be a rectangular building near the dog; the dog cannot
enter the building, but can go around it as long as the length of
the leash permits, as in Figure F-1. You do not need fences along the
building's wall.
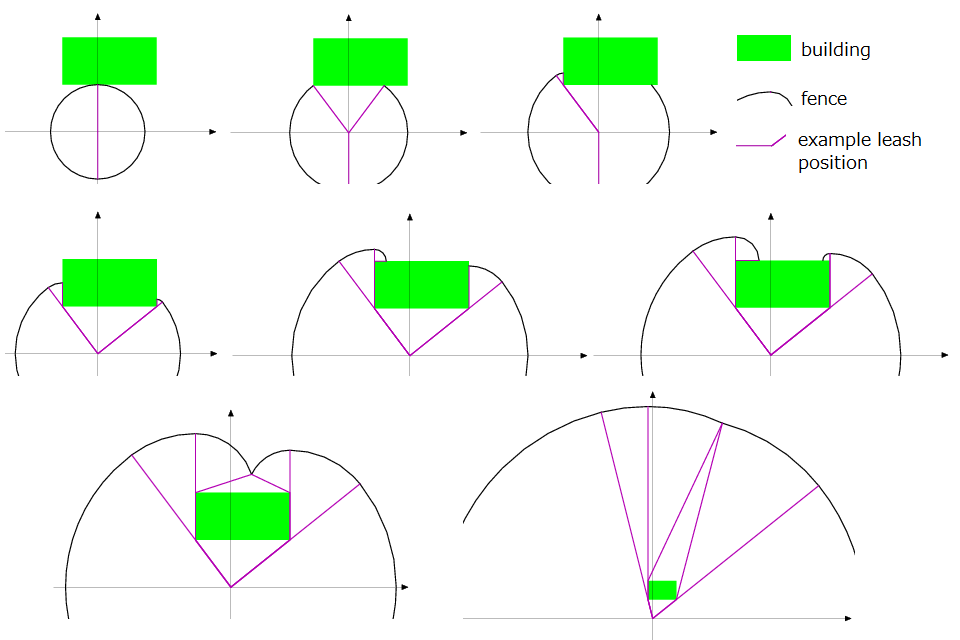
Figure F-1: Example fence layouts (some parts of the fences are omitted.)
Given the length of the leash and the position and the size of the
building, your program should calculate the length of the fence.
Input
The input consists of multiple datasets each consisting of
five integers in a line of the following format.
len x1 y1
x2 y2
len indicates the length of the leash.
x1, y1, x2
and y2 indicate the size and position of the
building in that a point with coordinate (x,y)
such that x1 < x <x2 and
y1 < y < y2 is
contained in the building. This means that
the building's walls are parallel to either the X-axis or Y-axis.
The peg is located on the origin.
You may assume that 0 < len ≤ 100, −100
≤ x1 < x2 ≤ 100 and
−100 ≤ y1 < y2 ≤ 100.
You may also assume that the peg is located apart from the
building (that is, neither inside nor on the border of the building).
The end of the input is indicated by a line containing five zeros.
Output
For each dataset, output the total length of the fences as a
single fractional number in
a line. There may not be any other characters in the output.
The output should not contain an error greater than 0.00001.
Sample Input
3 3 0 6 5
5 3 0 6 5
6 3 0 6 5
7 3 0 6 5
9 3 0 6 5
10 3 0 6 5
12 3 0 6 5
100 3 0 6 5
4 -3 4 5 8
5 -3 4 5 8
6 -3 4 5 8
64 -30 40 50 50
7 -3 4 5 8
10 -3 4 5 8
11 -3 4 5 8
14 -3 4 5 8
35 -3 4 5 8
100 -3 4 5 8
10 5 9 12 12
13 5 9 12 12
15 5 9 12 12
18 5 9 12 12
19 5 9 12 12
20 5 9 12 12
21 5 9 12 12
100 5 9 12 12
100 -5 1 -3 5
100 0 1 100 2
100 -1 99 100 100
10 -1 1 1 2
84 1 -77 5 -42
27 -12 -7 3 -4
0 0 0 0 0
Output for the Sample Input
18.84955592
26.77945045
31.69103413
39.54501577
55.51851918
63.83954229
75.38181750
628.05343108
25.13274123
24.98091545
29.43519428
318.90944272
35.02723766
55.44758990
64.23914179
89.33649537
219.11188064
627.48648370
62.83185307
76.33420961
88.61222855
112.17417345
121.59895141
126.16196589
132.25443447
628.23333565
628.18890261
626.17695473
613.16456638
62.61625003
527.84509612
168.07337509
A Broken Door
There is a rectangular maze consisting of a number of square rooms
arranged in grid. The maze is surrounded by
walls except for its entry and exit. The entry to the maze is at the
leftmost part of the upper side of the rectangular area, that is, the
upper side of the uppermost leftmost room of the maze is open. The
exit is located at the rightmost part of the lower side, likewise.
There is a wall between each pair of vertically or horizontally adjacent rooms. Such a wall has either
a door with a card key lock, or no door at all. If you insert a card
to a door, the door opens and you can pass the door. The opened door
will close immediately, and the inserted card won't return. You can
open any door with any card. You cannot go
through a wall that has no door.
When a maze map is given, you can easily determine how many cards are
needed to pass through the maze from the entry to the exit. In the
maze in Figure G-1, you can pass through it with ten cards,
following the path represented by the green arrows ( ) in Figure G-2.
) in Figure G-2.
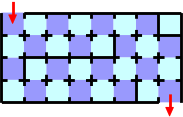
Figure G-1: A map of a maze
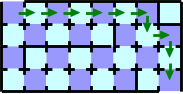
Figure G-2: One of the shortest paths
Now, you are informed that one of the doors is broken and can't be
passed. But you don't know which door is broken. If you insert a card
to a broken door, the inserted card immediately returns. However,
you can't tell a broken door from a working door just by its
appearance.
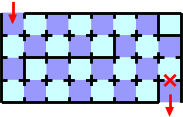
Figure G-3: A maze that potentially can't be passed through
If the door marked with a red X ( ) in Figure G-3 is broken, you have no way to pass through
the maze from the entry to the exit. However, you can pass the maze in
Figure G-1 whichever door is broken. When you intend to follow the
shortest path in Figure G-2, and find that the door marked with a red X in Figure G-4 is broken, you
might follow the path represented as green arrows. In this case, you
need twenty cards.
) in Figure G-3 is broken, you have no way to pass through
the maze from the entry to the exit. However, you can pass the maze in
Figure G-1 whichever door is broken. When you intend to follow the
shortest path in Figure G-2, and find that the door marked with a red X in Figure G-4 is broken, you
might follow the path represented as green arrows. In this case, you
need twenty cards.
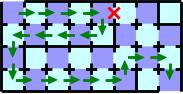
Figure G-4: A maze with a broken door
However, you can pass through the maze with less cards. You should
follow the path in Figure G-5, until you find the broken door.
The path is not the shortest path because it needs twelve
cards at least. After you've found a broken door on the path, you
should follow the shortest path to the exit that doesn't use the broken
door. With this strategy, you can pass the maze with sixteen cards
whichever door is broken. Figure G-6 shows one of the worst cases of
this strategy; it needs sixteen cards.
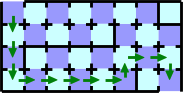
Figure G-5: The path before you find the broken door
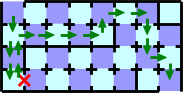
Figure G-6: One of the worst cases of the strategy
You are requested to write a program that prints the minimum number of
cards to pass the maze whichever door is broken.
Input
The input consists of one or more datasets, each of which represents a
maze. The number of datasets is no more than 100.
The first line of a dataset contains two integer numbers, the
height
h and the width
w of the rectangular maze, in
this order. You may assume that 2 ≤ h, w ≤ 30.
The following 2 ×
h − 1 lines of a dataset describe
whether there are doors between rooms or not. The first line starts
with a space and the rest of the line contains
w − 1
integers, 1 or 0, separated by a space. These indicate whether doors
connect horizontally adjoining rooms in the first row. An integer
0 indicates a door is placed, and 1 indicates no door is there. The
second line starts without a space and contains
w integers, 1 or 0,
separated by a space. These indicate whether doors connect
vertically adjoining rooms in the first and the second rows. An
integer 0/1 indicates a door is placed or not. The following lines
indicate placing of doors between horizontally and vertically
adjoining rooms, alternately, in the same manner.
The end of the input is indicated by a line containing two zeros.
Output
For each dataset, output a line having an integer indicating the
minimum number of cards needed.
If there exists no path to pass through the maze when a certain door is broken, output a line containing −1.
The line should not contain any character other than this number.
Sample Input
4 8
0 0 0 0 0 0 1
0 0 0 0 0 0 0 1
0 0 0 0 1 0 0
0 1 1 1 1 0 0 0
1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 1 0
4 8
0 0 0 0 0 0 1
0 0 0 0 0 0 0 1
0 0 0 0 1 0 0
0 1 1 1 1 0 0 0
1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 1
2 2
0
0 0
0
3 3
0 0
0 1 0
0 1
0 0 0
0 0
2 4
1 0 1
0 0 0 0
0 1 0
6 12
0 0 0 1 1 0 0 0 0 0 0
0 1 1 0 0 0 0 0 0 1 1 0
1 0 0 1 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 1 1 0 0 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 1 1 0 0 1 1 0 0
0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 1 1 0 0
0 0 0 0 0 1 1 0 0 1 0 0
1 0 0 0 0 0 0 1 0 0 0
20 20
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0
Output for the Sample Input







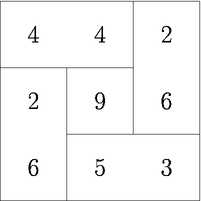

 ) in Figure G-2.
) in Figure G-2.



 ) in Figure G-3 is broken, you have no way to pass through
the maze from the entry to the exit. However, you can pass the maze in
Figure G-1 whichever door is broken. When you intend to follow the
shortest path in Figure G-2, and find that the door marked with a red X in Figure G-4 is broken, you
might follow the path represented as green arrows. In this case, you
need twenty cards.
) in Figure G-3 is broken, you have no way to pass through
the maze from the entry to the exit. However, you can pass the maze in
Figure G-1 whichever door is broken. When you intend to follow the
shortest path in Figure G-2, and find that the door marked with a red X in Figure G-4 is broken, you
might follow the path represented as green arrows. In this case, you
need twenty cards.


