Links
Problem A
Millennium
A wise king declared a new calendar. "Tomorrow shall be the first day of the calendar, that is, the day 1 of the month 1 of the year 1. Each year consists of 10 months, from month 1 through month 10, and starts from a big month. A common year shall start with a big month, followed by small months and big months one after another. Therefore the first month is a big month, the second month is a small month, the third a big month, ..., and the 10th and last month a small one. A big month consists of 20 days and a small month consists of 19 days. However years which are multiples of three, that are year 3, year 6, year 9, and so on, shall consist of 10 big months and no small month."
Many years have passed since the calendar started to be used. For celebration of the millennium day (the year 1000, month 1, day 1), a royal lottery is going to be organized to send gifts to those who have lived as many days as the number chosen by the lottery. Write a program that helps people calculate the number of days since their birthdate to the millennium day.
Input
The input is formatted as follows.
n
Y1 M1 D1
Y2 M2 D2
...
Yn Mn Dn
Here, the first line gives the number of datasets as a positive integer n, which is less than or equal to 100. It is followed by n datasets. Each dataset is formatted in a line and gives three positive integers, Yi (< 1000), Mi (≤ 10), and Di (≤ 20), that correspond to the year, month and day, respectively, of a person's birthdate in the king's calendar. These three numbers are separated by a space.
Output
For the birthdate specified in each dataset, print in a line the number of days from the birthdate, inclusive, to the millennium day, exclusive. Output lines should not contain any character other than this number.
Sample Input
8 1 1 1 344 3 1 696 5 1 182 9 5 998 8 7 344 2 19 696 4 19 999 10 20
Output for the Sample Input
196470 128976 59710 160715 252 128977 59712 1
Problem B
Recurring Decimals
A decimal representation of an integer can be transformed to another integer by rearranging the order of digits. Let us make a sequence using this fact.
A non-negative integer a0 and the number of digits L are given first. Applying the following rules, we obtain ai+1 from ai.
- Express the integer ai in decimal notation with L digits. Leading zeros are added if necessary. For example, the decimal notation with six digits of the number 2012 is 002012.
- Rearranging the digits, find the largest possible integer and the smallest possible integer; In the example above, the largest possible integer is 221000 and the smallest is 000122 = 122.
- A new integer ai+1 is obtained by subtracting the smallest possible integer from the largest. In the example above, we obtain 220878 subtracting 122 from 221000.
When you repeat this calculation, you will get a sequence of integers a0 , a1 , a2 , ... .
For example, starting with the integer 83268 and with the number of digits 6, you will get the following sequence of integers a0 , a1 , a2 , ... .
a0 = 083268
a1 = 886320 − 023688 = 862632
a2 = 866322 − 223668 = 642654
a3 = 665442 − 244566 = 420876
a4 = 876420 − 024678 = 851742
a5 = 875421 − 124578 = 750843
a6 = 875430 − 034578 = 840852
a7 = 885420 − 024588 = 860832
a8 = 886320 − 023688 = 862632
…
Because the number of digits to express integers is fixed, you will encounter occurrences of the same integer in the sequence a0 , a1 , a2 , ... eventually. Therefore you can always find a pair of i and j that satisfies the condition ai = aj (i > j ). In the example above, the pair (i = 8, j = 1) satisfies the condition because a8 = a1 = 862632.
Write a program that, given an initial integer a0 and a number of digits L, finds the smallest i that satisfies the condition ai = aj (i > j ).
Input
The input consists of multiple datasets. A dataset is a line containing two integers a0 and L separated by a space. a0 and L represent the initial integer of the sequence and the number of digits, respectively, where 1 ≤ L ≤ 6 and 0 ≤ a0 < 10L .
The end of the input is indicated by a line containing two zeros; it is not a dataset.
Output
For each dataset, find the smallest number i that satisfies the condition ai = aj (i > j ) and print a line containing three integers, j , ai and i − j. Numbers should be separated by a space. Leading zeros should be suppressed. Output lines should not contain extra characters.
You can assume that the above i is not greater than 20.
Sample Input
2012 4 83268 6 1112 4 0 1 99 2 0 0
Output for the Sample Input
3 6174 1 1 862632 7 5 6174 1 0 0 1 1 0 1
Problem C
Biased Dice
Professor Random, known for his research on randomized algorithms, is now conducting an experiment on biased dice. His experiment consists of dropping a number of dice onto a plane, one after another from a fixed position above the plane. The dice fall onto the plane or dice already there, without rotating, and may roll and fall according to their property. Then he observes and records the status of the stack formed on the plane, specifically, how many times each number appears on the faces visible from above. All the dice have the same size and their face numbering is identical, which we show in Figure C-1.
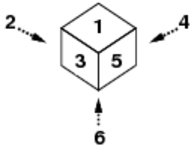
Figure C-1: Numbering of a die
The dice have very special properties, as in the following.
(1) Ordinary dice can roll in four directions, but the dice used in this experiment never roll in the directions of faces 1, 2 and 3; they can only roll in the directions of faces 4, 5 and 6. In the situation shown in Figure C-2, our die can only roll to one of two directions.
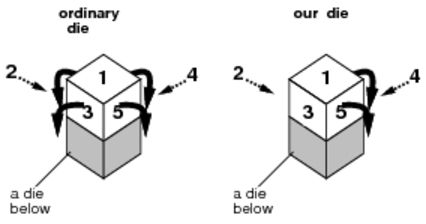
Figure C-2: An ordinary die and a biased die
(2) The die can only roll when it will fall down after rolling, as shown in Figure C-3. When multiple possibilities exist, the die rolls towards the face with the largest number among those directions it can roll to.
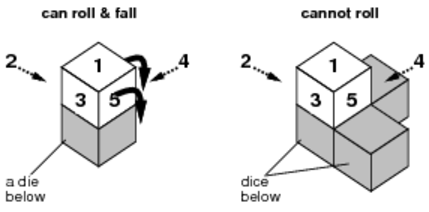
Figure C-3: A die can roll only when it can fall
(3) When a die rolls, it rolls exactly 90 degrees, and then falls straight down until its bottom face touches another die or the plane, as in the case [B] or [C] of Figure C-4.
(4) After rolling and falling, the die repeatedly does so according to the rules (1) to (3) above.
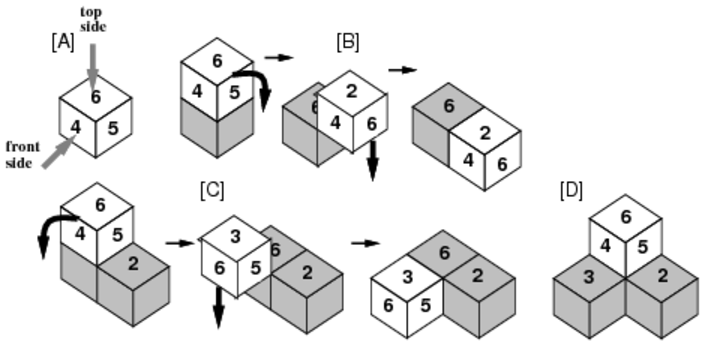
Figure C-4: Example stacking of biased dice
For example, when we drop four dice all in the same orientation, 6 at the top and 4 at the front, then a stack will be formed as shown in Figure C-4.
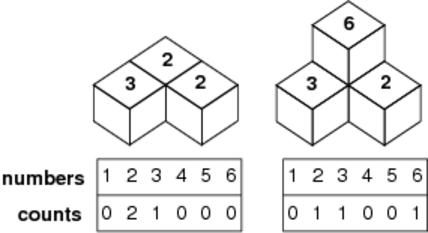
Figure C-5: Example records
After forming the stack, we count the numbers of faces with 1 through 6 visible from above and record them. For example, in the left case of Figure C-5, the record will be "0 2 1 0 0 0", and in the right case, "0 1 1 0 0 1".
Input
The input consists of several datasets each in the following format.
n
t1 f1
t2 f2
...
tn fn
Here, n (1 ≤ n ≤ 100) is an integer and is the number of the dice to be dropped. ti and fi (1 ≤ ti, fi ≤ 6) are two integers separated by a space and represent the numbers on the top and the front faces of the i-th die, when it is released, respectively.
The end of the input is indicated by a line containing a single zero.
Output
For each dataset, output six integers separated by a space. The integers represent the numbers of faces with 1 through 6 correspondingly, visible from above. There may not be any other characters in the output.
Sample Input
4 6 4 6 4 6 4 6 4 2 5 3 5 3 8 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 6 4 6 1 5 2 3 5 3 2 4 4 2 0
Output for the Sample Input
0 1 1 0 0 1 1 0 0 0 1 0 1 2 2 1 0 0 2 3 0 0 0 0
Problem D
Railway Connection
Tokyo has a very complex railway system. For example, there exists a partial map of lines and stations as shown in Figure D-1.
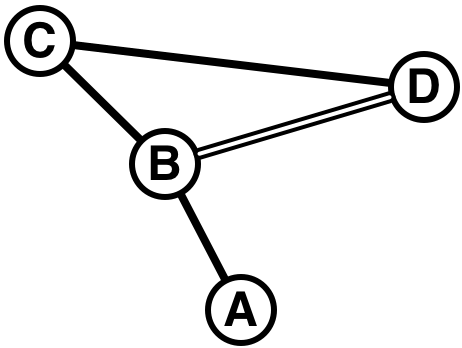
Figure D-1: A sample railway network
Suppose you are going to station D from station A. Obviously, the path with the shortest distance is A→B→D. However, the path with the shortest distance does not necessarily mean the minimum cost. Assume the lines A-B, B-C, and C-D are operated by one railway company, and the line B-D is operated by another company. In this case, the path A→B→C→D may cost less than A→B→D. One of the reasons is that the fare is not proportional to the distance. Usually, the longer the distance is, the fare per unit distance is lower. If one uses lines of more than one railway company, the fares charged by these companies are simply added together, and consequently the total cost may become higher although the distance is shorter than the path using lines of only one company.
In this problem, a railway network including multiple railway companies is given. The fare table (the rule to calculate the fare from the distance) of each company is also given. Your task is, given the starting point and the goal point, to write a program that computes the path with the least total fare.
Input
The input consists of multiple datasets, each in the following format.
n m c s g
x1 y1 d1 c1
...
xm ym dm cm
p1 ... pc
q1,1 ... q1,p1-1
r1,1 ... r1,p1
...
qc,1 ... qc,pc-1
rc,1 ... rc,pc
Every input item in a dataset is a non-negative integer. Input items in the same input line are separated by a space.
The first input line gives the size of the railway network and the intended trip. n is the number of stations (2 ≤ n ≤ 100). m is the number of lines connecting two stations (0 ≤ m ≤ 10000). c is the number of railway companies (1 ≤ c ≤ 20). s is the station index of the starting point (1 ≤ s ≤ n ). g is the station index of the goal point (1 ≤ g ≤ n, g ≠ s ).
The following m input lines give the details of (railway) lines. The i -th line connects two stations xi and yi (1 ≤ xi ≤ n, 1 ≤ yi ≤ n, xi ≠ yi ). Each line can be traveled in both directions. There may be two or more lines connecting the same pair of stations. di is the distance of the i -th line (1 ≤ di ≤ 200). ci is the company index of the railway company operating the line (1 ≤ ci ≤ c ).
The fare table (the relation between the distance and the fare) of each railway company can be expressed as a line chart. For the railway company j , the number of sections of the line chart is given by pj (1 ≤ pj ≤ 50). qj,k (1 ≤ k ≤ pj-1) gives the distance separating two sections of the chart (1 ≤ qj,k ≤ 10000). rj,k (1 ≤ k ≤ pj ) gives the fare increment per unit distance for the corresponding section of the chart (1 ≤ rj,k ≤ 100). More precisely, with the fare for the distance z denoted by fj (z ), the fare for distance z satisfying qj,k-1+1 ≤ z ≤ qj,k is computed by the recurrence relation fj (z) = fj (z-1)+rj,k. Assume that qj,0 and fj (0) are zero, and qj,pj is infinity.
For example, assume pj = 3, qj,1 = 3, qj,2 = 6, rj,1 = 10, rj,2 = 5, and rj,3 = 3. The fare table in this case is as follows.
| distance | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| fare | 10 | 20 | 30 | 35 | 40 | 45 | 48 | 51 | 54 |
qj,k increase monotonically with respect to k . rj,k decrease monotonically with respect to k .
The last dataset is followed by an input line containing five zeros (separated by a space).
Output
For each dataset in the input, the total fare for the best route (the route with the minimum total fare) should be output as a line. If the goal cannot be reached from the start, output "-1". An output line should not contain extra characters such as spaces.
Once a route from the start to the goal is determined, the total fare of the route is computed as follows. If two or more lines of the same railway company are used contiguously, the total distance of these lines is used to compute the fare of this section. The total fare of the route is the sum of fares of such "sections consisting of contiguous lines of the same company". Even if one uses two lines of the same company, if a line of another company is used between these two lines, the fares of sections including these two lines are computed independently. No company offers transit discount.
Sample Input
4 4 2 1 4 1 2 2 1 2 3 2 1 3 4 5 1 2 4 4 2 3 1 3 6 10 5 3 10 2 0 1 1 2 1 1 4 5 2 4 1 4 3 10 1 3 2 2 1 3 2 1 2 3 2 5 2 2 1 10 1 3 3 20 30 3 2 1 5 10 3 2 1 5 5 2 1 5 1 2 10 2 1 3 20 2 2 4 20 1 3 4 10 1 4 5 20 1 2 2 20 4 1 20 3 1 0 0 0 0 0
Output for the Sample Input
54 -1 63 130
Problem E
Chain-Confined Path
There is a chain consisting of multiple circles on a plane. The first (last) circle of the chain only intersects with the next (previous) circle, and each intermediate circle intersects only with the two neighboring circles.
Your task is to find the shortest path that satisfies the following conditions.
- The path connects the centers of the first circle and the last circle.
- The path is confined in the chain, that is, all the points on the path are located within or on at least one of the circles.
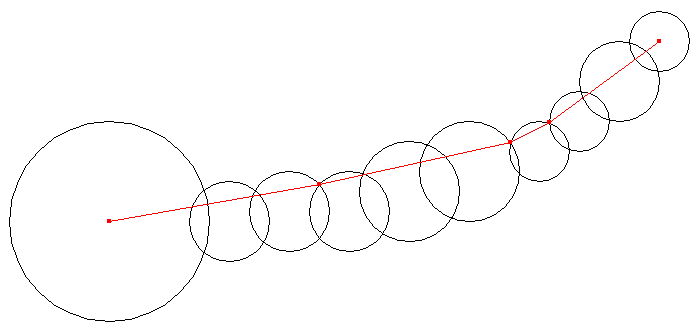
Figure E-1: An example chain and the corresponding shortest path
Input
The input consists of multiple datasets. Each dataset represents the shape of a chain in the following format.
n
x1 y1 r1
x2 y2 r2
...
xn yn rn
The first line of a dataset contains an integer n (3 ≤ n ≤ 100) representing the number of the circles. Each of the following n lines contains three integers separated by a single space. (xi, yi) and ri represent the center position and the radius of the i-th circle Ci. You can assume that 0 ≤ xi ≤ 1000, 0 ≤ yi ≤ 1000, and 1 ≤ ri ≤ 25.
You can assume that Ci and Ci+1 (1 ≤ i ≤ n−1) intersect at two separate points. When j ≥ i+2, Ci and Cj are apart and either of them does not contain the other. In addition, you can assume that any circle does not contain the center of any other circle.
The end of the input is indicated by a line containing a zero.
Figure E-1 corresponds to the first dataset of Sample Input below. Figure E-2 shows the shortest paths for the subsequent datasets of Sample Input.
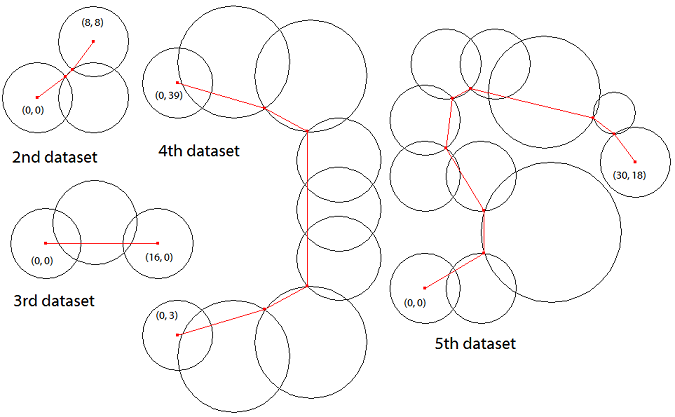
Figure E-2: Example chains and the corresponding shortest paths
Output
For each dataset, output a single line containing the length of the shortest chain-confined path between the centers of the first circle and the last circle. The value should not have an error greater than 0.001. No extra characters should appear in the output.
Sample Input
10 802 0 10 814 0 4 820 1 4 826 1 4 832 3 5 838 5 5 845 7 3 849 10 3 853 14 4 857 18 3 3 0 0 5 8 0 5 8 8 5 3 0 0 5 7 3 6 16 0 5 9 0 3 5 8 0 8 19 2 8 23 14 6 23 21 6 23 28 6 19 40 8 8 42 8 0 39 5 11 0 0 5 8 0 5 18 8 10 8 16 5 0 16 5 0 24 5 3 32 5 10 32 5 17 28 8 27 25 3 30 18 5 0
Output for the Sample Input
58.953437 11.414214 16.0 61.874812 63.195179
Problem F
Generic Poker
You have a deck of N × M cards. Each card in the deck has a rank. The range of ranks is 1 through M, and the deck includes N cards of each rank.
We denote a card with rank m by m here.
You can draw a hand of L cards at random from the deck. If the hand matches the given pattern, some bonus will be rewarded. A pattern is described as follows.
hand_pattern = card_pattern1 ' ' card_pattern2 ' ' ... ' ' card_patternL card_pattern = '*' | var_plus var_plus = variable | var_plus '+' variable = 'a' | 'b' | 'c'
- hand_pattern
- A hand matches the hand_pattern if each card_pattern in the hand_pattern matches with a distinct card in the hand.
- card_pattern
- If the card_pattern is an asterisk ('*'), it matches any card. Characters 'a', 'b', and 'c' denote variables and all the occurrences of the same variable match cards of the same rank. A card_pattern with a variable followed by plus ('+') characters matches a card whose rank is the sum of the rank corresponding to the variable and the number of plus characters. You can assume that, when a hand_pattern includes a card_pattern with a variable followed by some number of plus characters, it also includes card_patterns with that variable and all smaller numbers (including zero) of plus characters. For example, if 'a+++' appears in a hand_pattern, card_patterns 'a', 'a+', and 'a++' also appear in the hand_pattern.
There is no restriction on which ranks different variables mean. For example, 'a' and 'b' may or may not match cards of the same rank.
We show some example hand_patterns. The pattern
a * b a bmatches the hand:
3 3 10 10 9with 'a's and 'b's meaning 3 and 10 (or 10 and 3), respectively. This pattern also matches the following hand.
3 3 3 3 9In this case, both 'a's and 'b's mean 3. The pattern
a a+ a++ a+++ a++++matches the following hand.
4 5 6 7 8In this case, 'a' should mean 4.
Your mission is to write a program that computes the probability that a hand randomly drawn from the deck matches the given hand_pattern.
Input
The input is a sequence of datasets. Each dataset is formatted as follows.
N M L
card_pattern1 card_pattern2 ... card_patternL
The first line consists of three positive integers N, M, and L. N indicates the number of cards in each rank, M indicates the number of ranks, and L indicates the number of cards in a hand. N, M, and L are constrained as follows.
1 ≤ N ≤ 7
1 ≤ M ≤ 60
1 ≤ L ≤ 7
L ≤ N × M
The second line describes a hand_pattern.
The end of the input is indicated by a line containing three zeros separated by a single space.
Output
For each dataset, output a line containing a decimal fraction which means the probability of a hand matching the hand_pattern.
The output should not contain an error greater than 10−8.
No other characters should be contained in the output.
Sample Input
1 1 1 a 3 3 4 a+ * a * 2 2 3 a a b 2 2 3 * * * 2 2 3 * b b 2 2 2 a a 2 3 3 a a+ a++ 2 6 6 a a+ a++ b b+ b++ 4 13 5 a a * * * 4 13 5 a a b b * 4 13 5 a a a * * 4 13 5 a a+ a++ a+++ a++++ 4 13 5 * * * * * 4 13 5 a a a b b 4 13 5 a a a a * 7 60 7 a b a b c c * 7 60 7 * * * * * * * 7 60 7 a a+ a++ a+++ a++++ a+++++ a++++++ 1 14 4 b a+ a a 0 0 0
Output for the Sample Input
1.0000000000 0.8809523810 1.0000000000 1.0000000000 1.0000000000 0.3333333333 0.4000000000 0.1212121212 0.4929171669 0.0492196879 0.0228091236 0.0035460338 1.0000000000 0.0014405762 0.0002400960 0.0002967709 1.0000000000 0.0000001022 0.0000000000
Problem G
Patisserie ACM
Amber Claes Maes, a patissier, opened her own shop last month. She decided to submit her work to the International Chocolate Patissier Competition to promote her shop, and she was pursuing a recipe of sweet chocolate bars. After thousands of trials, she finally reached the recipe. However, the recipe required high skill levels to form chocolate to an orderly rectangular shape. Sadly, she has just made another strange-shaped chocolate bar as shown in Figure G-1.

Figure G-1: A strange-shaped chocolate bar
Each chocolate bar consists of many small rectangular segments of chocolate. Adjacent segments are separated with a groove in between them for ease of snapping. She planned to cut the strange-shaped chocolate bars into several rectangular pieces and sell them in her shop. She wants to cut each chocolate bar as follows.
- The bar must be cut along grooves.
- The bar must be cut into rectangular pieces.
- The bar must be cut into as few pieces as possible.

Figure G-2: An instance of cutting that follows the rules

Figure G-3: An instance of cutting that leaves a non-rectangular piece

Figure G-4: An instance of cutting that yields more pieces than Figure G-2
Your job is to write a program that computes the number of pieces of chocolate after cutting according to the rules.
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. Each dataset is formatted as follows.
h wThe integers h and w are the lengths of the two orthogonal dimensions of the chocolate, in number of segments. You may assume that 2 ≤ h ≤ 100 and 2 ≤ w ≤ 100. Each of the following h lines consists of w characters, each is either a "
r(1, 1) ... r(1, w)
r(2, 1) ... r(2, w)
...
r(h, 1) ... r(h, w)
- "
. ": There is no chocolate. - "
# ": There is a segment of chocolate.

Figure G-5: Disconnected chocolate bars

Figure G-6: A chocolate bar with a hole

Figure G-7: Another instance of a chocolate bar with a hole
Output
For each dataset, output a line containing the integer representing the number of chocolate pieces obtained by cutting according to the rules. No other characters are allowed in the output.
Sample Input
3 5 ###.# ##### ###.. 4 5 .#.## .#### ####. ##.#. 8 8 .#.#.#.# ######## .######. ######## .######. ######## .######. ######## 8 8 .#.#.#.# ######## .##.#.#. ##....## .##.###. ##...### .##.###. ###.#.## 4 4 #### #### #### #### 0 0
Output for the Sample Input
3 5 11 19 1
