Links
Problem A
ミレニアム
賢王が新しい暦を定めた.「明日を1年1月1日と定める.1年には1月から10月までの10ヶ月があり,大の月から始まる.ふつうの年は,1月が大の月,2月は小の月,3月は大の月,そして最後の10月は小の月というように,大の月と小の月が交互に訪れる.大の月の日数は20日,小の月の日数は19日である.しかし,3年,6年,9年,…のように,3で割り切れる年には,小の月は訪れず,10すべての月を大の月とする.」
幾年月が流れた.やがて1000年1月1日のミレニアム記念日の祝賀式において,誕生してからの日数が王立のくじ引きで選ばれた数と一致する国民に景品を与えることになった.国民らを手助けして,生まれた日からミレニアム記念日までの日数を計算するプログラムを奉ぜよ.
Input
入力全体は以下のような形式で表される.
n
Y1 M1 D1
Y2 M2 D2
...
Yn Mn Dn
ここで,最初の行にはデータセット数を表す100以下の正整数nが与えられる.この行に続いてn個のデータセットが与えられる.各データセットはそれぞれ1行であり,そのなかに三つの正整数Yi (< 1000),Mi (≤ 10),Di (≤ 20)を含む.これらの数は空白で区切られ,それぞれ,人物が生まれた日の王暦の年,月,日である.
Output
各データセットに与えられる誕生日について,その誕生日からミレニアム記念日までの日数をそれぞれ1行に出力しなさい.ただし,この日数に誕生日は勘定し,ミレニアム記念日は含まないものとする.出力行はこの数値以外の文字を含んではならない.
Sample Input
8 1 1 1 344 3 1 696 5 1 182 9 5 998 8 7 344 2 19 696 4 19 999 10 20
Output for the Sample Input
196470 128976 59710 160715 252 128977 59712 1
Problem B
繰り返す10進数
数の10進表現は数字を並べ替えることで別の数になる. このことを使って数列を作ってみよう.
最初に,非負の整数a0と桁数Lを与える. 以下の規則を適用してaiからai+1を得る.
- 整数aiを,L桁の10進数で表記する. 必要であれば上位の桁に 0 を付け加える. たとえば 2012 という数は 6 桁の10進数で表記する場合は 002012 となる.
- 各桁の数字を並べ替えて,最も大きい整数と最も小さい整数を作る. 上の例では,最も大きい整数は 221000 であり, 最も小さい整数は 000122 = 122となる.
- 最も大きい整数から最も小さな整数を引いて,整数ai+1を得る. 上の例では 221000 − 122 を計算して 220878 を得る.
この計算を繰り返すと,数列 a0 , a1 , a2 , ... が得られる.
例えば 83268 という整数と桁数6が与えられた時,この計算を繰り返すと次のような数列 a0 , a1 , a2 , ... が得られる.
a0 = 083268
a1 = 886320 − 023688 = 862632
a2 = 866322 − 223668 = 642654
a3 = 665442 − 244566 = 420876
a4 = 876420 − 024678 = 851742
a5 = 875421 − 124578 = 750843
a6 = 875430 − 034578 = 840852
a7 = 885420 − 024588 = 860832
a8 = 886320 − 023688 = 862632
…
整数を表すための桁数が指定されているので, a0 , a1 , a2 , ... と順に計算していくといずれ同じ数が現れる. すなわち,条件 ai = aj を満たすような i と j (ただし i > j ) の組が必ず存在する. 上の例では,a8 = a1 = 862632 なので (i = 8, j = 1) の組が条件を満たす.
最初の整数 a0 と桁数 L が与えられた場合に,条件 ai = aj (ただしi > j ) を満たす最小の i を求めるプログラムを作成せよ.
Input
入力は複数のデータセットからなる. 各データセットは2つの整数 a0 と L が1個のスペースで区切られた1行であり, a0 が最初の整数を, L が桁数を表す. ただし, 1 ≤ L ≤ 6 かつ 0 ≤ a0 < 10L である.
入力の終わりは2個の0を含む行で示される.この行はデータセットではない.
Output
各データセットに対して,条件 ai = aj (i > j ) を満たす最小の i を求め, そのときの j の値, ai の値, i − j の値をスペース1個ずつで区切り,1行で出力せよ. 数値を出力する時は,余分な上位のゼロは有ってはならない. 出力に余分な文字は含んではならない.
上記の i は20を超えないと仮定して構わない.
Sample Input
2012 4 83268 6 1112 4 0 1 99 2 0 0
Output for the Sample Input
3 6174 1 1 862632 7 5 6174 1 0 0 1 1 0 1
Problem C
偏りのあるサイコロ
確率的アルゴリズムの大家であるランダム教授は現在,偏りのあるサイコロの実験を行っている.実験というのは,平面の上方の決まった位置から次々にサイコ ロを落とすものである.サイコロは平面またはすでにそこにあるサイコロの上に回転せずに落ち,さらに転がり落ちることもある.結果としては,積み上がった 山の状態,具体的には上から見たときにどの目がいくつ見えるかを記録する.すべてのサイコロは同じ大きさで,数の振り方はすべて図C-1のようになってい る.
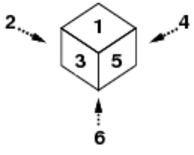
図C-1: サイコロの面の配置
ここで用いるサイコロは非常に特殊な性質を持っている.
(1)通常のサイコロは4方向に転がることができるが,ここで用いるサイコロは4,5,6の面の方向にしか転がらない(1,2,3の面の方向には転がれない).図C-2に示す状況では,ここで用いるサイコロ(our die)は2方向にしか転がらない.
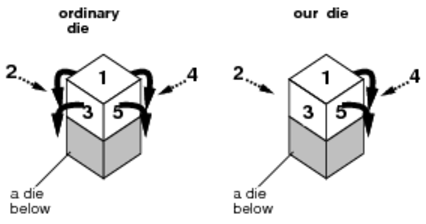
図C-2: 通常のサイコロと偏りのあるサイコロ
(2)サイコロが転がるのは,転がった後に落ちる時のみである.この様子を図C-3に示す.転がりうる方向が複数ある場合は,最も大きな目の面の方向に転がる.
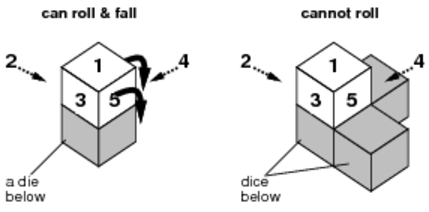
図C-3: サイコロは落ちられる時だけ転がれる
(3)転がる場合には,図C-4の[B],[C]のように,ちょうど90度回転した後,まっすぐ下に落ち,平面か他のサイコロの上に着地する.
(4)サイコロは一度転がり落ちた後も,(1)〜(3)の規則に従い繰り返し転がり落ちる.
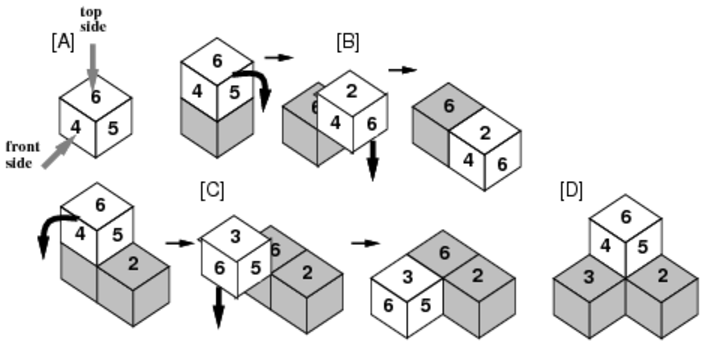
図C-4: 偏りのあるサイコロの積みあがり方の例
たとえば,同じ向き(上面が6,前面が4)で4つのサイコロを落下させた場合,図C-4のように山ができる.
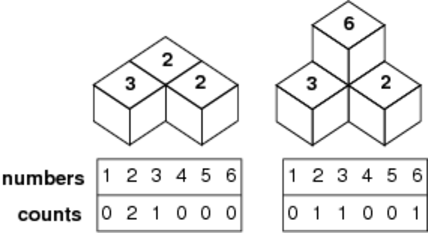
図C-5: 記録の例
山が完成したら,1から6までの面が上からいくつ見えるかを数えて記録する.たとえば図C-5の左の場合は記録は「0 2 1 0 0 0」となり,右の場合は「0 1 1 0 0 1」となる.
Input
入力は複数のデータセットからなり,各データセットは次の形式で表される.
n
t1 f1
t2 f2
...
tn fn
ここでn (1 ≤ n ≤ 100) は整数であり,落とすサイコロの個数である.ti とfi (1 ≤ ti, fi ≤ 6) は1つの空白で区切られた整数であり,i番目のサイコロから手を放す瞬間の上面と前面の目である.
入力の終わりは1つのゼロだけからなる行によって示される.
Output
各データセットごとに,6個の整数を1個の空白文字で区切って出力せよ.それぞれの整数は1〜6それぞれの目が上方向から何個見えるかを表す.出力にはこれら以外の文字があってはならない.
Sample Input
4 6 4 6 4 6 4 6 4 2 5 3 5 3 8 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 6 4 6 1 5 2 3 5 3 2 4 4 2 0
Output for the Sample Input
0 1 1 0 0 1 1 0 0 0 1 0 1 2 2 1 0 0 2 3 0 0 0 0
Problem D
鉄道乗り継ぎ
東京の鉄道ネットワークは非常に複雑である. たとえば,図D-1のような路線図が含まれている.
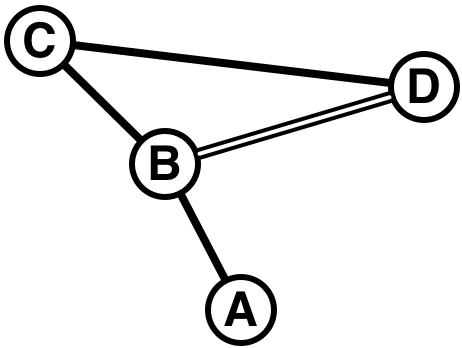
図D-1: 路線図の例
この路線図の上で,A駅からD駅に行きたいとする. 最短距離の経路を選ぶなら,A→B→Dと行けばよいことは明らかである. しかし,最短距離の経路が必ず最小コストの経路になるとは限らない. 図で,A-B,B-C,C-Dが同じ鉄道会社の線で,B-Dだけ別の会社の線だったとする. この場合,A→B→C→Dの経路の方がA→B→Dの経路より安いことがありうる. その要因の一つは,運賃が距離に比例していないことである. 距離が長いほど,単位距離当たりの運賃は安くなるように設定されていることが多い. 複数の会社の線を乗り継ぐと,それぞれの会社の運賃を単純に合計するので, 単一の会社の線だけを使った経路に比べて,距離は短くとも, 運賃は割高になってしまうことがあるのだ.
この問題では,複数の鉄道会社からなる路線図が与えられる. また,それぞれの会社の運賃表(距離から運賃を計算するルール)が与えられる. 出発地と目的地が与えられたとき,最も安い運賃の経路を求めるプログラムを書くことがあなたの仕事である.
Input
入力は複数のデータセットから構成される. 各データセットの形式は次に示すとおりである.
n m c s g
x1 y1 d1 c1
...
xm ym dm cm
p1 ... pc
q1,1 ... q1,p1-1
r1,1 ... r1,p1
...
qc,1 ... qc,pc-1
rc,1 ... rc,pc
データセットの中の入力項目は,すべて非負の整数である. 行中の入力項目の区切りは空白1個である.
最初の行は,鉄道ネットワークの大きさと実現したい旅行を規定する. n は駅の数である(2 ≤ n ≤ 100). m は駅と駅をつなぐ路線の数である(0 ≤ m ≤ 10000). c は鉄道会社の数である(1 ≤ c ≤ 20). s は出発地の駅番号である(1 ≤ s ≤ n). g は目的地の駅番号である(1 ≤ g ≤ n, g ≠ s).
続いて,m 本の路線のデータが順次与えられる. それぞれの行は,二つの駅xi とyi を結ぶ路線の記述である(1 ≤ xi ≤ n, 1 ≤ yi ≤ n, xi ≠ yi). 各路線は,どちらの方向の移動にも使える. 同じ二つの駅を結ぶ路線が2本以上存在することもあり得る. di は,その路線の長さ(移動距離)である(1 ≤ di ≤ 200). ci は,その路線を運営する鉄道会社の番号である(1 ≤ ci ≤ c).
各鉄道会社の運賃表(距離と運賃の関係)は折れ線グラフで与えられる. 鉄道会社j 番に対して, 折れ線の区間の数(折れ目の数プラス 1)がpj である (1 ≤ pj ≤ 50). qj,k (1 ≤ k ≤ pj-1)が折れ目の位置を示す距離の値である (1 ≤ qj,k ≤ 10000). rj,k (1 ≤ k ≤ pj)が該当する距離の範囲に対して距離 1 当たりの運賃の増分を与える (1 ≤ rj,k ≤ 100). より詳しく言えば,距離z のときの運賃を fj (z) と表すと, qj,k-1+1 ≤ z ≤ qj,k を満たす距離z に対して fj (z) = fj (z-1)+rj,k である. ただし,qj,0 とfj (0)はゼロ, qj,pj は無限大と仮定する.
たとえば,pj が 3 で, qj,1 = 3, qj,2 = 6, rj,1 = 10, rj,2 = 5, rj,3 = 3 だったとする. この場合の距離と運賃の対応関係は次のようになる.
| 距離 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 運賃 | 10 | 20 | 30 | 35 | 40 | 45 | 48 | 51 | 54 |
qj,k は,k に関して単調増加である. rj,k は,k に関して単調減少である.
最後のデータセットの直後に,空白で区切られた五つのゼロからなる行がある.
Output
入力の各データセットに対して,合計運賃が最小になるような経路を選んだときの所要運賃を答えなさい. ただし,出発地から目的地に到達できない場合は "-1" と出力すること. 出力行の中に,結果を表す文字以外のもの(たとえば空白)が含まれていてはならない.
出発地から目的地までの経路を定めたときの運賃の計算ルールは次のとおりとする. 同じ会社の複数の路線を連続して経由する場合は,これらの路線の合計距離に基づいて運賃を決める. 全体の運賃は,こうして決めた同一会社連続区間の運賃の総和である. 同じ会社の路線を複数利用していても,間にほかの会社の路線がはさまっている場合は,前後の区間の運賃を独立に計算する. 乗り継ぎ割引のような制度は存在しない.
Sample Input
4 4 2 1 4 1 2 2 1 2 3 2 1 3 4 5 1 2 4 4 2 3 1 3 6 10 5 3 10 2 0 1 1 2 1 1 4 5 2 4 1 4 3 10 1 3 2 2 1 3 2 1 2 3 2 5 2 2 1 10 1 3 3 20 30 3 2 1 5 10 3 2 1 5 5 2 1 5 1 2 10 2 1 3 20 2 2 4 20 1 3 4 10 1 4 5 20 1 2 2 20 4 1 20 3 1 0 0 0 0 0
Output for the Sample Input
54 -1 63 130
Problem E
鎖中経路
平面上の複数の円環から構成される鎖がある. 最初(最後)の円は,次(一つ前)の円だけと交差し, 中間の各円は隣の二つの円だけと交差する.
あなたの仕事は,以下の条件を満たす最短経路を見つけることである.
- 経路は,最初と最後の円の中心をつなぐ.
- 経路は鎖中にある.すなわち,経路上のすべての点は,少なくとも一つの円の内側もしくは円周上にある.
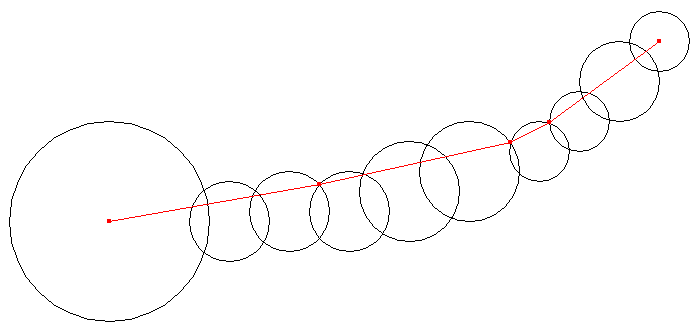
図 E-1: 鎖の例と対応する最短経路
Input
入力は複数のデータセットからなる. 各データセットは一つの鎖の形状を表し,その形式は以下のとおりである.
n
x1 y1 r1
x2 y2 r2
...
xn yn rn
データセットの最初の行は,円の個数を表す整数 n (3 ≤ n ≤ 100) のみからなる. 続く n 行のそれぞれは,空白文字 1 個で区切られた 3 個の整数からなる. (xi, yi) と ri は, i 番目の円 Ci の中心の位置と半径を表す. 0 ≤ xi ≤ 1000, 0 ≤ yi ≤ 1000, 1 ≤ ri ≤ 25 であると仮定してよい.
Ci と Ci+1 (1 ≤ i ≤ n−1) は,離れた 2 点で交差すると仮定してよい. j ≥ i+2 のとき,Ci と Cj は離れており,一方が他方を含むこともない. 加えて,それぞれの円は他の円の中心を内部に含むことがないと仮定してもよい.
入力の終わりは,ゼロを一つだけ含む行で表される.
なお,図 E-1 は,後に示す Sample Input 中の最初のデータセットに対応している. 図 E-2 は,Sample Input 中の引き続くデータセットに対する最短経路を示している.
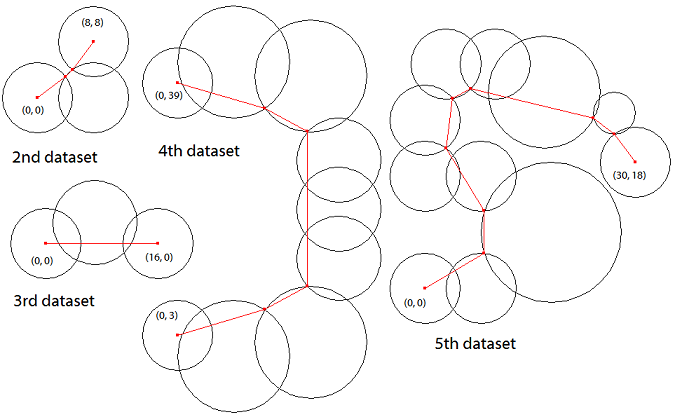
図 E-2: 鎖の例と対応する最短経路
Output
各データセットに対して,最初と最後の円の中心をつなぐ最短鎖中経路の長さを 1 行で出力せよ. 答えには 0.001 を超える誤差があってはいけない. それ以外の余計な文字を出力してはならない.
Sample Input
10 802 0 10 814 0 4 820 1 4 826 1 4 832 3 5 838 5 5 845 7 3 849 10 3 853 14 4 857 18 3 3 0 0 5 8 0 5 8 8 5 3 0 0 5 7 3 6 16 0 5 9 0 3 5 8 0 8 19 2 8 23 14 6 23 21 6 23 28 6 19 40 8 8 42 8 0 39 5 11 0 0 5 8 0 5 18 8 10 8 16 5 0 16 5 0 24 5 3 32 5 10 32 5 17 28 8 27 25 3 30 18 5 0
Output for the Sample Input
58.953437 11.414214 16.0 61.874812 63.195179
Problem F
一般化ポーカー
1からMのランクを持つN × M 枚のカードのデッキがある. それぞれのランクごとにN枚のカードが含まれている.
ランクmのカードのことを以下ではmと記述する.
デッキからL枚の手札をランダムに引くことができる.その手札 が与えられたパターンにマッチしているとボーナスが与えられる.パターンは, 以下のように記述される.
hand_pattern = card_pattern1 ' ' card_pattern2 ' ' ... ' ' card_patternL card_pattern = '*' | var_plus var_plus = variable | var_plus '+' variable = 'a' | 'b' | 'c'
- hand_pattern
- hand_pattern中の各card_patternがそれぞれ手札中の異なるカードにマッチすれば, その手札はhand_patternにマッチする.
- card_pattern
- card_patternがアステリスク('*')の時はどのカードにもマッチする. 文字'a', 'b', 'c'は変数を表し,同じ変数は同じランクのカードとマッチする. 変数の後に1個以上のプラス('+')を続けたパターンは,変数に対応するランクに'+'の個数を足して得られるラ ンクのカードにマッチする. 変数の後に'+'をいくつか続けたパターンがhand_patternに含まれる時は, 同じ変数の後に'+'をより少ない数(ゼロを含む)続けたパターンがすべてhand_patternに含まれると 仮定してよい.たとえば,'a+++'がhand_patternに現れる時は,'a', 'a+', 'a++' が hand_patternに現れる.
異なる変数の間には,表すランクについての制約はない. たとえば,'a'に対応するランクと'b'に対応するランクは同じでもよいし,異なっていてもよい.
hand_patternの例を示す.パターン
a * b a bは,'a'が3を, 'b'が10 を(または'a'が10を, 'b'が3を)表すとすると
3 3 10 10 9とマッチする. 同じパターンは手札
3 3 3 3 9ともマッチする.この時は,'a'も'b'も3を表す.パターン
a a+ a++ a+++ a++++は手札
4 5 6 7 8とマッチする.この場合,'a'は4になる.
デッキからランダムに取り出した手札が与えられたhand_patternにマッチする確率を求めるプログラムを作成しなさい.
Input
入力は複数のデータセットからなる.それぞれのデータセットは以下の形式からなる.
N M L
card_pattern1 card_pattern2 ... card_patternL
最初の行は空白で区切られた三つの正の整数N, M, Lを含んでいる.Nは同ランクのカードの数, Mはランクの数,Lは手札の枚数を示す.N, M, Lは以下の制約を満たす.
1 ≤ N ≤ 7
1 ≤ M ≤ 60
1 ≤ L ≤ 7
L ≤ N × M
2行目はhand_patternを記述している.
入力の終わりは空白一つで区切られたゼロ3個からなる行によって示される.
Output
各データセットについて,そのhand_patternに手札がマッチする確率を小数として出力せよ.
出力には10−8を超える誤差があってはならない.
それ以外の文字を含んでいてはならない.
Sample Input
1 1 1 a 3 3 4 a+ * a * 2 2 3 a a b 2 2 3 * * * 2 2 3 * b b 2 2 2 a a 2 3 3 a a+ a++ 2 6 6 a a+ a++ b b+ b++ 4 13 5 a a * * * 4 13 5 a a b b * 4 13 5 a a a * * 4 13 5 a a+ a++ a+++ a++++ 4 13 5 * * * * * 4 13 5 a a a b b 4 13 5 a a a a * 7 60 7 a b a b c c * 7 60 7 * * * * * * * 7 60 7 a a+ a++ a+++ a++++ a+++++ a++++++ 1 14 4 b a+ a a 0 0 0
Output for the Sample Input
1.0000000000 0.8809523810 1.0000000000 1.0000000000 1.0000000000 0.3333333333 0.4000000000 0.1212121212 0.4929171669 0.0492196879 0.0228091236 0.0035460338 1.0000000000 0.0014405762 0.0002400960 0.0002967709 1.0000000000 0.0000001022 0.0000000000
Problem G
ACM洋菓子店
先月自分の店をオープンしたお菓子職人のアンバー・C・マエスは,店の宣伝のために ICPC (International Chocolate Patissier Competition)に出品することにした. そのために,板チョコレートの試作を繰り返していたアンバーは, ついに本当においしいレシピを発見した.しかし,そのレシピではチョコレートをきれいな長方形に整形するために高度な技術が必要だった.つい今しがたも図G-1に示すような, おかしな形の板チョコレートを作ってしまったところだ.

図 G-1: おかしな形の板チョコレート
板チョコレートはたくさんの小長方形のチョコレートでできている.隣接する小長方形の間には溝が掘られており,割りやすくなっている. アンバーは,おかしな形の板チョコレートをいくつかの長方形の断片に切り分けて店で売ろうと考えた.彼女は次のように板チョコレートを切ることにした.
- 板チョコレートは溝に沿って切る.
- 断片が全て長方形になるように切り分ける.
- できるだけ少ない数の断片に切り分ける.

図 G-2: ルールに従って切り分けた例

図 G-3: 長方形でない断片を含むような切り分け方の例

図 G-4: 図G-2よりも多くの断片に切り分ける例
あなたの仕事は,このルールに従って板チョコレートを切り分けた時,いくつの断片に分かれるかを求めるプログラムを作ることである.
Input
入力は,複数のデータセットからなり,入力の終わりはスペースで区切られたゼロ2つからなる行である.各データセットは,次の形式をしている.
h wh と w は,板チョコレートの直交する2方向の長さを小長方形チョコレートの数で表した整数であり,2 ≤ h ≤ 100, 2 ≤ w ≤ 100 と仮定してよい.続く h 行はそれぞれ, w 個の文字で構成されており, 文字 r(i, j) は,場所 (i, j) の小長方形チョコレートの有無を表す.文字の意味は,次の通り.
r(1, 1) ... r(1, w)
r(2, 1) ... r(2, w)
...
r(h, 1) ... r(h, w)
- "
. ": 小長方形チョコレートなし - "
# ": 小長方形チョコレートあり

図 G-5: 連結していない板チョコレート

図 G-6: 穴のある形の板チョコレート

図 G-7: 穴のある形の板チョコレートのもう1つの例
Output
入力データセットごとに,ルールに従って切り分けた時の断片の数を表す整数のみからなる行を出力せよ.
Sample Input
3 5 ###.# ##### ###.. 4 5 .#.## .#### ####. ##.#. 8 8 .#.#.#.# ######## .######. ######## .######. ######## .######. ######## 8 8 .#.#.#.# ######## .##.#.#. ##....## .##.###. ##...### .##.###. ###.#.## 4 4 #### #### #### #### 0 0
Output for the Sample Input
3 5 11 19 1
