VAT (value-added tax) is a tax imposed at a certain rate proportional to the sale price.

Our store uses the following rules to calculate the after-tax prices.

• When the VAT rate is x%, for an item with the before-tax price of p yen, its after-tax price of the item is p (100+x) / 100 yen, fractions rounded off.
• The total after-tax price of multiple items paid at once is the sum of after-tax prices of the items.

The VAT rate is changed quite often. Our accountant has become aware that "different pairs of items that had the same total after-tax price may have different total after-tax prices after VAT rate changes." For example, when the VAT rate rises from 5% to 8%, a pair of items that had the total after-tax prices of 105 yen before can now have after-tax prices either of 107, 108, or 109 yen, as shown in the table below.

Before-tax prices of two items	After-tax price with 5% VAT	After-tax price with 8% VAT
20, 80	21 + 84 = 105	21 + 86 = 107
2, 99	2 + 103 = 105	2 + 106 = 108
13, 88	13 + 92 = 105	14 + 95 = 109

Our accountant is examining effects of VAT-rate changes on after-tax prices. You are asked to write a program that calculates the possible maximum total after-tax price of two items with the new VAT rate, knowing their total after-tax price before the VAT rate change.

The input consists of multiple datasets. Each dataset is in one line, which consists of three integers x, y, and s separated by a space. x is the VAT rate in percent before the VAT-rate change, y is the VAT rate in percent after the VAT-rate change, and s is the sum of after-tax prices of two items before the VAT-rate change. For these integers, 0 < x < 100, 0 < y < 100, 10 < s < 1000, and x ≠ y hold. For before-tax prices of items, all possibilities of 1 yen through s-1 yen should be considered.

The end of the input is specified by three zeros separated by a space.

For each dataset, output in a line the possible maximum total after-tax price when the VAT rate is changed to y%.

5 8 105
8 5 105
1 2 24
99 98 24
12 13 26
1 22 23
1 13 201
13 16 112
2 24 50
1 82 61
1 84 125
1 99 999
99 1 999
98 99 999
1 99 11
99 1 12
0 0 0

109
103
24
24
26
27
225
116
62
111
230
1972
508
1004
20
7

In the following table, an instance of a before-tax price pair that has the maximum after-tax price after the VAT-rate change is given for each dataset of the sample input.

Dataset	Before-tax prices	After-tax price with y% VAT
5 8 105	13, 88	14 + 95 = 109
8 5 105	12, 87	12 + 91 = 103
1 2 24	1, 23	1 + 23 = 24
99 98 24	1, 12	1 + 23 = 24
12 13 26	1, 23	1 + 25 = 26
1 22 23	1, 22	1 + 26 = 27
1 13 201	1,199	1 +224 = 225
13 16 112	25, 75	29 + 87 = 116
2 24 50	25, 25	31 + 31 = 62
1 82 61	11, 50	20 + 91 = 111
1 84 125	50, 75	92 +138 = 230
1 99 999	92,899	183+1789 =1972
99 1 999	1,502	1 +507 = 508
98 99 999	5,500	9 +995 =1004
1 99 11	1, 10	1 + 19 = 20
99 1 12	1, 6	1 + 6 = 7

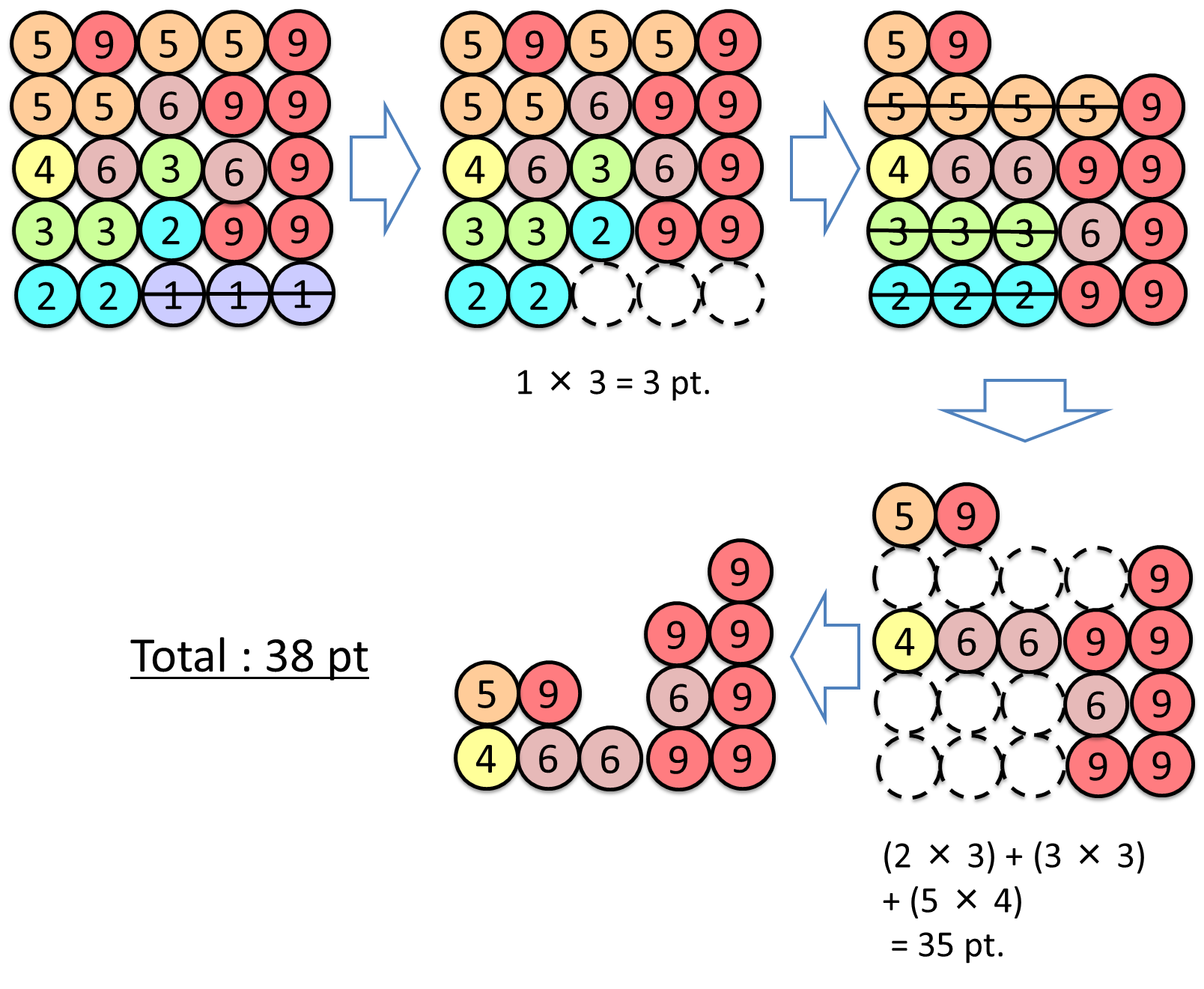
We are playing a puzzle. An upright board with H rows by 5 columns of cells, as shown in the figure below, is used in this puzzle. A stone engraved with a digit, one of 1 through 9, is placed in each of the cells. When three or more stones in horizontally adjacent cells are engraved with the same digit, the stones will disappear. If there are stones in the cells above the cell with a disappeared stone, the stones in the above cells will drop down, filling the vacancy.

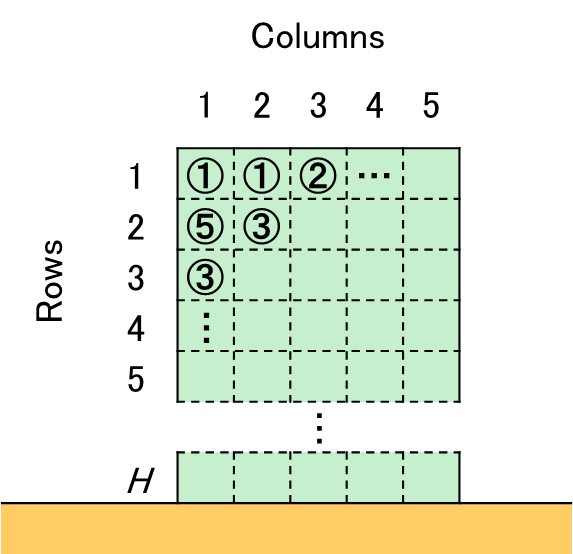
The puzzle proceeds taking the following steps.

1. When three or more stones in horizontally adjacent cells are engraved with the same digit, the stones will disappear. Disappearances of all such groups of stones take place simultaneously.
2. When stones are in the cells above the emptied cells, these stones drop down so that the emptied cells are filled.
3. After the completion of all stone drops, if one or more groups of stones satisfy the disappearance condition, repeat by returning to the step 1.

The score of this puzzle is the sum of the digits on the disappeared stones.

Write a program that calculates the score of given configurations of stones.

The input consists of multiple datasets. Each dataset is formed as follows.

Board height H
Stone placement of the row 1
Stone placement of the row 2
...
Stone placement of the row H

The first line specifies the height ( H ) of the puzzle board (1 ≤ H ≤ 10). The remaining H lines give placement of stones on each of the rows from top to bottom. The placements are given by five digits (1 through 9), separated by a space. These digits are engraved on the five stones in the corresponding row, in the same order.

The input ends with a line with a single zero.

For each dataset, output the score in a line. Output lines may not include any characters except the digits expressing the scores.

1
6 9 9 9 9
5
5 9 5 5 9
5 5 6 9 9
4 6 3 6 9
3 3 2 9 9
2 2 1 1 1
10
3 5 6 5 6
2 2 2 8 3
6 2 5 9 2
7 7 7 6 1
4 6 6 4 9
8 9 1 1 8
5 6 1 8 1
6 8 2 1 2
9 6 3 3 5
5 3 8 8 8
5
1 2 3 4 5
6 7 8 9 1
2 3 4 5 6
7 8 9 1 2
3 4 5 6 7
3
2 2 8 7 4
6 5 7 7 7
8 8 9 9 9
0

36
38
99
0
72

Mr. C is a vampire. If he is exposed to the sunlight directly, he turns into ash. Nevertheless, last night, he attended to the meeting of Immortal and Corpse Programmers Circle, and he has to go home in the near dawn. Fortunately, there are many tall buildings around Mr. C's home, and while the sunlight is blocked by the buildings, he can move around safely. The top end of the sun has just reached the horizon now. In how many seconds does Mr. C have to go into his safe coffin?

To simplify the problem, we represent the eastern dawn sky as a 2-dimensional x-y plane, where the x axis is horizontal and the y axis is vertical, and approximate building silhouettes by rectangles and the sun by a circle on this plane.

The x axis represents the horizon. We denote the time by t, and the current time is t=0. The radius of the sun is r and its center is at (0, -r) when the time t=0. The sun moves on the x-y plane in a uniform linear motion at a constant velocity of (0, 1) per second.

The sunlight is blocked if and only if the entire region of the sun (including its edge) is included in the union of the silhouettes (including their edges) and the region below the horizon (y ≤ 0).

Write a program that computes the time of the last moment when the sunlight is blocked.

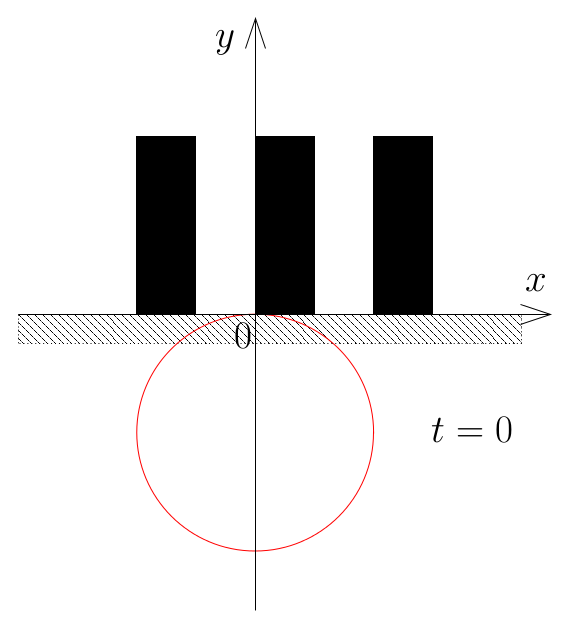
The following figure shows the layout of silhouettes and the position of the sun at the last moment when the sunlight is blocked, that corresponds to the first dataset of Sample Input below. As this figure indicates, there are possibilities that the last moment when the sunlight is blocked can be the time t=0.

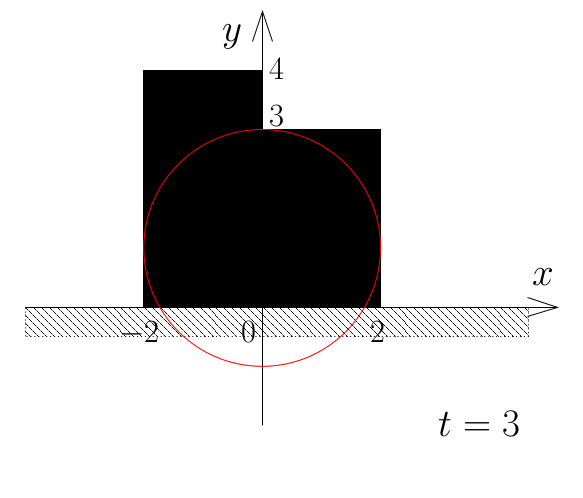
The sunlight is blocked even when two silhouettes share parts of their edges. The following figure shows the layout of silhouettes and the position of the sun at the last moment when the sunlight is blocked, corresponding to the second dataset of Sample Input. In this dataset the radius of the sun is 2 and there are two silhouettes: the one with height 4 is in -2 ≤ x ≤ 0, and the other with height 3 is in 0 ≤ x ≤ 2.

The input consists of multiple datasets. The first line of a dataset contains two integers r and n separated by a space. r is the radius of the sun and n is the number of silhouettes of the buildings. (1 ≤ r ≤ 20, 0 ≤ n ≤ 20)

Each of following n lines contains three integers x_li, x_ri, h_i (1 ≤ i ≤ n) separated by a space.

These three integers represent a silhouette rectangle of a building. The silhouette rectangle is parallel to the horizon, and its left and right edges are at x = x_li and x = x_ri, its top edge is at y = h_i, and its bottom edge is on the horizon. (-20 ≤ x_li < x_ri ≤ 20, 0 < h_i ≤ 20)

The end of the input is indicated by a line containing two zeros separated by a space.

Note that these silhouettes may overlap one another.

For each dataset, output a line containing the number indicating the time t of the last moment when the sunlight is blocked. The value should not have an error greater than 0.001. No extra characters should appear in the output.

2 3
-2 -1 3
0 1 3
2 3 3
2 2
-2 0 4
0 2 3
2 6
-3 3 1
-2 3 2
-1 3 3
0 3 4
1 3 5
2 3 6
2 6
-3 3 1
-3 2 2
-3 1 3
-3 0 4
-3 -1 5
-3 -2 6
0 0

0.0000
3.0000
2.2679
2.2679

A programmer developed a new encryption system. However, his system has an issue that two or more distinct strings are `encrypted' to the same string.

We have a string encrypted by his system. To decode the original string, we want to enumerate all the candidates of the string before the encryption. Your mission is to write a program for this task.

The encryption is performed taking the following steps. Given a string that consists only of lowercase letters ('a' to 'z').

1. Change the first 'b' to 'a'. If there is no 'b', do nothing.
2. Change the first 'c' to 'b'. If there is no 'c', do nothing.
...
25. Change the first 'z' to 'y'. If there is no 'z', do nothing.

The input consists of at most 100 datasets. Each dataset is a line containing an encrypted string. The encrypted string consists only of lowercase letters, and contains at least 1 and at most 20 characters.

The input ends with a line with a single '#' symbol.

For each dataset, the number of candidates n of the string before encryption should be printed in a line first, followed by lines each containing a candidate of the string before encryption. If n does not exceed 10, print all candidates in dictionary order; otherwise, print the first five and the last five candidates in dictionary order.

Here, dictionary order is recursively defined as follows. The empty string comes the first in dictionary order. For two nonempty strings x = x₁ ... x_k and y = y₁ ... y_l, the string x precedes the string y in dictionary order if

• x₁ precedes y₁ in alphabetical order ('a' to 'z'), or
• x₁ and y₁ are the same character and x₂ ... x_k precedes y₂ ... y_l in dictionary order.

enw
abc
abcdefghijklmnopqrst
z
#

1
fox
5
acc
acd
bbd
bcc
bcd
17711
acceeggiikkmmooqqssu
acceeggiikkmmooqqstt
acceeggiikkmmooqqstu
acceeggiikkmmooqrrtt
acceeggiikkmmooqrrtu
bcdefghijklmnopqrrtt
bcdefghijklmnopqrrtu
bcdefghijklmnopqrssu
bcdefghijklmnopqrstt
bcdefghijklmnopqrstu
0

ICPC islands once had been a popular tourist destination. For nature preservation, however, the government decided to prohibit entrance to the islands, and to remove all the man-made structures there. The hardest part of the project is to remove all the bridges connecting the islands.

There are n islands and n-1 bridges. The bridges are built so that all the islands are reachable from all the other islands by crossing one or more bridges. The bridge removal team can choose any island as the starting point, and can repeat either of the following steps.

• Move to another island by crossing a bridge that is connected to the current island.
• Remove one bridge that is connected to the current island, and stay at the same island after the removal.

Of course, a bridge, once removed, cannot be crossed in either direction. Crossing or removing a bridge both takes time proportional to the length of the bridge. Your task is to compute the shortest time necessary for removing all the bridges. Note that the island where the team starts can differ from where the team finishes the work.

The input consists of at most 100 datasets. Each dataset is formatted as follows.

n
p₂ p₃ ... p_n
d₂ d₃ ... d_n

The first integer n (3 ≤ n ≤ 800) is the number of the islands. The islands are numbered from 1 to n. The second line contains n-1 island numbers p_i (1 ≤ p_i < i), and tells that for each i from 2 to n the island i and the island p_i are connected by a bridge. The third line contains n-1 integers d_i (1 ≤ d_i ≤ 100,000) each denoting the length of the corresponding bridge. That is, the length of the bridge connecting the island i and p_i is d_i. It takes d_i units of time to cross the bridge, and also the same units of time to remove it. Note that, with this input format, it is assured that all the islands are reachable each other by crossing one or more bridges.

The input ends with a line with a single zero.

For each dataset, print the minimum time units required to remove all the bridges in a single line. Each line should not have any character other than this number.

4
1 2 3
10 20 30
10
1 2 2 1 5 5 1 8 8
10 1 1 20 1 1 30 1 1
3
1 1
1 1
0

80
136
2

The work of die makers starts early in the morning.

You are a die maker. You receive orders from customers, and make various kinds of dice every day. Today, you received an order of a cubic die with six numbers t₁, t₂, ..., t₆ on whichever faces.

For making the ordered die, you use a tool of flat-board shape. You initially have a die with a zero on each face. If you rotate the die by 90 degrees on the tool towards one of northward, southward, eastward, and southward, the number on the face that newly touches the tool is increased by one. By rotating the die towards appropriate directions repeatedly, you may obtain the ordered die.

The final numbers on the faces of the die is determined by the sequence of directions towards which you rotate the die. We call the string that represents the sequence of directions an operation sequence. Formally, we define operation sequences as follows. An operation sequence consists of n characters, where n is the number of rotations made. If you rotate the die eastward in the i-th rotation, the i-th character of the operation sequence is E. Similarly, if you rotate it westward, it is W, if southward, it is S, otherwise, if northward, it is N. For example, the operation sequence NWS represents the sequence of three rotations, northward first, westward next, and finally southward.

Given six integers of the customer's order, compute an operation sequence that makes a die to order. If there are two or more possibilities, you should compute the earliest operation sequence in dictionary order.

The input consists of multiple datasets. The number of datasets does not exceed 40. Each dataset has the following form.

t₁ t₂ t₃ t₄ t₅ t₆
p q

t₁, t₂, ..., t₆ are integers that represent the order from the customer. Further, p and q are positive integers that specify the output range of the operation sequence (see the details below).

Each dataset satisfies 0 ≤ t₁ ≤ t₂ ≤ ... ≤ t₆ ≤ 5,000 and 1 ≤ p ≤ q ≤ t₁+t₂+...+t₆. A line containing six zeros denotes the end of the input.

For each dataset, print the subsequence, from the p-th position to the q-th position, inclusively, of the operation sequence that is the earliest in dictionary order. If it is impossible to make the ordered die, print impossible.

Here, dictionary order is recursively defined as follows. The empty string comes the first in dictionary order. For two nonempty strings x = x₁ ... x_k and y = y₁ ... y_l, the string x precedes the string y in dictionary order if

• x₁ precedes y₁ in alphabetical order ('A' to 'Z'), or
• x₁ and y₁ are the same character and x₂ ... x_k precedes y₂ ... y_l in dictionary order.

1 1 1 1 1 1
1 6
1 1 1 1 1 1
4 5
0 0 0 0 0 2
1 2
0 0 2 2 2 4
5 9
1 2 3 4 5 6
15 16
0 1 2 3 5 9
13 16
2 13 22 27 31 91
100 170
0 0 0 0 0 0

EEENEE
NE
impossible
NSSNW
EN
EWNS
SNSNSNSNSNSNSNSNSNSNSNSSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNSNWEWE

There are one or more circles on a plane. Any two circles have different center positions and/or different radiuses. A circle may intersect with another circle, but no three or more circles have areas nor points shared by all of them. A circle may completely contain another circle or two circles may intersect at two separate points, but you can assume that the circumferences of two circles never touch at a single point.

Your task is to judge whether there exists a path that connects the given two points, P and Q, without crossing the circumferences of the circles. You are given one or more point pairs for each layout of circles.

In the case of Figure G-1, we can connect P and Q₁ without crossing the circumferences of the circles, but we cannot connect P with Q₂, Q₃, or Q₄ without crossing the circumferences of the circles.

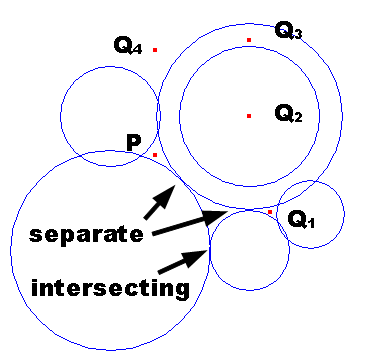
Figure G-1: Sample layout of circles and points

The input consists of multiple datasets, each in the following format.

n m
Cx₁ Cy₁ r₁
...
Cx_n Cy_n r_n
Px₁ Py₁ Qx₁ Qy₁
...
Px_m Py_m Qx_m Qy_m

The first line of a dataset contains two integers n and m separated by a space. n represents the number of circles, and you can assume 1 ≤ n ≤ 100. m represents the number of point pairs, and you can assume 1 ≤ m ≤ 10. Each of the following n lines contains three integers separated by a single space. (Cx_i, Cy_i) and r_i represent the center position and the radius of the i-th circle, respectively. Each of the following m lines contains four integers separated by a single space. These four integers represent coordinates of two separate points P_j = (Px_j, Py_j) and Q_j =(Qx_j, Qy_j). These two points P_j and Q_j form the j-th point pair. You can assume 0 ≤ Cx_i ≤ 10000, 0 ≤ Cy_i ≤ 10000, 1 ≤ r_i ≤ 1000, 0 ≤ Px_j ≤ 10000, 0 ≤ Py_j ≤ 10000, 0 ≤ Qx_j ≤ 10000, 0 ≤ Qy_j ≤ 10000. In addition, you can assume P_j or Q_j are not located on the circumference of any circle.

The end of the input is indicated by a line containing two zeros separated by a space.

Figure G-1 shows the layout of the circles and the points in the first dataset of the sample input below. Figure G-2 shows the layouts of the subsequent datasets in the sample input.

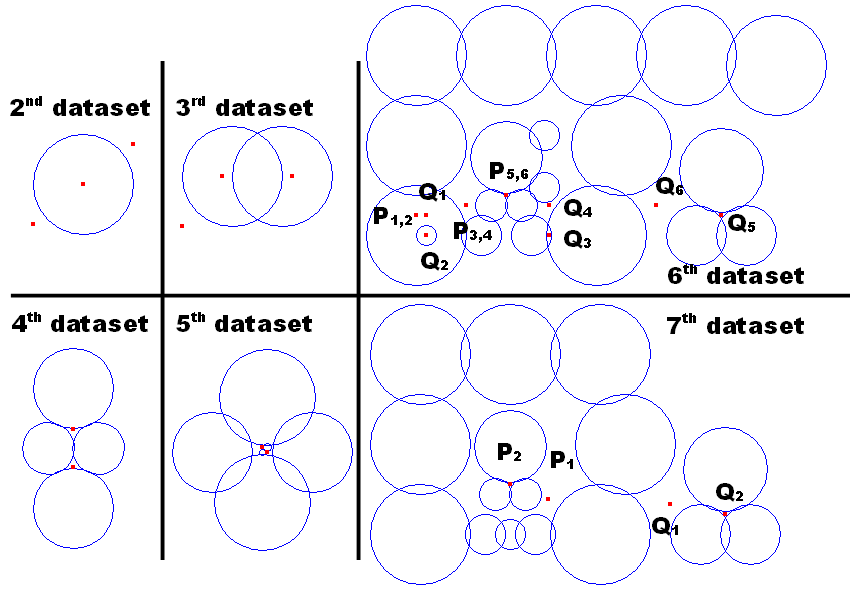
Figure G-2: Sample layout of circles and points

For each dataset, output a single line containing the m results separated by a space. The j-th result should be "YES" if there exists a path connecting P_j and Q_j, and "NO" otherwise.

5 3
0 0 1000
1399 1331 931
0 1331 500
1398 0 400
2000 360 340
450 950 1600 380
450 950 1399 1331
450 950 450 2000
1 2
50 50 50
0 10 100 90
0 10 50 50
2 2
50 50 50
100 50 50
40 50 110 50
40 50 0 0
4 1
25 100 26
75 100 26
50 40 40
50 160 40
50 81 50 119
6 1
100 50 40
0 50 40
50 0 48
50 50 3
55 55 4
55 105 48
50 55 55 50
20 6
270 180 50
360 170 50
0 0 50
10 0 10
0 90 50
0 180 50
90 180 50
180 180 50
205 90 50
180 0 50
65 0 20
75 30 16
90 78 36
105 30 16
115 0 20
128 48 15
128 100 15
280 0 30
330 0 30
305 65 42
0 20 10 20
0 20 10 0
50 30 133 0
50 30 133 30
90 40 305 20
90 40 240 30
16 2
0 0 50
0 90 50
0 180 50
90 180 50
180 180 50
205 90 50
180 0 50
65 0 20
115 0 20
90 0 15
280 0 30
330 0 30
305 65 42
75 40 16
90 88 36
105 40 16
128 35 250 30
90 50 305 20
0 0

YES NO NO
YES NO
NO NO
NO
YES
YES NO NO YES NO NO
NO NO