国際競技プログラミング大学 (International Competitive Programming College) は，競技プログラミングの研究でよく知られた大学である． この大学の志願者は入学試験を受験しなくてはいけない．

入学試験の合格者は以下のように選ぶ．

• どの合格者の得点も，どの不合格者の得点より高い．
• 合格者数 n は n_min 人以上，n_max 人以下とする． n はこの範囲内でギャップを最大とするものでなくてはいけない． ギャップとは合格者の最低点と不合格者の最高点の差である．
• 同じギャップになる n が複数あるときは，その中で n が最大になるように選ぶ．

Sample Input の最初のふたつの例を見てみよう． 最初の例では，n_min が 2, n_max が 4 で，5 人の受験者の得点が 100, 90, 82, 70, 65 となっている． 合格者を 2, 3, 4 人としたときのギャップは，それぞれ 8, 12, 5 となる． n としてはギャップが最大となる 3 を選ばなくてはいけない．

2 番目の例では，n_min が 2, n_max が 4 で，5 人の受験者の得点が 100, 90, 80, 75, 65 となっている． 合格者を 2, 3, 4 人としたときのギャップは，それぞれ 10, 5, 10 となる． ギャップは合格者 2 人および 4 人のときに最大となるが，n としてはそのうちの最大の 4 を選ばなくてはいけない．

あなたには，この規則に基づいて合格者数を計算するプログラムを作ってほしい．

入力は複数のデータセットからなる．各データセットは以下の形式で与えられる．

m n_min n_max
P₁
P₂
...
P_m

各データセットの最初の行は空白ひとつで区切られたみっつの整数からなる． m は受験者の人数，n_min は合格者の最小人数，n_max は合格者の最大人数を表す． その後に続く m 行は，整数 P_i を含むが，これらは各受験者の得点を表す． 得点は高い順に並べられている． これらの数は 0 < n_min < n_max < m ≤ 200, 0 ≤ P_i ≤ 10000 (1 ≤ i ≤ m), P_nmin > P_nmax+1 を満たす． これにより，条件を満たす n が存在することが保証される．

入力の終わりは，空白で区切られたみっつのゼロからなる行によって示される．

各データセットについて，合格者の人数を1行で出力しなさい．

5 2 4
100
90
82
70
65
5 2 4
100
90
80
75
65
3 1 2
5000
4000
3000
4 2 3
10000
10000
8000
8000
4 2 3
10000
10000
10000
8000
5 2 3
100
80
68
60
45
0 0 0

3
4
2
2
3
2

短句とは，日本の短歌と俳句に触発されて創作された定型詩である． 短句は 'a' から 'z' までの小文字の単語の並びであり，次の条件を満たさなければならない．

（短句の条件）
単語の並びを五つにうまく区切ることで，最初の区切中の単語の総文字数が 5，次が 7，以下，5，7，7 と続くようにできる．

次のものは短句の一例である．

do the best
and enjoy today
at acm icpc

この例では，9 単語の並びを (1) "do" と "the"，(2) "best" と "and"，(3) "enjoy"，(4) "today" と "at"，(5) "acm" と "icpc" の五つに区切ると，それぞれ総文字数 5，7，5，7，7 となる．これは確かに短句の条件を満たしている．

さて，あなたの会社が出版する雑誌「短句詩壇」にはたくさんの投稿が寄せられている． しかし，不幸な事故により，投稿された短句の先頭や末尾に見当違いな語句が追加されてしまったようである． 先頭や末尾に見当違いな語句を含み得る単語の並びから，元の短句を見つけ出すプログラムを作成して欲しい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
w₁
...
w_n

n は単語数を表す． n は 40 を超えない正の整数である． w_i は i 番目の単語であり，'a' から 'z' までの英小文字のみからなる． 各単語の長さは 1 以上 10 以下である． どのデータセットも必ず短句を含んでいると仮定して良い．

入力の終わりはゼロだけからなる行で表される．

各データセットについて，短句の先頭の単語が w_i となるような i のみからなる行を出力せよ． 複数の短句がデータセット中に出現する場合には，最初のものを出力すること．

9
do
the
best
and
enjoy
today
at
acm
icpc
14
oh
yes
by
far
it
is
wow
so
bad
to
me
you
know
hey
15
abcde
fghijkl
mnopq
rstuvwx
yzz
abcde
fghijkl
mnopq
rstuvwx
yz
abcde
fghijkl
mnopq
rstuvwx
yz
0

1
2
6

数学では，一般的に括弧を使って計算の順序を表現する． たとえば，7 × (3 + 2) は 3 + 2 を先に計算して， その結果を 7 に掛ける式であって，7 × 3 の結果に 2 を足す式ではない． しかし，世の中には括弧の存在を快く思わない人たちがいる． 国際反括弧会議 (International Counter of Parentheses Council) では，括弧を使わない記法を世界標準にしようとしている． 彼等は日夜括弧を使わない記法を研究している．

国際反括弧会議のメンバーである都九波博士は，括弧を使わない新しい記法を考案した． 博士が考案した記法では，加算演算子 (+)，乗算演算子 (*)，あるいは整数からなる行を並べて式を表す． 式は，整数ひとつか，被演算子への演算子の適用のどちらかである． 整数は十進数で 1 行に表記される． 演算子の適用の場合は，演算子の行を先に書き，直後の行から演算子が適用されるふたつ以上の被演算子を並べて書くことで表現する．被演算子は再帰的に同じ記法で表記した式である． 被演算子が演算子の適用である場合，被演算子が複数の行にわたることになる．

式はいくらでも入れ子になるので，どの演算子がどの被演算子に適用されるのかをわかるようにしなければならない． そのために，式には入れ子レベルを考える． 最上位の式は入れ子レベル 0 である． レベル n の式が演算子適用の場合，その被演算子はレベル n + 1 の式になる． 式の最初の行は入れ子レベルの数だけのピリオド (.) から始める．

例えば，通常の数学で 2 + 3 と書く式は図1 のように書く． 演算子はふたつ以上の被演算子に適用でき，+ と * はそれぞれ全ての被演算子の総和や，全ての被演算子を掛け合わせる演算を表す． 例えば，図2 は 2 と 3 と 4 を掛け合わせる式である． 複雑な例では，通常の数学での (2 + 3 + 4) × 5 は図3 のように書け， (2 + 3) × 4 × 5 は図4 のように書ける．

+
.2
.3

図1: 2 + 3

*
.2
.3
.4

図2: 2, 3, 4 を全て掛ける式

*
.+
..2
..3
..4
.5

図3: (2 + 3 + 4) × 5

*
.+
..2
..3
.4
.5

図4: (2 + 3) × 4 × 5

あなたの仕事は，博士を手伝ってこの記法で書かれた式の値を計算するプログラムを作ることだ．

入力は複数のデータセットからなる． データセットの 1 行目は 1 以上の整数 n だけを含む行である． 引き続く n 行には都九波博士の考案した記法でひとつの式が書かれている．

式に含まれる整数は全て 1 桁であり，ひとつの式に含まれる整数は 9 個以下であると仮定してよい． また，入力される式は全て正確に博士の記法に従っていると仮定してよい． 入力に空白などの余分な文字や空行は含まれていない．

最後のデータセットの直後には，ひとつのゼロだけからなる行がある．

各データセットについて，式の値のみからなる行を出力せよ．

1
9
4
+
.1
.2
.3
9
+
.0
.+
..*
...1
...*
....1
....2
..0
10
+
.+
..6
..2
.+
..1
..*
...7
...6
.3
0

9
6
2
54

日本の有名な貯金手法のひとつとして 500 円玉貯金が知られている．方法は簡単で，買い物のお釣りに 500 円玉があったらそれを貯金箱に入れるだけだ．通常，10 年もすれば貯金箱に 100 万円貯まっているだろう．

世の中には 500 円玉貯金に積極的な人々がいる．彼らは，買い物の際に 1000 円札と小銭をうまく出すことによって 500 円玉を効率よく得られるように努力している．例えば，817 円の支払いに 1320 円（1000 円札 1 枚，100 円玉 3 枚，10 円玉 2 枚）を出すことで，お釣りとして 500 円玉 1 枚（と 1 円玉 3 枚）が手に入る．

君の友達も 500 円玉貯金にとり憑かれたひとりだ．彼は観光のための旅に出かけようとしており，その道中にいくつかの土産物屋を順に訪れることを計画している．これらの土産物屋には各店に土産物が 1 種類ずつあり，彼はそれらの値段のリストを持っている．彼は，これらの土産物をうまく買い，500 円玉を 1 枚でも多く手に入れたいと考えている．ただし，各店では土産物を高々ひとつしか買わない．旅に出る時点で，彼は十分な 1000 円札を持っているが小銭は全く持っていない．また，土産物屋を訪れる順番は変えられない．同じ枚数の 500 円玉を手に入れられるならば，彼はなるべく使うお金を減らしたいと考えている．

例えば，これから訪れる土産物屋での土産物の値段が順に 800 円，700 円，1600 円，600 円だったとしよう．この場合に手に入る 500 円玉の最大枚数は 2 枚であり，その 2 枚を得るのに必要な最低限の出費は 2900 円である．最初の 800 円の土産物を買わず，次の店で 700 円の土産物を 1000 円札で買って 100 円玉 3 枚を手に入れ，その後に残りのふたつを 2100 円と 1100 円を出して買うことで，500 円玉を 2 枚手に入れられる．仮に最初の 800 円の土産物を買ったとすると，500 円玉を 2 枚手に入れるためには少なくとも 1600 円と 600 円の土産物を買わねばならず，結局 3000 円以上の出費となってしまう．

君は彼に，彼の目的を助けるためのプログラムの作成を頼まれた．土産物屋を訪れる順に書かれた土産物の値段のリストを受け取り，最大何枚の 500 円玉を得られるか，及びその枚数を得るのに最低限何円使わなければならないかを答えるプログラムを作って欲しい．

それぞれの支払いに使用できるのは，その時点で持っている 1 円玉，5 円玉，10 円玉，50 円玉，100 円玉の小銭及び（充分にある）1000 円札だけである．支払いの際には，これらの小銭や 1000 円札をいくら出しても構わない．一方，お店は，お釣り，すなわち出されたお金と土産物の価格の差額を，その金額を構成する最小枚数の，1 円玉，5 円玉，10 円玉，50 円玉，100 円玉，500 円玉，及び 1000 円札で返す．無駄な小銭を出して支払いをすることは自由であり，例えば，1000 円の土産物を買う際に 1000 円札と共に 5 枚の 100 円玉を出すことで，お釣りとして 500 円玉を 1 枚手に入れることも可能である．しかし，欲張って小銭を多く出しすぎるのも良くない．1000 円の土産物を買うのに，1000 円札と共に 100 円玉を 10 枚出したとしても，お店は 1000 円札 1 枚を返してくれるだけで 500 円玉 2 枚は手に入らない．

入力は 50 個以下のデータセットからなる．各データセットは次の形式で表される．

n
p₁
...
p_n

n は土産物屋の数であり，100 を超えない正の整数である．p_i は i 番目の土産物屋の土産物の値段である．p_i は，正の整数であり，5000 を超えない．

入力の終わりは，ゼロをひとつ含むだけの行で表される．

各データセットについて、ふたつの整数 c と s をひとつの空白文字で区切って 1 行に出力せよ．c は手に入る 500 円玉の最大枚数であり，s はその枚数の 500 円玉を得るのに必要な土産物の購入金額の合計の最小値である．

4
800
700
1600
600
4
300
700
1600
600
4
300
700
1600
650
3
1000
2000
500
3
250
250
1000
4
1251
667
876
299
0

2 2900
3 2500
3 3250
1 500
3 1500
3 2217

並行処理環境におけるデッドロックとは， 複数のスレッドがお互いにいくつかの資源を使い終わるのを待っていて先に進めないという望ましくない状況を指す． あなたには， 与えられた命令列を複数のスレッドが並行に実行したときにデッドロックが発生する可能性があるか否かを判定するプログラムを作って欲しい．

命令列は '0' から '9' までの数字または 'u' からなる列で， それぞれの文字がひとつの命令を表している． 10 個のスレッドが同じひとつの命令列を実行しようとしており， 各スレッドは命令列の先頭から末尾まで順に命令を実行し， すべての命令を実行し終えると終了する．

数字の命令 k は L₀ から L₉ まで 10 個あるロックと呼ばれる共有資源のうち L_k を獲得する命令である． あるスレッドが L_k を獲得すると， 同じスレッドが 'u' 命令によってロックを解放するまでの間， そのロックはスレッドに保持される． 獲得したスレッド自身も含めすべてのスレッドは， 保持されている状態のロックを新たに獲得することはできない．

より厳密に記述すると，全てのスレッドが終了するまで，以下の処理が繰り返される．

1. まだ終了していないスレッドがひとつ任意に選ばれる．
2. 選ばれたスレッドの次のまだ実行していない命令を実行しようと試みる．
• 次の命令が数字 k であり， ロック L_k がどのスレッドにも保持されていないならば， そのスレッドは命令 k を実行し，ロック L_k を獲得する．
• 次の命令が数字 k であり， ロック L_k が既にどれかのスレッドに保持されていれば， 命令 k は実行されない．
• 次の命令が 'u' であるとき， 命令 'u' を実行し，そのスレッドが保持していたロックをすべて解放する．

このように実行を進めていくと， まだ終了していないスレッドの次に実行する命令が全て， 保持されているロックの獲得命令という状態に陥ることがある． こうなると，以降どのスレッドを選んでも命令が実行されることはない． この状態をデッドロックと呼ぶ．

命令列によっては，スレッドをどのような順番で選んで実行しても決してデッドロックに陥らない． このような命令列は安全であるという． そうでない場合，言い換えるとひとつ以上の実行順序でデッドロックに陥る場合， 命令列は危険であるという． あなたには， 与えられた命令列が安全であるか危険であるかを判定するプログラムを作って欲しい．

入力は 50 個以下のデータセットからなる． 各データセットは次の形式で表される．

n
s

n は命令列の長さ，s は命令列を表す文字列である． n は，正の整数であり，10,000 を超えない． s の各文字は '0' から '9' までの数字または 'u' であり，必ず 'u' で終わる．

入力の終わりは，ゼロだけからなる行で表される．

各データセットについて，与えられた命令列が安全ならば "SAFE"，危険ならば "UNSAFE" と 1 行に出力せよ．

11
01u12u0123u
6
01u10u
8
201u210u
9
01u12u20u
3
77u
12
9u8u845u954u
0

SAFE
UNSAFE
SAFE
UNSAFE
UNSAFE
UNSAFE

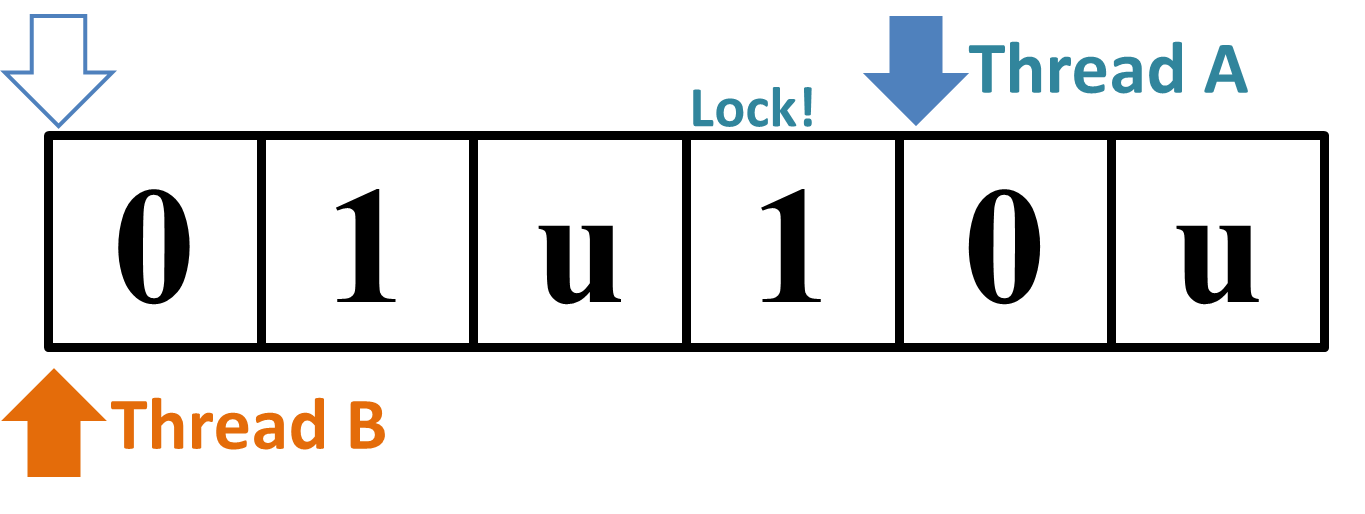
2 番目の入力 "01u10u" はデッドロックとなる可能性がある． ひとつのスレッドが最初の 4 命令 "01u1" を続けて実行した場合， このスレッドはロック L₁ を保持している． この状態で別のスレッドが最初の命令 '0' を実行すると，こちらのスレッドは L₀ を獲得する． こうなると，ひとつ目のスレッドは既にふたつ目のスレッドに保持されている L₀ を獲得しようとする． 一方，ふたつ目のスレッドはひとつ目のスレッドに保持されている L₁ を獲得しようとする．結果，デッドロックが発生する．

→ →
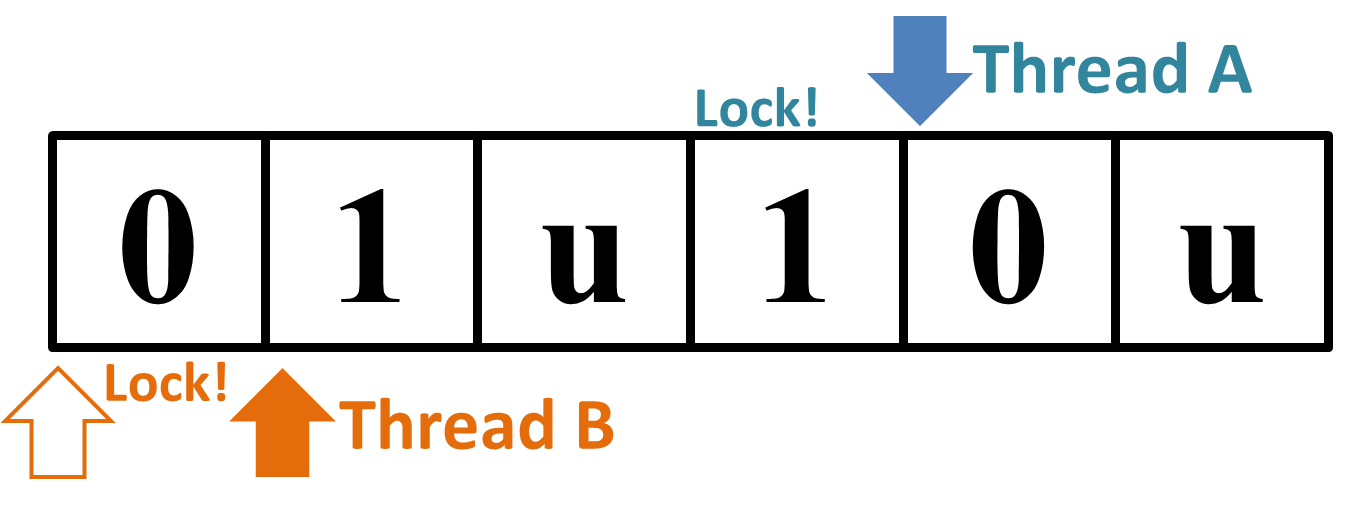
図1: Sample Input 2 "01u10u" が危険な理由．

一方で，3 番目の入力 "201u210u" は安全である． ひとつのスレッドが "201u21" を実行し，もう一方が "20" を実行するとデッドロックになると考えるかもしれないが， この状況は決して発生しない．なぜなら，ロック L₂ をふたつのスレッドが同時に保持することはないからである．

多くの小島からなる市があり，市民はそれらの島に住んでいる． 島から島へ渡るにはフェリーを使うしかなく，多くの市民は不便に感じている． そこで市長はすべての島を互いに行き来できるように橋を架けることにした．

市にはふたつの建設会社（A社とB社）がある． 市長がこれらに見積もりを請求し，いくつかの提案を次の形で得た： 「建設会社 A (または B) は島 u と島 v の間を結ぶ橋を w 億円で建造できる」．

市長はこれらの提案のうちいくつかを採用することで最も安い建造計画を作ろうとしている． ところが，もし市長が一方の会社の提案を多く採用すると，もう一方の会社は潰れてしまう． これはたったふたつしか建設会社がない市にとっては望ましくない． しかし一方で，無駄な建設だという批判を避けるには，全ての島を行き来できるようにするために必要最低限の本数の橋 (すなわち n−1 本の橋) しか採用できない． そこで，市長は予め建設会社 A の提案を丁度 k 個，建設会社 B の提案を丁度 n−1−k 個採用することに決めた．

あなたの仕事は，条件を満たす中で最も安い計画の費用を計算するプログラムを作ることである． ここで，計画の費用とは採用されるすべての提案の費用の合計のことをいう．

入力は複数のデータセットからなる． データセットの数は 30 以下である． 各データセットは次の形式で表される．

n m k
u₁ v₁ w₁ l₁
...
u_m v_m w_m l_m

最初の行にはみっつの整数 n, m, k が含まれており，それぞれ n は島の数，m は提案の総数，k は A 社から採用する提案の数を意味する (2 ≤ n ≤ 200, 1 ≤ m ≤ 600, 0 ≤ k ≤ n−1)． 島は 1 から n までの整数で表されている． 続く m 行は提案の情報を示しており，各提案はみっつの整数 u_i, v_i, w_i とひとつの文字 l_i によって表されている．ここで u_i と v_i は橋の両端の島，w_i はその橋を架ける値段（億円）， そして l_i は見積もりを提出した建設会社の名前を意味している (1 ≤ u_i ≤ n, 1 ≤ v_i ≤ n, 1 ≤ w_i ≤ 100, l_i = 'A' または 'B')． 橋は相異なる島を結ぶものとしてよい，すなわち u_i ≠ v_i である． また，各会社は島の対に対して高々ひとつの提案を出すものとしてよい，すなわち i ≠ j かつ l_i = l_j のとき {u_i, v_i} ≠ {u_j, v_j} である．

入力の終わりは，空白ひとつで区切られたゼロみっつからなる行で表される．

各データセットについて，条件を満たす一番安い計画の費用（億円）を出力せよ． 条件を満たす計画が存在しない場合は −1 と出力すること．

4 5 2
1 2 2 A
1 3 2 A
1 4 2 A
2 3 1 B
3 4 1 B
5 8 2
1 2 1 A
2 3 1 A
3 4 3 A
4 5 3 A
1 2 5 B
2 3 5 B
3 4 8 B
4 5 8 B
5 5 1
1 2 1 A
2 3 1 A
3 4 1 A
4 5 1 B
3 5 1 B
4 5 3
1 2 2 A
2 4 3 B
3 4 4 B
2 3 5 A
3 1 6 A
0 0 0

5
16
-1
-1

折り紙の権威で，国際紙細工文化協会（Intercultural Consortium on Paper Crafts）の理事でもある G 博士は， 折り紙は作られる図形が複雑なほど美しいという信念を持っている． あなたは博士の助手として，最も複雑な形が得られる折り方を見つけなければならない． 博士が言うには，図形の複雑さとは，頂点の個数が多いことであり， 頂点数が同じ場合には周長が長いことである． ただし，問題を簡単にするため，凸多角形を一度だけ折る場合について考え， 紙を折るときには必ずある頂点が別の頂点に重なるように折らなければならないものとする．

凸多角形が与えられたとき， 一度だけ折り返してできる多角形の中で， 最も複雑なものの周長を出力するプログラムを書け．

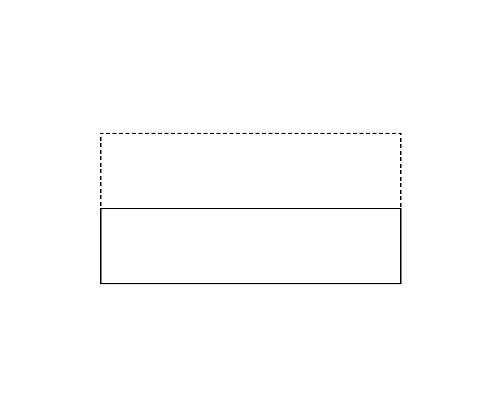
図1左は，Sample Input の最初のデータセットに記述された多角形で，長方形である． これを折ると図1-a〜c の実線で示すように 3 通りの多角形を作ることができる． このデータセットに対しては， この中で最も頂点数の多い五角形（図1-a）の周長を答えればよい． 図1-a よりも図1-b の長方形の方が周長は長いが，頂点数の多い方が優先される．

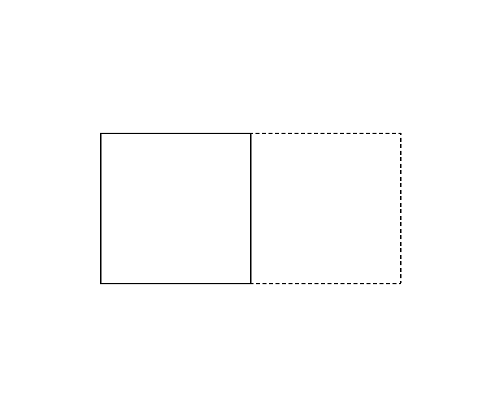	(a)	(b)	(c)

図1: 第1サンプルインプットの場合

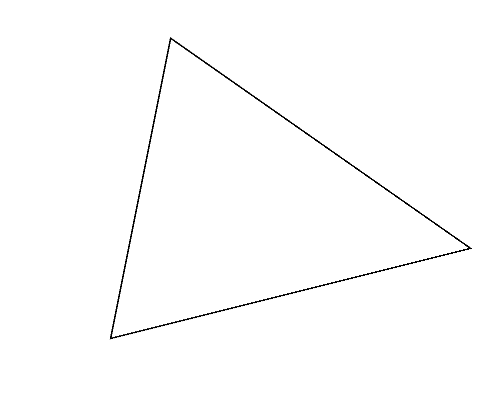
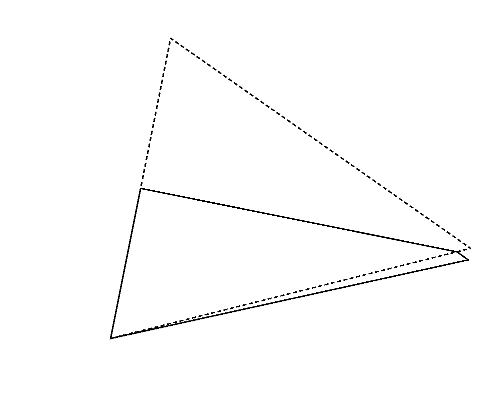
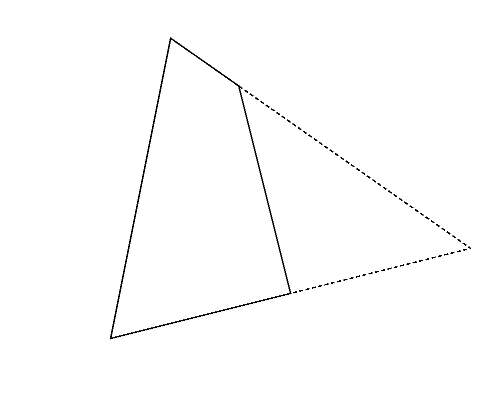
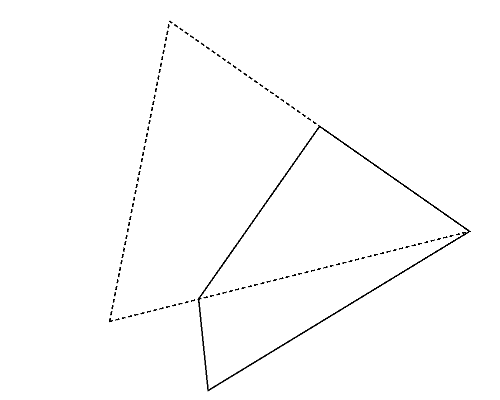
図2左は，Sample Input の 2 番目のデータセットに記述された多角形で，三角形である． この三角形は，どのように 2 頂点を選んでも， それらを重ねるように折ると四角形（図2-a〜c）になる． これらの中から，最も長い周長（この場合は 図2-a の周長）を答えればよい．

	(a)	(b)	(c)

図2: 第2サンプルインプットの場合

入力として与えられる多角形は凸に限られるが， これを折って得られる多角形は凹であるかもしれない． 図3左は，Sample Input の 3 番目のデータセットに記述された多角形である． この多角形は，折ると凹六角形になる場合（図3右）があり， このとき最も頂点数が多くなる．

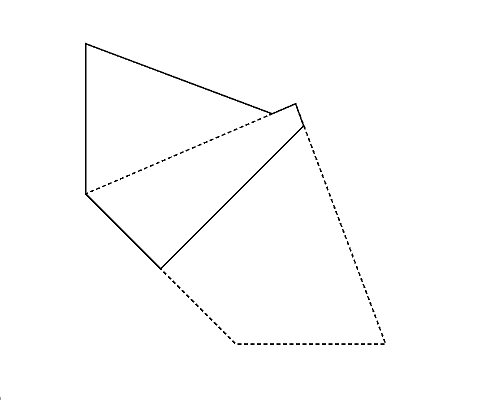
図3: 第3サンプルインプットの場合

図4左は，Sample Input の 5 番目のデータセットに記述された多角形である． 図4-bの図形は図4-aの図形よりも周長が長いが，図4-bの図形は四角形であるので，正解は図4-aの五角形の周長となる．

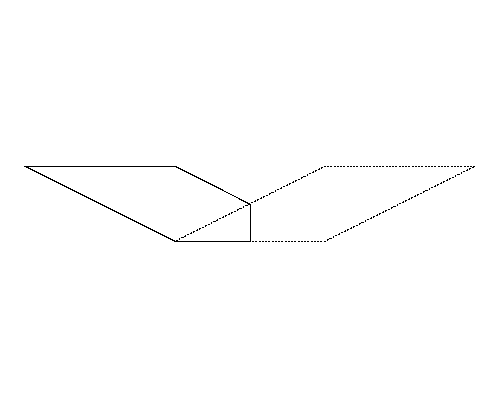	(a)	(b)

図4: 第5サンプルインプットの場合

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
x₁ y₁
...
x_n y_n

ここで n は最初に与えられる多角形の頂点数であり， 3 ≤ n ≤ 20 を満たす正整数である． x_iとy_iは 0 ≤ x_i,y_i < 1000 を満たす整数で， (x_i, y_i) は i 番目の頂点の座標を与える． また，頂点の列 (x₁, y₁), ..., (x_n, y_n) は y 軸を上向きとする xy 平面上で反時計回りに順番に並んでおり， こうして与えられる多角形が凸であることは保証されている．

ここで入力に与えられる多角形の任意の 2 頂点を重ねるように折って得られる多角形について， 以下のふたつの条件が成り立つものと仮定してよい．

• 多角形の頂点間の距離は，いずれも 0.00001 以上である．
• 多角形の連続する 3 頂点 P, Q, R について，点 Q と点 P, R を通る直線との距離は 0.00001 以上である．

入力の終わりは，ゼロだけからなる行で表される．

各データセットについて，与えられた多角形を折ることで得られる多角形で最も複雑なものの周長を出力せよ． 出力には 0.00001 以上の誤差を含んではならない． それ以外の余計な文字を出力してはならない．

4
0 0
10 0
10 5
0 5
3
5 0
17 3
7 10
4
0 5
5 0
10 0
7 8
4
0 0
40 0
50 5
0 5
4
0 0
10 0
20 5
10 5
7
4 0
20 0
24 1
22 10
2 10
0 6
0 4
18
728 997
117 996
14 988
1 908
0 428
2 98
6 54
30 28
106 2
746 1
979 17
997 25
998 185
999 573
999 938
995 973
970 993
910 995
6
0 40
0 30
10 0
20 0
40 70
30 70
0

23.090170
28.528295
23.553450
97.135255
34.270510
57.124116
3327.900180
142.111776

あなたは研究所で小型飛行ロボットを開発している．

研究所は K 階建ての直方体状の建物であり，下の階から順に 1 から K の番号がついている． それぞれの階の床は各辺が東西方向または南北方向に対して平行な正方形であり， それらの床は R × R 個のセルに分割されている． z 階の，西から x 番目の列の南から y 番目にあるセルを (x, y, z) で表す（x, y は 1 始まりとする）． それぞれの x, y, z (z > 1) に対し，セル (x, y, z) はセル (x, y, z − 1) の真上にある．

研究所内では N 個のロボットが飛行している． それぞれのロボットには 1 から N までの番号が付けられている． 最初，i 番目のロボットはセル (x_i, y_i, z_i) にいる．

あなたはこれまでの苦労により，それぞれの飛行ロボットを思い通りの場所に移動させる機能を無事実装した． そこで次にあなたは，ロボットの現在の位置と周囲の環境をもとにして，すべてのロボットをどこかひとつのセルに最小のエネルギー消費で集める機能を新たに実装しようと考えた．

2 階以上の床にはいくつか穴が開いている． 穴は長方形状で，穴のそれぞれの辺はセルの辺に沿った位置にある． 穴は全部で M 個あり，それぞれ 1 から M の番号が付けられている． j 番目の穴の情報は五つの整数 u_1j, v_1j, u_2j, v_2j, w_j で表される． j 番目の穴はセル (x, y, w_j) (u_1j ≤ x ≤ u_2j, v_1j ≤ y ≤ v_2j) を含んでいる．

ロボットの可能な動きとそれに伴うエネルギー消費量は以下のとおりである．

• ロボットのいるセルから東西南北の 4 方向で隣り合うセルに移動することができる． この移動には 1 のエネルギーを消費する．
• もしロボットのいるセルの真上が穴に含まれているならば，ロボットを真上のセルに移動させることができる．この移動には 100 のエネルギーを消費する．

ロボットは，下に穴があっても落下することはないものとする． また，ふたつ以上のロボットを同じセルに移動させても良いものとする．

あなたはいま，飛んでいる全てのロボットを穴に含まれていない K 階のセルに最小のエネルギーで集めたい． ロボットの消費するエネルギーの合計値の最小値を計算し，出力せよ．

入力は 32 個以下のデータセットからなる． 各データセットは次の形式で表される． 入力に現れる値は全て整数である．

N
M K R
x₁ y₁ z₁
...
x_N y_N z_N
u₁₁ v₁₁ u₂₁ v₂₁ w₁
...
u_1M v_1M u_2M v_2M w_M

N は研究所にあるロボットの個数 (1 ≤ N ≤ 100) である． M は穴の個数 (1 ≤ M ≤ 50)， K は研究所の階数 (2 ≤ K ≤ 10)， R は各階の 1 行及び 1 列のセルの個数 (3 ≤ R ≤ 1,000,000) である．

各 i に対し，x_i, y_i, z_i は i 番目のロボットが最初にいるセル (1 ≤ x_i ≤ R, 1 ≤ y_i ≤ R, 1 ≤ z_i ≤ K) を表す． また，各 j に対し， u_1j, v_1j, u_2j, v_2j, w_j は j 番目の穴の位置と範囲 (1 ≤ u_1j ≤ u_2j ≤ R, 1 ≤ v_1j ≤ v_2j ≤ R, 2 ≤ w_j ≤ K) を表す．

入力について以下のことが保証される．

• 2 階以上のどの階にも少なくともひとつは穴が存在する．
• どの階にも，穴に含まれないセルが少なくともひとつは存在する．
• どのふたつの穴の範囲も重ならない．すなわち，どのセルも高々ひとつの穴にしか含まれない．

二個以上のロボットが最初に同じ階の同じセルにいることはありうる． また，隣接するふたつのセルがそれぞれ異なる穴に含まれるということもありうる．

入力の終わりは，ひとつのゼロだけからなる行で表される．

合計エネルギー消費の最小値を 1 行に出力せよ．

2
1 2 8
1 1 1
8 8 1
3 3 3 3 2
3
3 2 3
1 1 2
1 1 2
1 1 2
1 1 1 1 2
1 2 1 2 2
2 1 2 1 2
2
2 3 100
100 50 1
1 50 3
100 1 100 100 3
1 1 1 100 2
5
6 7 60
11 11 1
11 51 1
51 11 1
51 51 1
31 31 1
11 11 51 51 2
11 11 51 51 3
11 11 51 51 4
11 11 51 51 5
18 1 54 42 6
1 43 59 60 7
5
6 4 9
5 5 3
1 1 1
1 9 1
9 1 1
9 9 1
3 3 7 7 4
4 4 6 6 2
1 1 2 2 3
1 8 2 9 3
8 1 9 2 3
8 8 9 9 3
5
10 5 50
3 40 1
29 13 2
39 28 1
50 50 1
25 30 5
3 5 10 10 2
11 11 14 14 2
15 15 20 23 2
40 40 41 50 2
1 49 3 50 2
30 30 50 50 3
1 1 10 10 4
1 30 1 50 5
20 30 20 50 5
40 30 40 50 5
15
2 2 1000000
514898 704203 1
743530 769450 1
202298 424059 1
803485 898125 1
271735 512227 1
442644 980009 1
444735 799591 1
474132 623298 1
67459 184056 1
467347 302466 1
477265 160425 2
425470 102631 2
547058 210758 2
52246 779950 2
291896 907904 2
480318 350180 768473 486661 2
776214 135749 872708 799857 2
0

216
6
497
3181
1365
1930
6485356