Dr. Tsukuba has devised a new method of programming training. In order to evaluate the effectiveness of this method, he plans to carry out a control experiment. Having two students as the participants of the experiment, one of them will be trained under the conventional method and the other under his new method. Comparing the final scores of these two, he will be able to judge the effectiveness of his method.

It is important to select two students having the closest possible scores, for making the comparison fair. He has a list of the scores of all students who can participate in the experiment. You are asked to write a program which selects two of them having the smallest difference in their scores.

The input consists of multiple datasets, each in the following format.

n
a₁ a₂ … a_n

A dataset consists of two lines. The number of students n is given in the first line. n is an integer satisfying 2 ≤ n ≤ 1000. The second line gives scores of n students. a_i (1 ≤ i ≤ n) is the score of the i-th student, which is a non-negative integer not greater than 1,000,000.

The end of the input is indicated by a line containing a zero. The sum of n's of all the datasets does not exceed 50,000.

For each dataset, select two students with the smallest difference in their scores, and output in a line (the absolute value of) the difference.

5
10 10 10 10 10
5
1 5 8 9 11
7
11 34 83 47 59 29 70
0

0
1
5

The citizens of TKB City are famous for their deep love in elections and vote counting. Today they hold an election for the next chairperson of the electoral commission. Now the voting has just been closed and the counting is going to start. The TKB citizens have strong desire to know the winner as early as possible during vote counting.

The election candidate receiving the most votes shall be the next chairperson. Suppose for instance that we have three candidates A, B, and C and ten votes. Suppose also that we have already counted six of the ten votes and the vote counts of A, B, and C are four, one, and one, respectively. At this moment, every candidate has a chance to receive four more votes and so everyone can still be the winner. However, if the next vote counted is cast for A, A is ensured to be the winner since A already has five votes and B or C can have at most four votes at the end. In this example, therefore, the TKB citizens can know the winner just when the seventh vote is counted.

Your mission is to write a program that receives every vote counted, one by one, identifies the winner, and determines when the winner gets ensured.

The input consists of at most 1500 datasets, each consisting of two lines in the following format.

n
c₁ c₂ … c_n

n in the first line represents the number of votes, and is a positive integer no greater than 100. The second line represents the n votes, separated by a space. Each c_i (1 ≤ i ≤ n) is a single uppercase letter, i.e. one of 'A' through 'Z'. This represents the election candidate for which the i-th vote was cast. Counting shall be done in the given order from c₁ to c_n.

You should assume that at least two stand as candidates even when all the votes are cast for one candidate.

The end of the input is indicated by a line containing a zero.

For each dataset, unless the election ends in a tie, output a single line containing an uppercase letter c and an integer d separated by a space: c should represent the election winner and d should represent after counting how many votes the winner is identified. Otherwise, that is, if the election ends in a tie, output a single line containing `TIE'.

1
A
4
A A B B
5
L M N L N
6
K K K K K K
6
X X X Y Z X
10
A A A B A C A C C B
10
U U U U U V V W W W
0

A 1
TIE
TIE
K 4
X 5
A 7
U 8

The bamboos live for decades, and at the end of their lives, they flower to make their seeds. Dr. ACM, a biologist, was fascinated by the bamboos in blossom in his travel to Tsukuba. He liked the flower so much that he was tempted to make a garden where the bamboos bloom annually. Dr. ACM started research of improving breed of the bamboos, and finally, he established a method to develop bamboo breeds with controlled lifetimes. With this method, he can develop bamboo breeds that flower after arbitrarily specified years.

Let us call bamboos that flower k years after sowing "k-year-bamboos." k years after being sowed, k-year-bamboos make their seeds and then die, hence their next generation flowers after another k years. In this way, if he sows seeds of k-year-bamboos, he can see bamboo blossoms every k years. For example, assuming that he sows seeds of 15-year-bamboos, he can see bamboo blossoms every 15 years; 15 years, 30 years, 45 years, and so on, after sowing.

Dr. ACM asked you for designing his garden. His garden is partitioned into blocks, in each of which only a single breed of bamboo can grow. Dr. ACM requested you to decide which breeds of bamboos should he sow in the blocks in order to see bamboo blossoms in at least one block for as many years as possible.

You immediately suggested to sow seeds of one-year-bamboos in all blocks. Dr. ACM, however, said that it was difficult to develop a bamboo breed with short lifetime, and would like a plan using only those breeds with long lifetimes. He also said that, although he could wait for some years until he would see the first bloom, he would like to see it in every following year. Then, you suggested a plan to sow seeds of 10-year-bamboos, for example, in different blocks each year, that is, to sow in a block this year and in another block next year, and so on, for 10 years. Following this plan, he could see bamboo blossoms in one block every year except for the first 10 years. Dr. ACM objected again saying he had determined to sow in all blocks this year.

After all, you made up your mind to make a sowing plan where the bamboos bloom in at least one block for as many consecutive years as possible after the first m years (including this year) under the following conditions:

• the plan should use only those bamboo breeds whose lifetimes are m years or longer, and
• Dr. ACM should sow the seeds in all the blocks only this year.

The input consists of at most 50 datasets, each in the following format.

m n

An integer m (2 ≤ m ≤ 100) represents the lifetime (in years) of the bamboos with the shortest lifetime that Dr. ACM can use for gardening. An integer n (1 ≤ n ≤ 500,000) represents the number of blocks.

The end of the input is indicated by a line containing two zeros.

No matter how good your plan is, a "dull-year" would eventually come, in which the bamboos do not flower in any block. For each dataset, output in a line an integer meaning how many years from now the first dull-year comes after the first m years.

Note that the input of m = 2 and n = 500,000 (the last dataset of the Sample Input) gives the largest answer.

3 1
3 4
10 20
100 50
2 500000
0 0

4
11
47
150
7368791

You are playing a variant of a game called "Daruma Otoshi (Dharma Block Striking)".

At the start of a game, several wooden blocks of the same size but with varying weights are stacked on top of each other, forming a tower. Another block symbolizing Dharma is placed atop. You have a wooden hammer with its head thicker than the height of a block, but not twice that.

You can choose any two adjacent blocks, except Dharma on the top, differing at most 1 in their weight, and push both of them out of the stack with a single blow of your hammer. The blocks above the removed ones then fall straight down, without collapsing the tower. You cannot hit a block pair with weight difference of 2 or more, for that makes too hard to push out blocks while keeping the balance of the tower. There is no chance in hitting three blocks out at a time, for that would require superhuman accuracy.

The goal of the game is to remove as many blocks as you can. Your task is to decide the number of blocks that can be removed by repeating the blows in an optimal order.

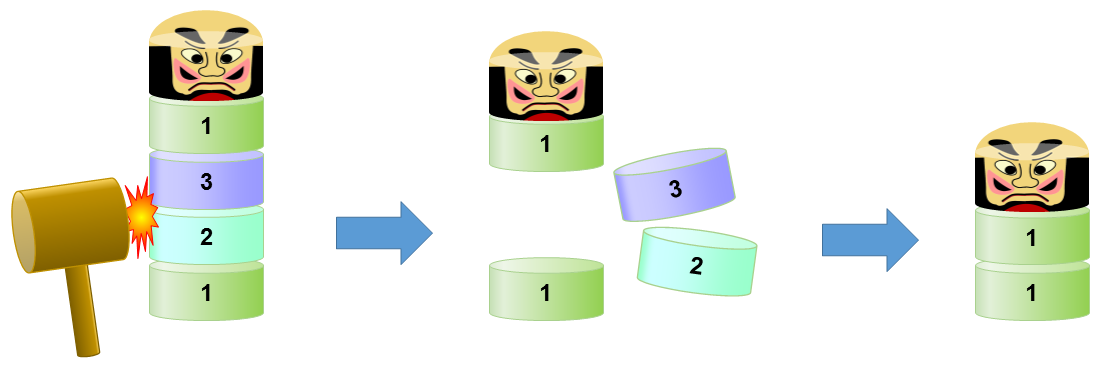
Figure D1. Striking out two blocks at a time

In the above figure, with a stack of four blocks weighing 1, 2, 3, and 1, in this order from the bottom, you can hit middle two blocks, weighing 2 and 3, out from the stack. The blocks above will then fall down, and two blocks weighing 1 and the Dharma block will remain. You can then push out the remaining pair of weight-1 blocks after that.

The input consists of multiple datasets. The number of datasets is at most 50. Each dataset is in the following format.

n
w₁ w₂ … w_n

n is the number of blocks, except Dharma on the top. n is a positive integer not exceeding 300. w_i gives the weight of the i-th block counted from the bottom. w_i is an integer between 1 and 1000, inclusive.

The end of the input is indicated by a line containing a zero.

For each dataset, output in a line the maximum number of blocks you can remove.

4
1 2 3 4
4
1 2 3 1
5
5 1 2 3 6
14
8 7 1 4 3 5 4 1 6 8 10 4 6 5
5
1 3 5 1 3
0

4
4
2
12
0

We are designing an installation art piece consisting of a number of cubes with 3D printing technology for submitting one to Installation art Contest with Printed Cubes (ICPC). At this time, we are trying to model a piece consisting of exactly k cubes of the same size facing the same direction.

First, using a CAD system, we prepare n (n ≥ k) positions as candidates in the 3D space where cubes can be placed. When cubes would be placed at all the candidate positions, the following three conditions are satisfied.

• Each cube may overlap zero, one or two other cubes, but not three or more.
• When a cube overlap two other cubes, those two cubes do not overlap.
• Two non-overlapping cubes do not touch at their surfaces, edges or corners.

Second, choosing appropriate k different positions from n candidates and placing cubes there, we obtain a connected polyhedron as a union of the k cubes. When we use a 3D printer, we usually print only the thin surface of a 3D object. In order to save the amount of filament material for the 3D printer, we want to find the polyhedron with the minimal surface area.

Your job is to find the polyhedron with the minimal surface area consisting of k connected cubes placed at k selected positions among n given ones.

Figure E1. A polyhedron formed with connected identical cubes.

The input consists of multiple datasets. The number of datasets is at most 100. Each dataset is in the following format.

n k s
x₁ y₁ z₁
...
x_n y_n z_n

In the first line of a dataset, n is the number of the candidate positions, k is the number of the cubes to form the connected polyhedron, and s is the edge length of cubes. n, k and s are integers separated by a space. The following n lines specify the n candidate positions. In the i-th line, there are three integers x_i, y_i and z_i that specify the coordinates of a position, where the corner of the cube with the smallest coordinate values may be placed. Edges of the cubes are to be aligned with either of three axes. All the values of coordinates are integers separated by a space. The three conditions on the candidate positions mentioned above are satisfied.

The parameters satisfy the following conditions: 1 ≤ k ≤ n ≤ 2000, 3 ≤ s ≤ 100, and -4×10⁷ ≤ x_i, y_i, z_i ≤ 4×10⁷.

The end of the input is indicated by a line containing three zeros separated by a space.

For each dataset, output a single line containing one integer indicating the surface area of the connected polyhedron with the minimal surface area. When no k cubes form a connected polyhedron, output -1.

1 1 100
100 100 100
6 4 10
100 100 100
106 102 102
112 110 104
104 116 102
100 114 104
92 107 100
10 4 10
-100 101 100
-108 102 120
-116 103 100
-124 100 100
-132 99 100
-92 98 100
-84 100 140
-76 103 100
-68 102 100
-60 101 100
10 4 10
100 100 100
108 101 100
116 102 100
124 100 100
132 102 100
200 100 103
192 100 102
184 100 101
176 100 100
168 100 103
4 4 10
100 100 100
108 94 100
116 100 100
108 106 100
23 6 10
100 100 100
96 109 100
100 118 100
109 126 100
118 126 100
127 118 98
127 109 104
127 100 97
118 91 102
109 91 100
111 102 100
111 102 109
111 102 118
111 102 91
111 102 82
111 114 96
111 114 105
102 114 114
93 114 114
84 114 105
84 114 96
93 114 87
102 114 87
10 3 10
100 100 100
116 116 102
132 132 104
148 148 106
164 164 108
108 108 108
124 124 106
140 140 104
156 156 102
172 172 100
0 0 0

60000
1856
-1
1632
1856
2796
1640

Image data which are left by a mysterious syndicate were discovered. You are requested to analyze the data. The syndicate members used characters invented independently. A binary image corresponds to one character written in black ink on white paper.

Although you found many variant images that represent the same character, you discovered that you can judge whether or not two images represent the same character with the surrounding relation of connected components. We present some definitions as follows. Here, we assume that white pixels fill outside of the given image.

• White connected component : A set of white pixels connected to each other horizontally or vertically (see below).
• Black connected component : A set of black pixels connected to each other horizontally, vertically, or diagonally (see below).
• Connected component : A white or a black connected component.
• Background component : The connected component including pixels outside of the image. Any white pixels on the periphery of the image are thus included in the background component.

connected	disconnected	connected	connected
Connectedness of white pixels		Connectedness of black pixels

Let C₁ be a connected component in an image and C₂ be another connected component in the same image with the opposite color. Let's think of a modified image in which colors of all pixels not included in C₁ nor C₂ are changed to that of C₂. If neither C₁ nor C₂ is the background component, the color of the background component is changed to that of C₂. We say that C₁ surrounds C₂ in the original image when pixels in C₂ are not included in the background component in the modified image. (see below)

Two images represent the same character if both of the following conditions are satisfied.

• The two images have the same number of connected components.
• Let S and S' be the sets of connected components of the two images. A bijective function f : S → S' satisfying the following conditions exists.
• For each connected component C that belongs to S, f (C) has the same color as C.
• For each of C₁ and C₂ belonging to S, f (C₁) surrounds f (C₂) if and only if C₁ surrounds C₂.

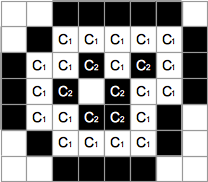
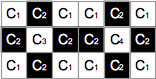
Let's see an example. Connected components in the images of the figure below has the following surrounding relations.

• C₁ surrounds C₂.
• C₂ surrounds C₃.
• C₂ surrounds C₄.
• C'₁ surrounds C'₂.
• C'₂ surrounds C'₃.
• C'₂ surrounds C'₄.

A bijective function defined as f (C_i) = C'_i for each connected component satisfies the conditions stated above. Therefore, we can conclude that the two images represent the same character.

Make a program judging whether given two images represent the same character.

The input consists of at most 200 datasets. The end of the input is represented by a line containing two zeros. Each dataset is formatted as follows.

image 1
image 2

Each image has the following format.

h w
p_(1,1) ... p_(1,w)
...
p_(h,1) ... p_(h,w)

h and w are the height and the width of the image in numbers of pixels. You may assume that 1 ≤ h ≤ 100 and 1 ≤ w ≤ 100. Each of the following h lines consists of w characters. p_(y,x) is a character representing the color of the pixel in the y-th row from the top and the x-th column from the left. Characters are either a period (".") meaning white or a sharp sign ("#") meaning black.

For each dataset, output "yes" if the two images represent the same character, or output "no", otherwise, in a line. The output should not contain extra characters.

3 6
.#..#.
#.##.#
.#..#.
8 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#..#..#
.#####.
...#...
3 3
#..
...
#..
3 3
#..
.#.
#..
3 3
...
...
...
3 3
...
.#.
...
3 3
.#.
#.#
.#.
3 3
.#.
###
.#.
7 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#.....#
.#####.
7 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#..#..#
.#####.
7 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#.....#
.#####.
7 11
.#####.....
#.....#....
#..#..#..#.
#.#.#.#.#.#
#..#..#..#.
#.....#....
.#####.....
7 3
.#.
#.#
.#.
#.#
.#.
#.#
.#.
7 7
.#####.
#..#..#
#..#..#
#.#.#.#
#..#..#
#..#..#
.#####.
3 1
#
#
.
1 2
#.
0 0

yes
no
no
no
no
no
yes
yes

The warp drive technology is reforming air travel, making the travel times drastically shorter. Aircraft reaching above the warp fields built on the ground surface can be transferred to any desired destination in a twinkling.

With the current immature technology, however, building warp fields is quite expensive. Our budget allows building only two of them. Fortunately, the cost does not depend on the locations of the warp fields, and we can build them anywhere on the ground surface, even at an airport.

Your task is, given locations of airports and a list of one way flights among them, find the best locations to build the two warp fields that give the minimal average cost. The average cost is the root mean square of travel times of all the flights, defined as follows.

Here, m is the number of flights and t_j is the shortest possible travel time of the j-th flight. Note that the value of t_j depends on the locations of the warp fields.

For simplicity, we approximate the surface of the ground by a flat two dimensional plane, and approximate airports, aircraft, and warp fields by points on the plane. Different flights use different aircraft with possibly different cruising speeds. Times required for climb, acceleration, deceleration and descent are negligible. Further, when an aircraft reaches above a warp field, time required after that to its destination is zero. As is explained below, the airports have integral coordinates. Note, however, that the warp fields can have non-integer coordinates.

The input consists of at most 35 datasets, each in the following format.

n m
x₁ y₁
...
x_n y_n
a₁ b₁ v₁
...
a_m b_m v_m

n is the number of airports, and m is the number of flights (2 ≤ n ≤ 20, 2 ≤ m ≤ 40). For each i, x_i and y_i are the coordinates of the i-th airport. x_i and y_i are integers with absolute values at most 1000. For each j, a_j and b_j are integers between 1 and n inclusive, and are the indices of the departure and arrival airports for the j-th flight, respectively. v_j is the cruising speed for the j-th flight, that is, the distance that the aircraft of the flight moves in one time unit. v_j is a decimal fraction with two digits after the decimal point (1 ≤ v_j ≤ 10).

The following are guaranteed.

• Two different airports have different coordinates.
• The departure and arrival airports of any of the flights are different.
• Two different flights have different departure airport and/or arrival airport.

The end of the input is indicated by a line containing two zeros.

For each dataset, output the average cost when you place the two warp fields optimally. The output should not contain an absolute error greater than 10^-6.

3 4
100 4
100 0
0 0
1 2 1.00
2 1 1.00
3 1 9.99
3 2 9.99
7 6
0 0
1 0
2 0
0 10
1 10
2 10
20 5
1 7 1.00
2 7 1.00
3 7 1.00
4 7 1.00
5 7 1.00
6 7 1.00
4 4
-1 -1
1 -1
-1 1
1 1
1 4 1.10
4 2 2.10
2 3 3.10
3 1 4.10
8 12
-91 0
-62 0
-18 0
2 0
23 0
55 0
63 0
80 0
2 7 3.96
3 2 2.25
2 4 5.48
8 7 9.74
5 6 6.70
7 6 1.51
4 1 7.41
5 8 1.11
6 3 2.98
3 4 2.75
1 8 5.89
4 5 5.37
0 0

1.414214
0.816497
0.356001
5.854704

A gift exchange party will be held at a school in TKB City.

For every pair of students who are close friends, one gift must be given from one to the other at this party, but not the other way around. It is decided in advance the gift directions, that is, which student of each pair receives a gift. No other gift exchanges are made.

If each pair randomly decided the gift direction, some might receive countless gifts, while some might receive only few or even none.

You'd like to decide the gift directions for all the friend pairs that minimize the difference between the smallest and the largest numbers of gifts received by a student. Find the smallest and the largest numbers of gifts received when the difference between them is minimized. When there is more than one way to realize that, find the way that maximizes the smallest number of received gifts.

The input consists of at most 10 datasets, each in the following format.

n m
u₁ v₁
...
u_m v_m

n is the number of students, and m is the number of friendship relations (2 ≤ n ≤ 100, 1 ≤ m ≤ n (n-1)/2). Students are denoted by integers between 1 and n, inclusive. The following m lines describe the friendship relations: for each i, student u_i and v_i are close friends (u_i < v_i). The same friendship relations do not appear more than once.

The end of the input is indicated by a line containing two zeros.

For each dataset, output a single line containing two integers l and h separated by a single space. Here, l and h are the smallest and the largest numbers, respectively, of gifts received by a student.

3 3
1 2
2 3
1 3
4 3
1 2
1 3
1 4
4 6
1 2
1 3
1 4
2 3
3 4
2 4
0 0

1 1
0 1
1 2