筑波博士は，プログラミング教育の新しい方法を考案した． この方法が有効かどうかを確認するために，対照実験を行うことにした． 2 人の学生を被験者として，一方を従来の方法で教え，もう一方を新しい方法で教える． 2 人の最終的な成績を比べれば，新しい方法が有効かどうか判定できるだろう．

公平な比較を行うためには，成績のなるべく近い 2 人を選ぶことが肝要である． 手元には，実験に参加可能な学生各人の成績の一覧表がある． この中から成績の差が最も小さい 2 人を選ぶプログラムを書いてほしい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
a₁ a₂ … a_n

データセットは 2 行からなる． 1 行目には学生の人数 n が与えられる． n は整数であり，2 ≤ n ≤ 1000 が成り立つ． 2 行目には n 人の学生の成績が与えられる． a_i（1 ≤ i ≤ n）が i 番目の学生の成績である． この値は整数であり，0 以上 1,000,000 以下である．

入力の終わりは，1 個のゼロだけからなる行で表される． 全データセットの n の合計は 50,000 を超えない．

各データセットについて，成績の差が最小の 2 人の学生を選び， その差（の絶対値）を 1 行に出力せよ．

5
10 10 10 10 10
5
1 5 8 9 11
7
11 34 83 47 59 29 70
0

0
1
5

TKB 市民は選挙と開票が大好きなことで有名である． 今日は選挙管理委員会の次期委員長を決める選挙の日である． 今投票が終わり，開票が始まろうとしている． TKB 市民は，開票中に少しでも早く当選者を知りたいと強く望んでいる．

もっとも多くの票を得た候補者が次期委員長に選出される． たとえば，候補者が A, B, C の 3 人で，投票数が 10 票の場合を考える． そして，10 票のうち 6 票までの開票が行われ，A, B, C がそれぞれ 4 票，1 票，1 票を得たとする． この時点では，すべての候補者があと 4 票を得る可能性があり，全員が当選する可能性を残している． しかし，もし次に開いた票が A に投じられたものなら，A の当選が確定する． なぜならば，ここまでの A の得票は 5 票となり，最終的な B と C それぞれの得票は，高々 4 票にしかならないからである． この例では，7 票目を開票した時点で，TKB 市民は当選者を知ることができる．

そこで，開票中の票を一つずつ順番に受け取り，当選者が誰であるかとそれがいつ確定したかを求めるプログラムを作成してほしい．

入力は最大で 1500 個のデータセットからなる． 各データセットは 2 行からなり次のような形式である．

n
c₁ c₂ … c_n

1 行目の整数 n は投票数を表し，100 以下の正整数である． 2 行目が投票された n 票を表す． 各 c_i（1 ≤ i ≤ n）は，一つの英大文字（'A' から 'Z' のうちの一つ）であり，空白文字で区切られる． これは i 番目の票が投じられた候補者を表す． 開票は，c₁ から c_n まで出現順に行われる．

たとえ，すべての票が一人の候補者に集中していても，候補者は二人以上いると仮定すること．

入力の終わりは，1 個のゼロだけからなる行で表される．

各データセットについて，選挙が引き分けに終わらないなら，空白文字 1 個で区切られた英大文字 c と整数 d からなる行を出力せよ． ここで，c は当選者を表す． d は何番目の票を開票した時点ではじめて当選が確定したかを表す． それ以外の場合，すなわち選挙が引き分けに終わった場合は，`TIE' のみからなる行を出力せよ．

1
A
4
A A B B
5
L M N L N
6
K K K K K K
6
X X X Y Z X
10
A A A B A C A C C B
10
U U U U U V V W W W
0

A 1
TIE
TIE
K 4
X 5
A 7
U 8

竹の寿命は数十年あり，一生の最後に花を咲かせて種をつくる． 筑波を旅行していた生物学者の ACM 博士は偶然見かけた竹の花の美しさに魅了され， 竹の花を毎年見られる庭を作りたいと思った． ACM 博士は，竹の品種改良をはじめて，ついに竹の寿命を操作した品種を作る方法を確立した． この方法を使えば，任意の年数で花を咲かせる竹の品種を作ることができる．

種をまいてから k 年で花を咲かせる竹を k 年竹と呼ぶことにしよう． k 年竹は種をまいてから k 年で種を作って枯れる． したがって，さらに k 年後には次の世代が花を咲かせる． このように，k 年竹の種をまくと，k 年周期で花が見られる． 例えば， 15 年竹の種をまくと， 15 年後，30 年後，45 年後というように 15 年ごとに花が見られる．

あなたは，ACM 博士に庭の設計を依頼された．庭はいくつかの区画に区切られている． 1 つの区画では同じ品種の竹しか育てることができない． ACM 博士の依頼は，できるだけ多くの年にどこかの区画で竹の花を見るには， 各区画にどの品種の竹の種をまけばよいかを決めて欲しいというものである．

あなたは，すぐに全ての区画に1年竹の種をまくことを提案した． しかし，ACM 博士によれば寿命の短い竹の品種は作るのが難しいので， 寿命が長い竹だけしか使わない庭を設計して欲しいそうだ． 最初の竹が咲くまで待つのはかまわないが， その後は毎年花が見られるようにして欲しいということだ． 今度は，例えば 10 年竹を使って，今年はある区画に，来年は別区画にというように， 10 年間異なる区画にまき続けることを提案した．そうすれば， 10 年後以降毎年どこかの区画で花が見られる．しかし ACM 博士は， もう全区画に今年種をまくと決めたのだ，と反対した．

そこであなたは，

• m 年以上の寿命の竹だけを使い，
• すべての区画に今年種をまく

という条件で，m 年後以降できるだけ長い期間どこかの区画では花が咲くような種のまき方を考えることにした．

入力は最大で 50 個のデータセットからなる． 各データセットは次の形式で表される．

m n

整数 m (2 ≤ m ≤ 100) は造園に使える最短の寿命の竹の寿命（年）である． 整数 n (1 ≤ n ≤ 500,000) は区画の数である．

入力の終わりは 2 つのゼロからなる行で表される．

いくらよい計画を作っても，どの区画でも花が咲かない「退屈な年」がいつか必ずやってくる． 各データセットについて， m 年目以降で初めて訪れる退屈な年が今から何年後かを示す整数だけからなる行を出力せよ．

なお， m = 2, n = 500,000 （Sample Input の最後のデータセット）のとき答が最大となる．

3 1
3 4
10 20
100 50
2 500000
0 0

4
11
47
150
7368791

あなたは，「ダルマ落とし」と呼ばれるゲームの一種を遊んでいる．

ゲームの開始時には，様々な重さの同じ大きさの木のブロックがいくつか，塔状に積んである． その上にはダルマを表すブロックがある． あなたは木槌を持っているが，その頭はブロック一つの高さよりより太く，二つ分よりは細い．

あなたは，一番上のダルマ以外の隣り合うブロック二つで重さの差が 1 以下の対のどれかを選び， 木槌の一撃で両方叩き出すことができる． その上にあったブロックは塔を崩さず真下に落ちる． 重さの差が 2 以上の対は，塔のバランスを保ったまま木槌を振り抜くのが難しいため，叩き出せない． 三つのブロックを同時に叩き出すのには超人的精度を要するので，到底無理だ．

ゲームの目標はできるだけ多くのブロックを取り除くことである． あなたの仕事は，最適な叩き出しの順序を選んだときに， 取り除けるブロックの個数を求めることである．

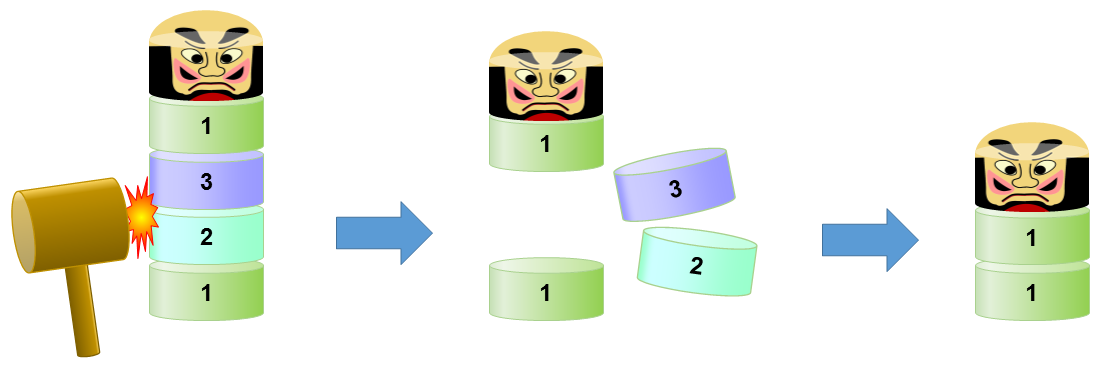
図D1. 二つのブロックを同時に叩き出す

上図のように，重さ 1, 2, 3, 1 の 4 ブロックが下からこの順で積んであるとき， 重さ 2 と 3 の中央のブロック二つを一度に叩き出すことができる． 上のブロックは下に落ちて，残るのは重さ 1 のブロック二つとダルマブロックになる． 残った重さ 1 のブロックの対は，さらに続けて叩き出すことができる．

入力は複数のデータセットからなる． データセットの数は 50 以下である． 各データセットは次の形式で表される．

n
w₁ w₂ … w_n

n は一番上のダルマを除くブロックの個数を表す． n は，正の整数であり，300 を超えない． w_i は下から i 番目のブロックの重さを表す． w_i は整数であり，1 以上，1000 以下である．

入力の終わりは，1 個のゼロだけからなる行で表される．

各データセットについて，取り除くことができるブロックの最大個数を 1 行に出力せよ．

4
1 2 3 4
4
1 2 3 1
5
5 1 2 3 6
14
8 7 1 4 3 5 4 1 6 8 10 4 6 5
5
1 3 5 1 3
0

4
4
2
12
0

立方体印刷によるインスタレーションコンテスト (Installation art Contest with Printed Cubes, ICPC) に出品するため， 我々は 3D プリンタを使って立方体を組み合わせたインスタレーションの作品をデザインしている． 今回はちょうど k 個の同じ大きさで同じ向きの立方体を用いて作品を作ることを試みている．

まず， CAD を用いて，立方体を配置する場所の候補となる場所を n (n ≥ k) 個 3D 空間中に用意する． 立方体を全ての候補場所に置いたとすると， 以下の 3 条件が満たされる．

• 各立方体は 0 個，1 個 または 2 個の立方体と重なることがあるが，3 個以上とは重ならない．
• ある立方体が 2 個の立方体と重なるとき，その 2 個の立方体は重ならない．
• 面や辺や頂点で接触するだけで重なりのない 2 個の立方体はない．

つぎに，この n 個の候補の中から k 個の異なる場所を上手に選び， そこに立方体を配置して， k 個の立方体の併合としてひとつの連結した多面体を得る． 3Dプリンタを用いるときは， 物体の薄い表面だけを印刷するのが普通である． プリンタ用の材料を節約するため， 最小の表面積を持つ多面体を見つけたい．

あなたの仕事は， 与えられた n 個の位置の中から選ばれた k 個の位置に置かれた k 個の連結する立方体が作る多面体のうち表面積が一番小さいものを探すことである．

図 E1. 連結した同じ大きさの立方体からなる多面体．

入力は複数のデータセットからなる． データセットの数は 100 以下である． 各データセットは次の形式で表される．

n k s
x₁ y₁ z₁
...
x_n y_n z_n

1 行目の n は準備された場所の総数， k は求める多面体を構成する連結した立方体の個数， s は立方体の 1 辺の長さである． n, k, s はすべて整数であり．空白文字で区切られる． 続く n 行は立方体を配置しうる場所の座標を指定する． その i 行目には x_i, y_i, z_i の 3 個の整数があり， これらは立方体の頂点の中で座標値が最小のものを配置しうる座標を表す． 立方体の辺は座標軸のどれかと平行である． 座標値はすべて整数であり， 空白文字で区切られる． 配置場所に関する上述の 3 条件は満たされている．

各パラメタは以下の条件を満たす: 1 ≤ k ≤ n ≤ 2000, 3 ≤ s ≤ 100, -4×10⁷ ≤ x_i, y_i, z_i ≤ 4×10⁷.

入力の終わりは，空白で区切られた 3 個のゼロからなる行で表される．

各データセットについて， 表面積最小の連結した多面体の表面積を表す整数を 1 行に出力せよ． 連結した多面体を構成する k 個の立方体がない場合は -1 を出力せよ．

1 1 100
100 100 100
6 4 10
100 100 100
106 102 102
112 110 104
104 116 102
100 114 104
92 107 100
10 4 10
-100 101 100
-108 102 120
-116 103 100
-124 100 100
-132 99 100
-92 98 100
-84 100 140
-76 103 100
-68 102 100
-60 101 100
10 4 10
100 100 100
108 101 100
116 102 100
124 100 100
132 102 100
200 100 103
192 100 102
184 100 101
176 100 100
168 100 103
4 4 10
100 100 100
108 94 100
116 100 100
108 106 100
23 6 10
100 100 100
96 109 100
100 118 100
109 126 100
118 126 100
127 118 98
127 109 104
127 100 97
118 91 102
109 91 100
111 102 100
111 102 109
111 102 118
111 102 91
111 102 82
111 114 96
111 114 105
102 114 114
93 114 114
84 114 105
84 114 96
93 114 87
102 114 87
10 3 10
100 100 100
116 116 102
132 132 104
148 148 106
164 164 108
108 108 108
124 124 106
140 140 104
156 156 102
172 172 100
0 0 0

60000
1856
-1
1632
1856
2796
1640

謎の組織が残した画像データが発見された．あなたは，この画像データを解析することを依頼された．その組織では独自の文字が用いられていて，それぞれの文字は白い紙に黒インクで記したものが，2 値画像として表されている．

それぞれの文字を表現する画像には多くのバリエーションが存在するが，ふたつの画像が同じ文字を表すかどうかは連結成分の包含関係で判定できることがわかった．ここでは以下の用語を定義する．なお，画像の範囲外は白のピクセルで埋まっているものと考える．

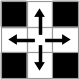
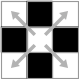
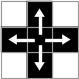
• 白の連結成分 : 縦横につながっている白ピクセルからなる集合． (下図)
• 黒の連結成分 : 縦横斜めにつながっている黒ピクセルからなる集合． (下図)
• 連結成分 : 白または黒の連結成分．
• 背景連結成分 : 画像範囲外のピクセルを含む連結成分．画像の最外側の白ピクセルは背景連結成分の一部になる．

連結	非連結	連結	連結
白の連結性		黒の連結性

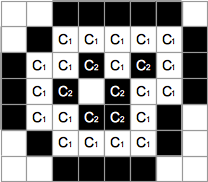
C₁ をある画像のひとつの連結成分，C₂ を同じ画像の反対色の連結成分とする．ここで C₁, C₂ 以外のピクセルを，すべて C₂ の色に変えた画像を考える．C₁ と C₂ が共に背景連結成分でないならば，背景連結成分の色もC₂ の色に変える．そのように変更した画像でも C₂ のピクセルが背景連結成分に含まれないとき，元の画像について C₁ は C₂ を包含するという．(下図)

ふたつの画像は以下の両条件が満たされるとき同じ文字を表す．

• 両画像は同数の連結成分を持つ．
• ふたつの画像に含まれる連結成分の集合をそれぞれ S, S' とすると，以下の両条件を満たす全単射 f : S → S' が存在する．
• S のすべての要素 C について，C の色と f (C) の色は同じである．
• S のすべての要素 C₁, C₂ について，C₁ が C₂ を包含することが f (C₁) が f (C₂) を包含することの必要十分条件である．

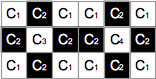
例を示す．下図の画像中の連結成分は以下の包含関係を持つ．

• C₁ が C₂ を包含する．
• C₂ が C₃ を包含する．
• C₂ が C₄ を包含する．
• C'₁ が C'₂ を包含する．
• C'₂ が C'₃ を包含する．
• C'₂ が C'₄ を包含する．

これらの各連結成分について，f (C_i) = C'_iで定義される全単射は上述の条件を満たしている．したがって，左の画像と右の画像は同じ文字を表していることが分かる．

与えられた ふたつの画像が同じ文字を表すかどうかを判定するプログラムを作成しなさい．

入力は最大で 200 個のデータセットからなる．入力の終わりはゼロふたつからなる行である．各データセットは次の形式をしている．

画像 1
画像 2

各画像は以下の形式をしている．

h w
p_(1,1) ... p_(1,w)
...
p_(h,1) ... p_(h,w)

h と w は画像の高さと幅のピクセル数であり，1 ≤ h ≤ 100, 1 ≤ w ≤ 100 と仮定して良い．続く h 行はそれぞれ w 個の文字からなる．p_(y,x) は，左上隅から数えて上から y 番目，左から x 番目のピクセルの色を表す文字である．文字は白を表すピリオド (".") と黒を表すシャープ ("#") のいずれかである．

入力データセットごとに，ふたつの画像が同じ文字を表すときには "yes", さもなければ "no" をそれぞれ 1 行に出力しなさい．出力には余分な文字を含んではならない．

3 6
.#..#.
#.##.#
.#..#.
8 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#..#..#
.#####.
...#...
3 3
#..
...
#..
3 3
#..
.#.
#..
3 3
...
...
...
3 3
...
.#.
...
3 3
.#.
#.#
.#.
3 3
.#.
###
.#.
7 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#.....#
.#####.
7 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#..#..#
.#####.
7 7
.#####.
#.....#
#..#..#
#.#.#.#
#..#..#
#.....#
.#####.
7 11
.#####.....
#.....#....
#..#..#..#.
#.#.#.#.#.#
#..#..#..#.
#.....#....
.#####.....
7 3
.#.
#.#
.#.
#.#
.#.
#.#
.#.
7 7
.#####.
#..#..#
#..#..#
#.#.#.#
#..#..#
#..#..#
.#####.
3 1
#
#
.
1 2
#.
0 0

yes
no
no
no
no
no
yes
yes

飛行時間を大幅に短縮するワープ航法は空の旅を変革しつつある．航空機は，地表面に設置したワープ場の上に到達しさえすれば，好きな行き先に瞬く間に移動できるのだ．

残念ながらこの分野の現在の未熟な技術ではワープ場の設置はとても高価につく． 予算が許す範囲では 2 箇所にしか設けられない． 幸いにしてワープ場のコストは設置場所に依存しないので，地表面のどこにでもワープ場を設置してもよい．空港に設置することさえできる．

あなたの仕事は，空港の位置とその間の片道航空便の一覧をもとに，平均コストを最小にできる 2 箇所のワープ場の設置場所をみつけることだ． 平均コストとは，全航空便の飛行時間の二乗平均平方根，すなわち以下で与えられる．

ここで，m は航空便の総数，t_j は j 番目の便の最短飛行時間である． t_j の値はワープ場の設置場所に依存することに注意せよ．

簡単のため，地表面は平坦な二次元平面で，空港，航空機，ワープ場はその平面上の点で近似するものとする． 航空便が使う航空機の巡航速度は異なり得る． 航空機の上昇，加速，減速，降下に要する時間は無視できる． また，ワープ場に到達した航空機がそこから行き先に移動するのに掛かる時間はゼロである． 後述するように，空港の座標はすべて整数で与えられるが，ワープ場の座標は非整数値を取りうることに注意せよ．

入力は 35 個以下のデータセットからなる．各データセットは次の形式で表される．

n m
x₁ y₁
...
x_n y_n
a₁ b₁ v₁
...
a_m b_m v_m

n は空港の数，m は航空便の数を表す(2 ≤ n ≤ 20, 2 ≤ m ≤ 40)． 各 i について，(x_i, y_i) は i 番目の空港の座標を表す． それぞれの座標値 x_i, y_i は整数であり，その絶対値は 1000 を超えない． 各 j について，a_j と b_j は 1 から n までの整数で，それぞれ j 番目の航空便の出発空港と到着空港の番号を表す． また，v_j は j 番目の航空便の航空機の巡航速度，すなわち単位時間あたりの移動距離を表す． v_j は十進小数であり，小数第二位まで与えられる (1 ≤ v_j ≤ 10)．

以下のことが保証されている．

• 異なる空港は異なる座標を持つ．
• すべての航空便で，出発空港と到着空港は異なる．
• 異なる航空便は出発空港と到着空港の少なくとも一方が異なる．

入力の終わりは，2つのゼロからなる行で表される．

各データセットについて，2 箇所のワープ場を最適に設置した場合の平均コストを出力せよ．出力には 10^-6 を超える絶対誤差があってはならない．

3 4
100 4
100 0
0 0
1 2 1.00
2 1 1.00
3 1 9.99
3 2 9.99
7 6
0 0
1 0
2 0
0 10
1 10
2 10
20 5
1 7 1.00
2 7 1.00
3 7 1.00
4 7 1.00
5 7 1.00
6 7 1.00
4 4
-1 -1
1 -1
-1 1
1 1
1 4 1.10
4 2 2.10
2 3 3.10
3 1 4.10
8 12
-91 0
-62 0
-18 0
2 0
23 0
55 0
63 0
80 0
2 7 3.96
3 2 2.25
2 4 5.48
8 7 9.74
5 6 6.70
7 6 1.51
4 1 7.41
5 8 1.11
6 3 2.98
3 4 2.75
1 8 5.89
4 5 5.37
0 0

1.414214
0.816497
0.356001
5.854704

TKB市のある学校において，生徒同士のプレゼント交換会を行うことになった．

このパーティでは，親しい関係にある生徒のペアで，必ず 1 つのプレゼントが一人の生徒からもう一人の生徒へと渡され，逆向きはない． プレゼントの方向，すなわちペアのどちらがプレゼントをもらうかはあらかじめ決めておく． この他のプレゼントの交換はない．

それぞれのペアがプレゼントの方向をランダムに決めたら， 数えきれないプレゼントをもらう生徒がいる一方で，ほんの少ししか，あるいはまったくもらえない生徒も出てくるかもしれない．

あなたは親しい友達のペアすべてについてプレゼントの向きを決めて， ひとりの生徒がもらえるプレゼントの最小数と最大数の差をできるだけ小さくしたい． 差を最小にしたときにもらえるプレゼントの最小数と最大数を求めよ． 差が最小となるやり方が複数ある場合は，最小の受け取り数が最大となるものを求めよ．

入力は高々 10 個のデータセットからなる． 各データセットは次の形式で表される．

n m
u₁ v₁
...
u_m v_m

n は生徒の人数，m は友人関係の数を表す (2 ≤ n ≤ 100, 1 ≤ m ≤ n (n-1)/2). 生徒は 1 から n までの整数で表される． 続く m 行は友人関係を表している：各 i について生徒 u_i と v_i が友人であることを意味する (u_i < v_i)． 同じ友人関係が複数回記述されることはない．

入力の終わりは，2つのゼロからなる行で表される．

各データセットについて，空白で区切られた 2 つの整数 l, h からなる行を出力せよ． ここで l はもらえるプレゼントが最も少ない生徒のプレゼント数，h はもらえるプレゼントが最も多い生徒のプレゼント数である．

3 3
1 2
2 3
1 3
4 3
1 2
1 3
1 4
4 6
1 2
1 3
1 4
2 3
3 4
2 4
0 0

1 1
0 1
1 2