平面上に面積が等しい二つの三角形 T₁ と T₂ がある．三角形 T₁ に以下の操作を繰り返して，T₁ が T₂ とちょうど重なるようにしたい．このとき T₁ のどの頂点を T₂ のどの頂点と重ねても構わない．T₁ を T₂ と重ねるのに最小で何回の操作が必要か計算せよ．

(操作): 三角形のうちどれか 1 頂点を選び，それを通る対辺に平行な直線上の任意の点に動かす．

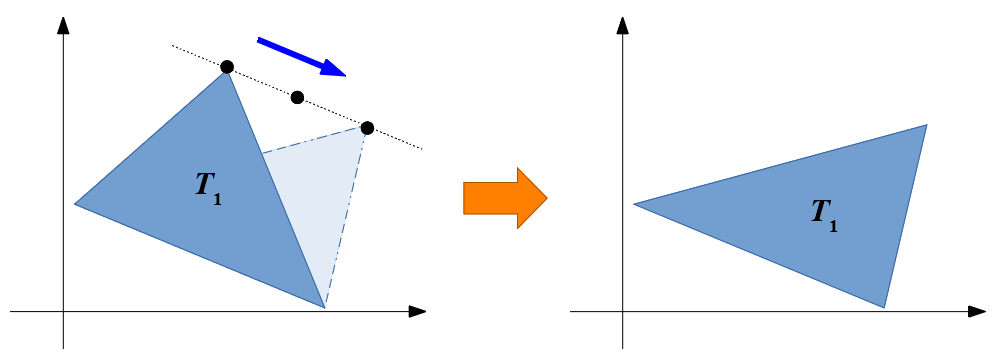
操作の例

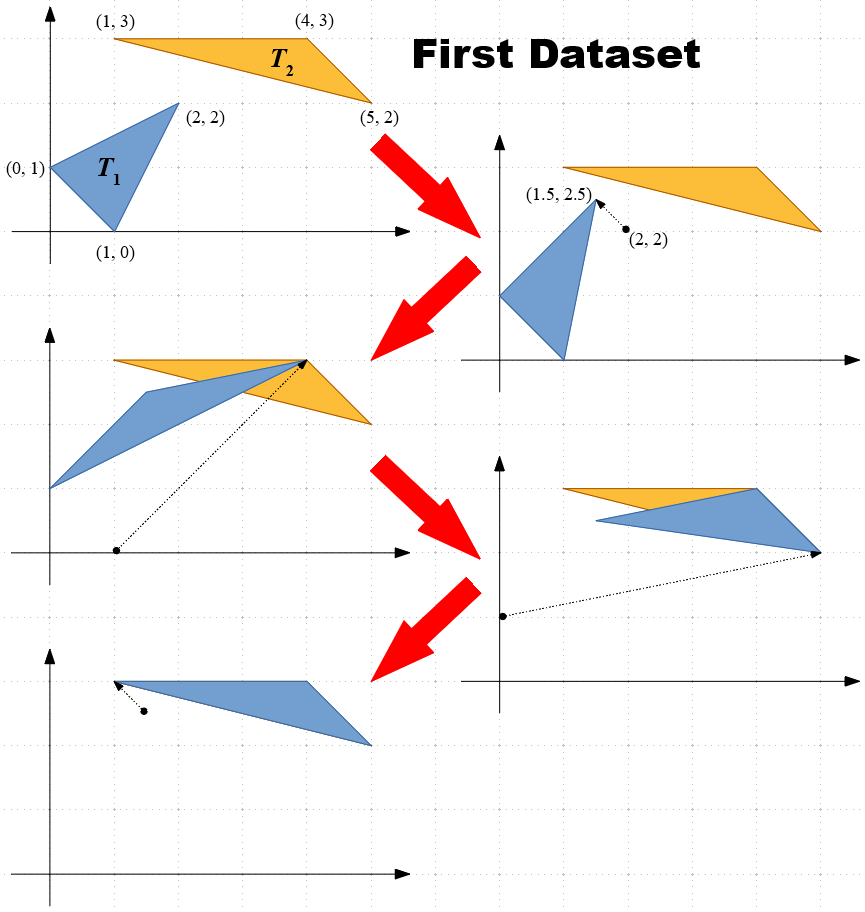
下図に Sample Input の最初のデータセットに対してありうる操作列を示す．

入力は 2000 個以下のデータセットからなる．各データセットは次の形式で表される．

x₁₁ y₁₁
x₁₂ y₁₂
x₁₃ y₁₃
x₂₁ y₂₁
x₂₂ y₂₂
x₂₃ y₂₃

(x_ij, y_ij) は T_i の j 番目の頂点の座標を表す．

以下のことが保証される．

• 座標はすべて整数で，絶対値は 1000 以下である．
• T₁ と T₂ は等しい正の面積を持つ．
• 与えられる 6 つの頂点はすべて相異なる．

データセットの間には空行が 1 つある．

入力の終わりはEOFで表される．

各データセットについて，必要な最小の操作回数を 1 行に出力せよ．5 回以上の操作が必要である場合は Many と出力せよ．

移動した頂点の座標値は整数値とは限らないことに注意せよ．

なお，上記の制約を満たす任意の入力に対して，必要な操作回数はある定数以下であることを証明できる．

0 1
2 2
1 0
1 3
5 2
4 3

0 0
0 1
1 0
0 3
0 2
1 -1

-5 -4
0 1
0 15
-10 14
-5 10
0 -8

-110 221
-731 525
-555 -258
511 -83
-1000 -737
66 -562

533 -45
-525 -450
-282 -667
-439 823
-196 606
-768 -233

0 0
0 1
1 0
99 1
100 1
55 2

354 -289
89 -79
256 -166
131 -196
-774 -809
-519 -623

-990 688
-38 601
-360 712
384 759
-241 140
-59 196

629 -591
360 -847
936 -265
109 -990
-456 -913
-787 -884

-1000 -1000
-999 -999
-1000 -998
1000 1000
999 999
1000 998

-386 -83
404 -83
-408 -117
-162 -348
128 -88
296 -30

-521 -245
-613 -250
797 451
-642 239
646 309
-907 180

-909 -544
-394 10
-296 260
-833 268
-875 882
-907 -423

4
3
3
3
3
4
4
4
4
Many
Many
Many
Many