Links
Problem A
太郎君の買物
お母さんは太郎に初めてのお買物経験をさせてみることにした. お母さんは商品カタログから好きなものを二つ選んでいいのよと言うのだが,欲しいものばかりなので太郎は決められなくて困った. そこで,お母さんが許してくれる金額の範囲で, 合わせた値段が一番高くなる二つの品物を買うことにした. 同じものが二つあってもつまらないから,別々の二つが欲しい.
太郎が二つの品物を選ぶのを助けてほしい. 全商品の価格表が与えられる. この中の品物二つの組のうち,価格の合計が許容額の範囲で最も高いものを見つけ,その価格の合計を答えよ. 太郎が買う品物の数は二つに決まっていて,一つでも,三つ以上でもいけない. 二つ以上の品物が同じ価格のこともあることに注意せよ.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n m
a1 a2 … an
データセットは 2 行からなる. 1 行目には品物の個数 n と使ってよい最大の金額 m が与えられる. n は整数であり,2 ≤ n ≤ 1000 が成り立つ. m は整数であり,2 ≤ m ≤ 2,000,000 が成り立つ. 2 行目には n 個の品物の価格が与えられる. ai (1 ≤ i ≤ n) が i 番目の品物の価格である. この値は整数であり,1 以上 1,000,000 以下である.
入力の終わりは,2 個のゼロだけからなる行で表される. 全データセットの n の合計は 50,000 を超えない.
Output
各データセットについて,品物二つの組のうち価格の合計が許容額 m を超えない範囲で最も高いものを見つけ,その価格の合計を 1 行に出力せよ. どの品物の組も価格合計が m を超える場合は,代わりに NONE と出力すること.
Sample Input
3 45 10 20 30 6 10 1 2 5 8 9 11 7 100 11 34 83 47 59 29 70 4 100 80 70 60 50 4 20 10 5 10 16 0 0
Output for the Sample Input
40 10 99 NONE 20
Problem B
ほとんど同じプログラム
Concours de Programmation Comtemporaine Interuniversitaire (CPCI) というプログラミングコンテストは, ICPC と似た方法で審判する. 二つの異なる入力に対する正しい解答を提出しなければ,正答として受理されない. 提出それぞれには解答を生成したプログラムを添付する. 二つの提出が正しい解答と認められるには,両者の出力が正しいことに加え, 添付したプログラムが完全に同じものでなくてはならない.
ところが,2 回の提出で異なる入力を処理しようとして, 入力ファイル名を表す文字列定数一つだけを変更したプログラムを 2 回目に提出してしまう参加者が後を絶たない. このような惜しい提出に対しては, 特別なエラーメッセージを表示して, 参加者に問題点を伝わりやすくするのがよいかもしれないと CPCI の主催者は考えている. このような惜しい提出を検出するのがあなたの仕事である.
Input
入力は高々 100 個のデータセットからなる. 各データセットは次の形式で表される.
s1
s2
s1 と s2 はそれぞれ 1 行に書かれた長さ 1 以上 200 以下の文字列であり, 1 番目と 2 番目の提出プログラムを表している. プログラムは,英小文字 (a, b, ..., z),英大文字 (A, B, ..., Z),数字 (0, 1, ..., 9),二重引用符 ("),およびセミコロン (;) からなり,二重引用符が含まれる場合は,必ず偶数個含まれる.
入力の終わりは ‘.’(ピリオド)一つのみからなる行で表される.
Output
各データセットについて,判定結果を 1 行に出力せよ.
与えられた二つのプログラムが完全に等しければ IDENTICAL と出力せよ. 二つのプログラム中の対応する文字列定数一つだけが異なるならば CLOSE と出力せよ. それ以外の場合,DIFFERENT と出力せよ. 文字列定数とは,奇数番目の二重引用符とその次の二重引用符の間の(空でありうる)文字の並びである.
Sample Input
print"hello";print123 print"hello";print123 read"B1input";solve;output; read"B2";solve;output; read"C1";solve;output"C1ans"; read"C2";solve;output"C2ans"; """""""" """42""""" slow"program" fast"code" "super"fast"program" "super"faster"program" X"" X I"S""CREAM" I"CE""CREAM" 11"22"11 1"33"111 .
Output for the Sample Input
IDENTICAL CLOSE DIFFERENT CLOSE DIFFERENT DIFFERENT DIFFERENT CLOSE DIFFERENT
Problem C
池のある庭園
モダンな庭園の設計者であるガーディナー氏は,自然の地形を活かすことにとても長けている. その設計法はユニークで,最初にまず池の位置を決め,自然の地形に手を加えずに池を設計する.
彼独特の手順で設計すると池の形は必ず簡単な縦横比の長方形になる. ガーディナー氏はまず,庭の用地の地図上に単位正方形のセルに分割する格子を描き,各セルに標高を記す. 彼の設計法では,池はいくつかのセルからなる長方形領域を占める. 領域の一番外側の各セルは,内部のどのセルよりも高くなくてはならない. たとえば,以下のグリッド状の地図(数値は標高を表す)では,灰色の領域(濃い灰色が一番外側のセル,薄い灰色が内部のセルを表す)に池を作ることができる. 一番外側のセルは最低でも高さが 3 あり,内部のセルは最高でも高さが 2 であることは,容易に見て取れるであろう.
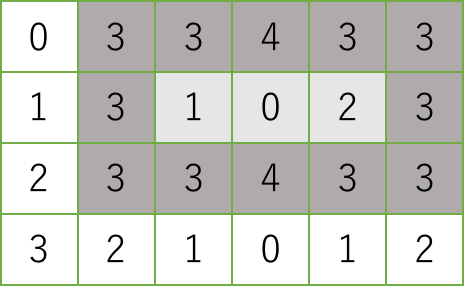
池を作る長方形領域は,内部セルを少なくとも一つ持つ必要がある. したがって,幅も奥行きも 3 以上でなければならない.
池の内部セルに水を注ぐと,水位が一番外側のセルの中で最も低いところに達するまで水を溜めることができる. さらに注ぎ続ければ,水は当然溢れ出てしまう. ガーディナー氏は,池の容量は大きければ大きいほど良いと考えている. ここで,池の容量とは,溜められる水の最大量のことである. たとえば,上の地図で灰色の領域に池を作った場合,池の容量は (3 − 1) + (3 − 0) + (3 − 2) = 6 になる. ここで,3 は一番外側のセルの中で最も低いものの標高であり,1, 0, 2 は内部セルの標高である. 単位正方形の各セルの標高が記されたグリッド状の地図を与えられた時,この用地に作れる池の最大容量を計算するプログラムを作成するのが,あなたの仕事である.
なお,以下のどちらの長方形領域も池にはならない. 左側の場合,右下隅のセルが内部セルより高くない. 右側の場合,真ん中のセルが一番外側のセルと同じ高さである.
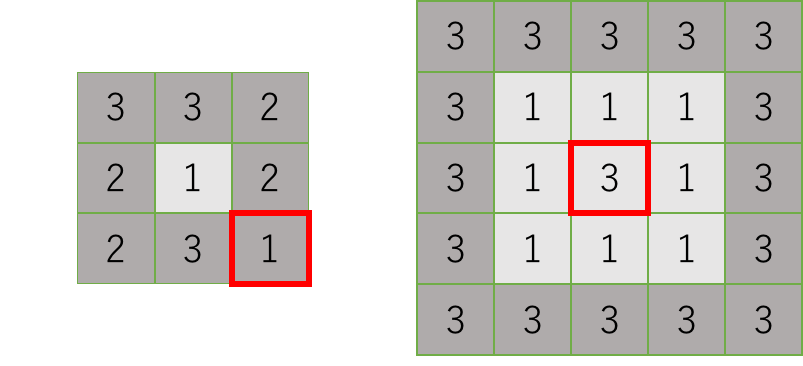
Input
入力は高々 100 個のデータセットからなる. 各データセットは次の形式で表される.
d w
e1, 1 ... e1, w
...
ed, 1 ... ed, w
最初の行の d と w はそれぞれ地図に示す庭の用地の奥行きと幅を表しており,3 以上 10 以下の整数である. 続く d 行では,各行が空白文字 1 個で区切られた w 個の 0 以上 9 以下の整数を含んでいる. この d 行中 y 番目の行の x 番目の整数は,座標 (x, y) の単位正方形のセルの標高である.
入力の終わりは,空白文字 1 個で区切られたゼロ 2 個からなる行で表される.
Output
各データセットに対し,そのデータセットが示す庭の用地に作れる池のうち,最大容量のものの容量を 1 行に出力せよ. もし,池が作れない場合にはゼロを 1 行に出力せよ.
Sample Input
3 3 2 3 2 2 1 2 2 3 1 3 5 3 3 4 3 3 3 1 0 2 3 3 3 4 3 2 7 7 1 1 1 1 1 0 0 1 0 0 0 1 0 0 1 0 1 1 1 1 1 1 0 1 0 1 0 1 1 1 1 1 1 0 1 0 0 1 0 0 0 1 0 0 1 1 1 1 1 6 6 1 1 1 1 2 2 1 0 0 2 0 2 1 0 0 2 0 2 3 3 3 9 9 9 3 0 0 9 0 9 3 3 3 9 9 9 0 0
Output for the Sample Input
0 3 1 9
Problem D
弁当作り
太郎君は,近頃弁当作りにはまっている. 太郎君は今日新しい弁当レシピ本を手に入れたので,そこに書いてあるレシピをできるだけ多く試してみたいと思っている.
どのレシピに必要な材料も十分に手元にあるのだが,みんな 2 つ入りの真空パックになっている. 1 つだけ使って 1 つ残したら,残った方はすぐ腐ってしまう. かといって同じレシピの弁当を 2 つ作っても面白くない. だから彼は同じ弁当を複数作らず,しかも半端な材料が残らないようなレシピの組み合わせを選ぶことにした.
レシピ本には,同じ材料を使っても違うレシピの弁当も載っているかもしれないことに注意せよ.
この方針に従うと,今日太郎君は最大で何種類のレシピを試せるのだろうか.
Input
入力は 50 個以下のデータセットからなる. 各データセットは次の形式で表される.
n m
b1,1...b1,m
...
bn,1...bn,m
1 行目には,レシピ本に書いてあるレシピの数 n と材料の種類数 m が与えられる. n と m は整数であり,1 ≤ n ≤ 500,1 ≤ m ≤ 500,1 ≤ n × m ≤ 500 が成り立つ. 続く n 行には,0 または 1 からなる長さ m の文字列で各レシピの情報が与えられる. bi,j は i 番目のレシピに j 番目の材料が必要かどうかを表し,0 の場合は必要ないこと,1 の場合は必要であることを意味する. 各行は少なくとも 1 つ以上の 1 を含む.
入力の終わりは,2 つのゼロからなる行で表される.
Output
各データセットについて,太郎君が試すことのできるレシピの種類の最大数を 1 行に出力せよ.
Sample Input
4 3 110 101 011 110 7 1 1 1 1 1 1 1 1 4 5 10000 01000 00100 00010 6 6 111111 011000 100000 000010 100001 100100 0 0
Output for the Sample Input
3 6 0 6
Problem E
論理式圧縮機
あなたは論理式の意味を保ったまま短くする圧縮機の作成を依頼された.
論理式の文法は, 0 1 a b c d - ^ * ( ) を終端記号,<E> を開始記号とし,次の生成規則を持つ.
<E> ::= 0 | 1 | a | b | c | d | -<E> | (<E>^<E>) | (<E>*<E>)
ここで,a, b, c, d は, 値として 0 または 1 を持つ論理変数である. 各演算子は下の表に示すように評価する. すなわち,- は否定 (NOT) を, ^ は排他的論理和 (XOR) を, * は論理積 (AND) をそれぞれ表す.
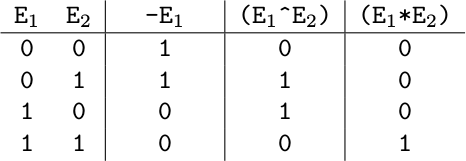
4 変数がどんな値を持っていても与えられた式と同じ評価結果になる式のうちで, 最も短い式の長さを求めるプログラムを書きなさい.
例えば,Sample Input の最初にある式 0 は, これ以上短くすることができない.したがって,最短の長さは 1 である.
Sample Input の 2 番目の (a*(1*b)) は, (a*b) や (b*a) と必ず同じ計算結果になり, これらが最短である.したがって,出力は 5 になる.
Input
入力は複数のデータセットからなる. データセットは 1 行であり,上述の文法に従う式一つが書かれている. 式の長さは 16 文字以下である.
入力の終わりは ‘.’ (ピリオド) 一つのみからなる行で表される. 入力に含まれるデータセットの数は高々 200 である.
Output
各データセットについて, 変数の値の全組み合わせに対して,同じ値を計算する最も短い式の長さを表す整数一つからなる行を出力せよ.
Sample Input
0 (a*(1*b)) (1^a) (-(-a*-b)*a) (a^(b^(c^d))) .
Output for the Sample Input
1 5 2 1 13
Problem F
リボンたたみ
薄くてとても長いリボンを何度も折りたたむとする. まずリボンを左右に伸ばし,中央に折り目をつけて,片方の半分をもう一方の上に重ねる. リボンの左端を持ち上げて右端に重ねるという左から右への折り方でも, 逆に右から左への折り方でも良い. 折ったリボンをさらに折りたたむときは, 折り重なったリボン全体を 1 枚として扱う. 折り方はやはり左から右でも逆でも良い.
この折りたたみを何度か繰り返した後,何枚も重なっているリボンのうちの 1 枚に印をつけてから, リボンを元の状態にまで完全に広げ直す. 広げたリボンにはたくさん折り目が付いているわけだが, 折り目と折り目,あるいは折り目と端の間の部分のひとつに印がついているはずだ. 上から何枚目に印をつけたのかと,リボンを広げたとき印をつけた部分がどこにあるのかわかれば, 繰り返した折りたたみがそれぞれ左右のどちらからだったのかわかるかな.
下図は Sample Input の最初のデータセットの場合を示すものである.
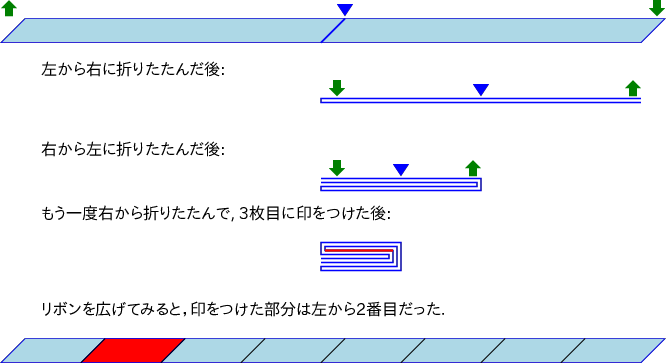
Input
入力は最大 100 データセットからなり,その各々は 1 行にみっつの整数が並んだものである.
n i j
みっつの整数は,ある折りたたみ順で n 回折りたたんでから, 上から i 枚目に印をつけ, リボンを元の状態にまで完全に広げ直したら, 印をつけたのは折り目で区切られた左から j 番目の部分だった, という意味である. i, j はどちらも 1 から数え始める. つまり,重なりの一番上は 1 枚目,左端の部分は 1 番目である. みっつの整数は,1 ≤ n ≤ 60, 1 ≤ i ≤ 2n, 1 ≤ j ≤ 2n を満たす.
入力の終わりはゼロ 3 個の行で示す.
Output
各データセットについて,データセットに示す結果になる折りたたみ列のひとつを出力せよ.
折りたたみ列は文字 L または文字 R を n 個並べた 1 行で表す. L は左から右,R は右から左への折りたたみを表し,操作列中の順に折りたたむものとする.
Sample Input
3 3 2 12 578 2214 59 471605241352156968 431565444592236940 0 0 0
Output for the Sample Input
LRR RLLLRRRLRRLL LRRRLRRLLRRRRLLLLRLLRRRLRRLLRLLLLLLRLRLLRLRLLLRLRLLRLLRRRLL
Problem G
迷宮を一周
探検家の太郎君は迷宮の平面図を手に入れた. この迷宮は二次元グリッド状で,平面図上の各マスは部屋に対応しており,各部屋に入れるかどうかは平面図に記されている. 北西の角,平面図上で左上の部屋にはこの迷宮の唯一の出入り口があり,残りの南西,南東,北東の 3 つの角の部屋にはそれぞれ宝箱が置かれている. 宝箱を手に入れるためには,宝箱の置かれている角の部屋まで移動しなければならない.
太郎君は出入り口のある部屋からスタートし,東西南北の四方向に隣接する入れる部屋への移動を繰り返し,最終的に 3 つの宝箱を全て回収して再び出入り口のある部屋に戻って来たい. 困ったことに,この迷宮は相当に荒れ果てていて,出入り口のある部屋以外は,たとえ入れる部屋でも床がとても壊れやすく,一度通ると崩れ落ちて,その部屋には二度と入れなくなってしまう. 全ての宝箱を回収して出入り口のある部屋に戻ることが可能か判定せよ.
Input
入力は 100 個以下のデータセットからなる. 各データセットは次の形式で表される.
N M
c1,1...c1,M
...
cN,1...cN,M
1 行目には,南北方向の部屋の数 N と東西方向の部屋の数 M が与えられる. N と M は整数であり, 2 ≤ N ≤ 50, 2 ≤ M ≤ 50 が成り立つ. 続く N 行には長さ M の文字列が与えられる. i 行,j 列の文字 ci,j は,北端から i 番目,西端から j 番目の部屋 (i,j) の状態を表しており,入れる部屋であることを表すピリオド ('.') と入れない部屋であることを表すナンバーサイン ('#') のいずれかである. 迷宮の出入り口があるのは部屋 (1,1) であり,宝箱は (N,1),(N,M),(1,M) の 3 つの部屋に置かれている.これら 4 つの部屋は全て入ることができる. 与えられた N × M 室の部屋の外に出ることはできない.
入力の終わりは,2 つのゼロからなる行で表される.
Output
各データセットについて,全ての宝箱を回収して出入り口のある部屋に戻ることが可能な場合は YES,不可能な場合は NO をそれぞれ 1 行に出力せよ.
Sample Input
3 3 ... .#. ... 5 5 ..#.. ..... #.... ..... ..... 3 8 ..#..... ........ .....#.. 3 5 ..#.. ..... ..#.. 4 4 .... .... ..## ..#. 0 0
Output for the Sample Input
YES NO YES NO NO
Problem H
等積変形
平面上に面積が等しい二つの三角形 T1 と T2 がある.三角形 T1 に以下の操作を繰り返して,T1 が T2 とちょうど重なるようにしたい.このとき T1 のどの頂点を T2 のどの頂点と重ねても構わない.T1 を T2 と重ねるのに最小で何回の操作が必要か計算せよ.
(操作): 三角形のうちどれか 1 頂点を選び,それを通る対辺に平行な直線上の任意の点に動かす.
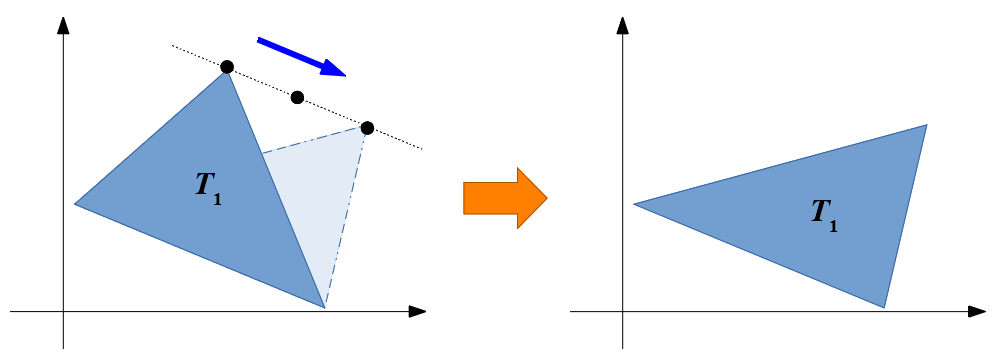
操作の例
下図に Sample Input の最初のデータセットに対してありうる操作列を示す.
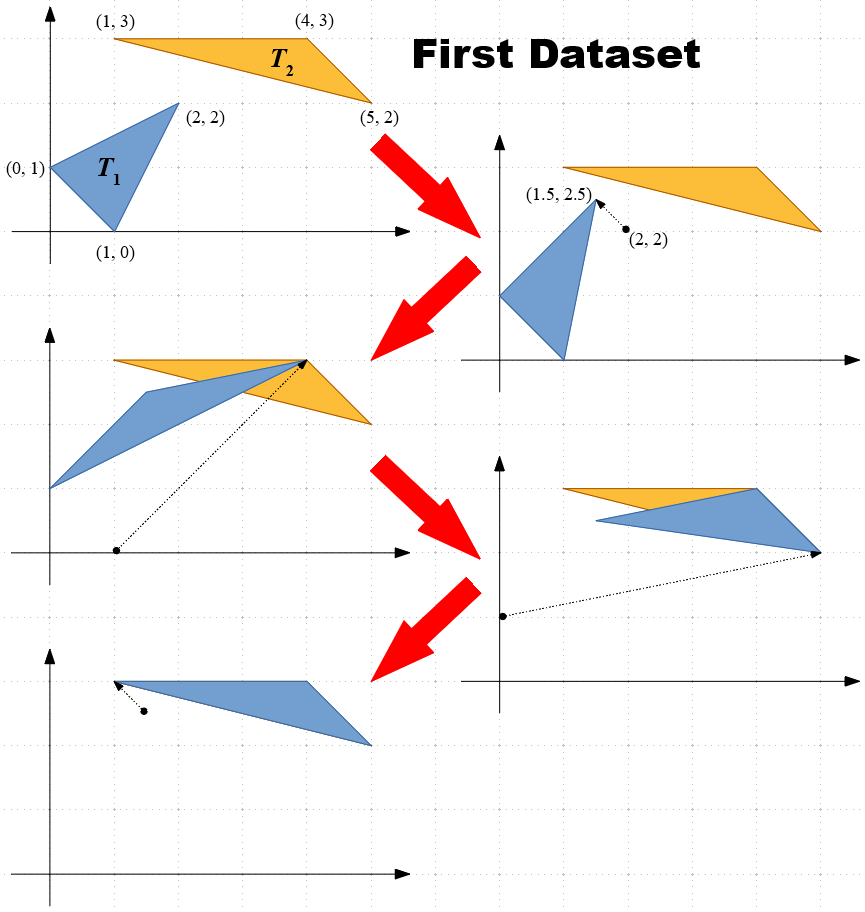
Input
入力は 2000 個以下のデータセットからなる.各データセットは次の形式で表される.
x11 y11
x12 y12
x13 y13
x21 y21
x22 y22
x23 y23
(xij, yij) は Ti の j 番目の頂点の座標を表す.
以下のことが保証される.
- 座標はすべて整数で,絶対値は 1000 以下である.
- T1 と T2 は等しい正の面積を持つ.
- 与えられる 6 つの頂点はすべて相異なる.
データセットの間には空行が 1 つある.
入力の終わりはEOFで表される.
Output
各データセットについて,必要な最小の操作回数を 1 行に出力せよ.5 回以上の操作が必要である場合は Many と出力せよ.
移動した頂点の座標値は整数値とは限らないことに注意せよ.
なお,上記の制約を満たす任意の入力に対して,必要な操作回数はある定数以下であることを証明できる.
Sample Input
0 1 2 2 1 0 1 3 5 2 4 3 0 0 0 1 1 0 0 3 0 2 1 -1 -5 -4 0 1 0 15 -10 14 -5 10 0 -8 -110 221 -731 525 -555 -258 511 -83 -1000 -737 66 -562 533 -45 -525 -450 -282 -667 -439 823 -196 606 -768 -233 0 0 0 1 1 0 99 1 100 1 55 2 354 -289 89 -79 256 -166 131 -196 -774 -809 -519 -623 -990 688 -38 601 -360 712 384 759 -241 140 -59 196 629 -591 360 -847 936 -265 109 -990 -456 -913 -787 -884 -1000 -1000 -999 -999 -1000 -998 1000 1000 999 999 1000 998 -386 -83 404 -83 -408 -117 -162 -348 128 -88 296 -30 -521 -245 -613 -250 797 451 -642 239 646 309 -907 180 -909 -544 -394 10 -296 260 -833 268 -875 882 -907 -423
Output for the Sample Input
4 3 3 3 3 4 4 4 4 Many Many Many Many
