Links
Problem A
所得格差
統計データを処理する際,真っ先に平均値を計算することが多い. 確かに,平均値は,データの傾向を把握するためのよい指標だが,常に最善とは限らない. 場合によっては,平均値がデータの理解を妨げることもある.
たとえば,国民所得を考えてみよう. 所得格差という言葉が示すように,少数の人が国民所得の大部分を得ている国が多い. このような場合,所得の平均値は,大多数の国民の所得よりはるかに高くなってしまう. 平均値を典型的な国民の所得と見なすのは間違いである.
以上のような事情を具体的なデータで検証してみよう. n 人の人の所得 a1,… ,an が与えられる. その中で,平均値 (a1 + … + an) / n 以下の所得の人の人数を答えるプログラムを書いてほしい.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n
a1 a2 … an
データセットは 2 行からなる. 1 行目には国民の人数 n が与えられる. n は整数であり,2 ≤ n ≤ 10 000 が成り立つ. 2 行目には n 人の国民それぞれの所得が与えられる. ai (1 ≤ i ≤ n) が i 人目の国民の所得である. この値は整数であり,1 以上 100 000 以下である.
入力の終わりは,1 個のゼロだけからなる行で表される. 全データセットの n の合計は 50 000 を超えない.
Output
各データセットについて,所得が平均以下の人の人数を出力せよ.
Sample Input
7 15 15 15 15 15 15 15 4 10 20 30 60 10 1 1 1 1 1 1 1 1 1 100 7 90 90 90 90 90 90 10 7 2 7 1 8 2 8 4 0
Output for the Sample Input
7 3 9 1 4
Problem B
折り紙
マスター・グルスは有名な折り紙芸術家であり,折り紙芸術の可能性の探求に熱中している. 将来の創作のために,今は,折り紙の一般理論を目指した基礎的実験を計画しているところである.
実験には長方形の紙を使う. 紙を水平または垂直に何回か折り,その後,折り畳んだ紙を貫通する穴をいくつかあける.
次の図は簡単な実験での紙を折る過程を示している. これは Sample Input の 3 番目のデータセットに対応している. 左上に示す 10 × 8 の長方形の紙を 3 回折ると,右下の 6 × 6 の正方形の形になる. この図では,破線が折り線を表し,弧状の矢印が折る方向を表す. 長方形の大きさと正確な折る場所を示すために,実線が縦横に等間隔で引かれている. そして,長方形領域の色の濃さで,重なった紙の枚数を表している. 折り畳んだ紙の A, B の箇所に穴を貫通させると,紙には全部で 9 つの穴 (A で 8 つ,B で 1 つ) があく.
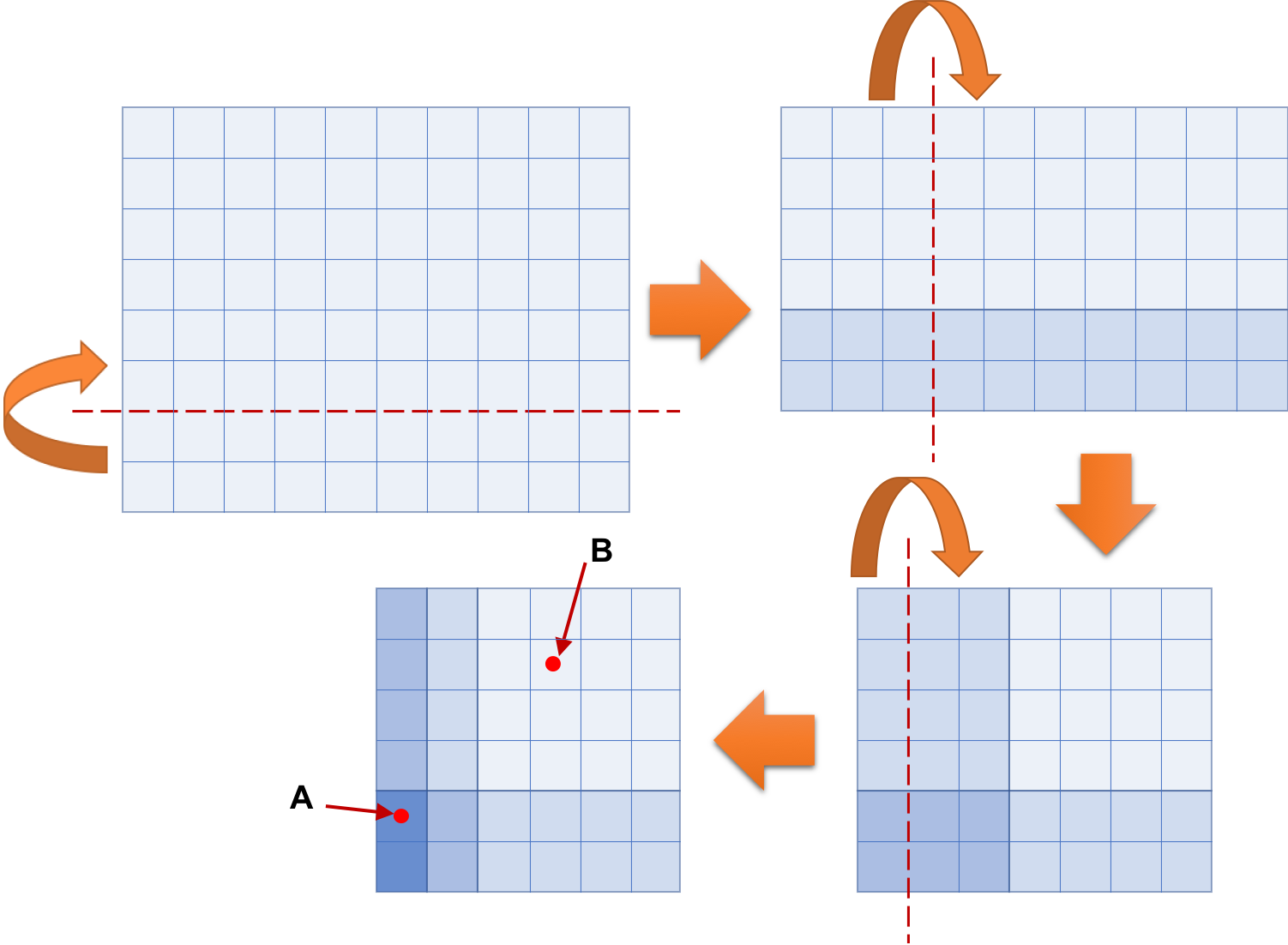
この問題でのあなたの仕事は,長方形の紙と折ったり穴をあけたりする操作に関する情報から,紙に何個の穴があくかを求めるプログラムを作ることである.
Input
入力は高々 1000 個のデータセットからなる. 各データセットは次の形式で表される.
n m t p
d1 c1
...
dt ct
x1 y1
...
xp yp
n, m はそれぞれ長方形の紙の幅と高さであり,32 以下の正整数である. t, p はそれぞれ折る操作と穴をあける操作の回数であり,20 以下の正整数である. di, ci の対で i 番目の折る操作を以下のように定める.
- di は 1 または 2 である.
- ci は正整数である.
- もし di が 1 なら,左端から ci だけ右側を通る垂直の折り線の左側を右側に折り重ねる.
- もし di が 2 なら,下端から ci だけ上側を通る水平の折り線の下側を上側に折り重ねる.
入力の終わりは,4 つのゼロからなる行で表される.
Output
各データセットに対し,p 行の出力を行え. i 行目には i 番目の穴をあける操作で紙にあけられた穴の数を出力すること.
Sample Input
2 1 1 1 1 1 0 0 1 3 2 1 2 1 2 1 0 0 10 8 3 2 2 2 1 3 1 1 0 1 3 4 3 3 3 2 1 2 2 1 1 1 0 1 0 0 0 0 0 0
Output for the Sample Input
2 3 8 1 3 6
Problem C
超高層ビル「みなとハルカス」
ポルト氏は, 1 ギガ階建ての新超高層ビル「みなとハルカス」の何フロアかをオフィスとして賃借し, 新規事業を始める計画だ. 彼は縦方向に連続するなるべく多くのフロアを借りることを要求する. というのは,できるだけ多くの縦に連続した窓に広告を掲示したいのだ. フロアの月額賃料は階数に比例しており, n 階のフロアの賃料は, 1 階の賃料の n 倍である. なお,ここでは地下のフロアは賃借対象外である. ポルト氏を助けるため,あなたには, 月額賃料の総額がポルト氏の予算と ちょうど一致 し, かつ, ポルト氏の要求を満たす縦方向に連続するフロアを見つけるプログラムを書いてほしい.
例えば,予算が 1 階の賃料を単位として 15 単位のときは,4 通りの借り方がある. 1+2+3+4+5, 4+5+6, 7+8, そして 15 である.いずれもその和が 15 になる. もちろんこの場合のフロア数最大の賃借は 1+2+3+4+5 の賃借, すなわち,1 階から 5 階までの賃借である.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
b
データセットは 1 行からなり, ポルト氏の予算が 1 階の賃料の倍数 b として与えられる. b は正の整数であり, 1 < b < 109 を満たす.
入力の終わりは, 1 個のゼロだけからなる行で表される. データセットの総数は 1000 を超えない.
Output
各データセットについてそれぞれ 1 行に, ポルト氏の予算にちょうど一致するように 縦方向に隣接するできるだけ多くのフロアを賃借するやり方を表すふたつの正整数を出力せよ. ひとつ目はフロアのうち最下層の階数,ふたつ目はフロアの総数とせよ.
Sample Input
15 16 2 3 9699690 223092870 847288609 900660121 987698769 999999999 0
Output for the Sample Input
1 5 16 1 2 1 1 2 16 4389 129 20995 4112949 206 15006 30011 46887 17718 163837 5994
Problem D
全チームによるプレーオフ
みなとみらいサッカー連盟が例年主催する選手権は, 参加各チームが他の全チームと 1 試合ずつを行う総当たりリーグ戦で競われる. 他の多くの総当たり形式の大会と違って,この選手権の各試合に引分はない. 規定時間内に決着がつかなければ延長戦, それでも同点ならペナルティキック戦で必ず勝者を決める.
総当たりリーグ戦で勝利数が最多だったチームが複数あれば, そのチーム間で決定戦を行って優勝チームを決める. しかし,チーム数が奇数だったら,全チームが勝敗同数で, 全チームが優勝決定戦に進む可能性もある. ここではこれを「全プレーオフ」と呼ぶ.
今,大会の試合の一部は終わっていて,その勝敗がわかっている. 全プレーオフになるかどうかは残り試合の勝敗にかかっているかもしれない. 全プレーオフになる残り試合の勝敗の組合せパターン数を求めるプログラムを作成せよ.
Sample Input の最初のデータセットは, 次の表のとおりの 5 チームによる総当たり戦の最初の 3 試合の結果を表している. 表中で灰色のセルは未実施の対戦を表している.
 | Team1 | Team2 | Team3 | Team4 | Team5 |
|---|---|---|---|---|---|
| Team1 |  | lost | lost | ||
| Team2 |  | lost | |||
| Team3 | won |  | |||
| Team4 | won |  | |||
| Team5 | won |  |
この場合, 全チームが同勝利数になって全プレーオフになるような残り試合の勝敗の組合せパターンは 以下に示す 2 つだけである. 2 つの表中での違いは黄色で示されている.
 | Team1 | Team2 | Team3 | Team4 | Team5 |
|---|---|---|---|---|---|
| Team1 |  | won | won | lost | lost |
| Team2 | lost |  | lost | won | won |
| Team3 | lost | won |  | won | lost |
| Team4 | won | lost | lost |  | won |
| Team5 | won | lost | won | lost |  |
 | Team1 | Team2 | Team3 | Team4 | Team5 |
|---|---|---|---|---|---|
| Team1 |  | won | won | lost | lost |
| Team2 | lost |  | lost | won | won |
| Team3 | lost | won |  | lost | won |
| Team4 | won | lost | won |  | lost |
| Team5 | won | lost | lost | won |  |
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n
m
x1 y1
...
xm ym
n は 3, 5, 7, 9 のいずれかの奇数で,選手権の参加チーム数を表す. m は既に行われた試合数を表す正の整数であり,n(n−1)/2 より小さい. xi, yi は既に行われた i 番目の試合結果であり, チーム xi がチーム yi を破ったことを表す. xi と yi は, それぞれ 1 以上 n 以下の整数であり,チーム番号を示している. 自チームとの試合はないので, すべての i について xi ≠ yi が成り立つ. また,同じ 2 チームの間の試合結果が入力に複数回現れることはない. すなわち i ≠j ならば (xi,yi)≠ (xj,yj) かつ (xi,yi)≠ (yj,xj) である.
入力の終わりは,1 個のゼロからなる行で表される. データセットの総数は 100 を超えない.
Output
各データセットに対し,全プレーオフになる今後の勝敗の組合せ数を 1 行に出力せよ.
Sample Input
5 3 3 2 4 1 5 1 3 1 1 2 3 2 1 2 3 2 5 4 4 1 4 2 5 1 5 2 5 3 4 1 4 2 5 1 5 4 3 2 4 1 5 1 5 2 9 11 6 1 6 4 7 2 7 3 7 4 8 2 8 3 8 4 9 1 9 3 9 5 9 10 6 1 6 4 7 2 7 3 7 4 8 2 8 3 8 4 9 1 9 3 5 6 4 3 2 1 5 1 2 4 1 3 2 3 9 1 1 2 0
Output for the Sample Input
2 1 0 0 1 0 0 16 0 1615040
Problem E
浮動小数点数
この問題では,コンピュータ上で実数を表現するためのデータ表現形式である浮動小数点数形式を扱う.
指数表記は数を表記する方法の一つで,通常の十進記数法では表しにくい大きな数や小さな数によく用いる. 指数表記では任意の正の実数を m × 10e という形式で表せる. ここで,m (仮数部と呼ばれる) は 1 以上 10 未満の実数であり,e (指数部と呼ばれる) は整数である. 例えば,13.5 という数は 1.35×101 であるので, 仮数部が 1.35,指数部が 1 の指数表記で表せる.
コンピュータで数を扱うには二進数が便利なので,指数表記も 10 の代わりに 2 を基数とする二進指数表記を考える. 二進指数表記では任意の正の実数は m × 2e と表せる.基数が 2 なので,m は 2 未満に制限できる. 例えば,13.5 は 1.6875×23 なので,仮数部が 1.6875,指数部が 3 の二進指数表記で表せる. 仮数部は 1.6875 = 1 + 1/2 + 1/8 + 1/16 なのでこれを小数点以下も二進で表すと 1.10112 となる. 同様に指数部の 3 は 112 である.
浮動小数点数はこの二進指数表記を有限のビット列で表そうとするものである.ビット数の制限によって仮数部の精度が制約され,指数部の範囲が制約されるのはいたしかたないが,広い範囲の実数をある程度高い精度で近似することができる.
この問題では,実際に広く使われているものを簡素化した,1 以上の数だけを表せる 64 ビットの浮動小数点数表現を考える. ここでは最初の 12 ビットを指数部,残る 52 ビットを仮数部に用いる. 浮動小数点数の 64 ビットを b64...b1 と表すことにする. e を最初の 12 ビットを符号なし二進数と解釈した (b64...b53)2 とし, m を残る 52 ビットが表す二進小数に 1 を加えた (1.b52...b1)2 とする. このとき,この浮動小数点数は m × 2e を表す.
以下に 13.5 を上述のフォーマットで表現するビット列を示す.

浮動小数点数の加算操作では,結果を浮動小数点数として表現できる数で近似しなければならない. ここでは近似は切捨てによるものとする.ふたつの浮動小数点数 a と b の和が二進指数表記で a + b = m × 2e (1 ≤ m < 2, 0 ≤ e < 212) と表されるとき,両者の浮動小数点加算操作の結果である浮動小数点数は,12 ビットが e を符号なし二進数で表したもの,残る 52 ビットは m の二進小数部の最初の 52 ビットになる.
この近似手法の欠点として,誤差がすぐ蓄積してしまうことがある. このことを確認するため,ある浮動小数点数を何度も加算する,以下の擬似コードで表される実験をしてみよう. ここで,s も a も共に浮動小数点数であり,個々の加算の結果は前述の方法によって近似するものとする.
s := a
for n times {
s := s + a
}
浮動小数点数 a と繰り返し回数 n が与えられたときこの擬似コードを実行した後の浮動小数点数 s の各ビットを求めよ.
Input
入力は 1000 個以下のデータセットからなる. 各データセットは次の形式で表される.
n
b52...b1
n は繰り返し回数 (1 ≤ n ≤ 1018) を表す. 各 i について,bi は 0 か 1 である. 擬似コード中の浮動小数点数 a は指数部が 0 で,仮数部のビット列が b52...b1 であるようなものとする.
入力の終わりは,ゼロだけからなる行で表される.
Output
各データセットについて,擬似コード実行後の浮動小数点数 s の 64 ビットを 64 個の 0 または 1 の数字の並びとして 1 行に出力せよ.
Sample Input
1 0000000000000000000000000000000000000000000000000000 2 0000000000000000000000000000000000000000000000000000 3 0000000000000000000000000000000000000000000000000000 4 0000000000000000000000000000000000000000000000000000 7 1101000000000000000000000000000000000000000000000000 100 1100011010100001100111100101000111001001111100101011 123456789 1010101010101010101010101010101010101010101010101010 1000000000000000000 1111111111111111111111111111111111111111111111111111 0
Output for the Sample Input
0000000000010000000000000000000000000000000000000000000000000000 0000000000011000000000000000000000000000000000000000000000000000 0000000000100000000000000000000000000000000000000000000000000000 0000000000100100000000000000000000000000000000000000000000000000 0000000000111101000000000000000000000000000000000000000000000000 0000000001110110011010111011100001101110110010001001010101111111 0000000110111000100001110101011001000111100001010011110101011000 0000001101010000000000000000000000000000000000000000000000000000
Problem F
正三角形の柵
三角氏はまっすぐな道に沿った果樹園を所有している. 最近,果樹園の梨を狙ってイノシシが出没するようになったので,彼女は多くの梨の木を護る柵を作ろうと考えた.
果樹園には n 本の梨の木が生えており,梨の生えている場所は 2 次元座標 (x1, y1),..., (xn, yn) で与えられる.簡単のため梨の木の太さは無視する. 三角氏の美学から,柵は正三角形で,一辺は道に平行でなければならない. もちろん反対側の頂点は道から遠い側になくてはならない. 梨の木の位置の座標系は,道が y = 0 となるように設定されており,梨の木は y ≥ 1 にある.
予算の都合から,三角氏は最大 k 本の木は柵の外に残してもよいことにした. この条件で柵の最短長を求めよ.
以下の図は Sample Input の最初のデータセットを表している. 4 本の梨の木が座標 (−1,2), (0,1), (1,2), (2,1) にあり,(−1,2) にある梨の木を柵の外に残すことにすると,周長 6 の正三角形が得られる.
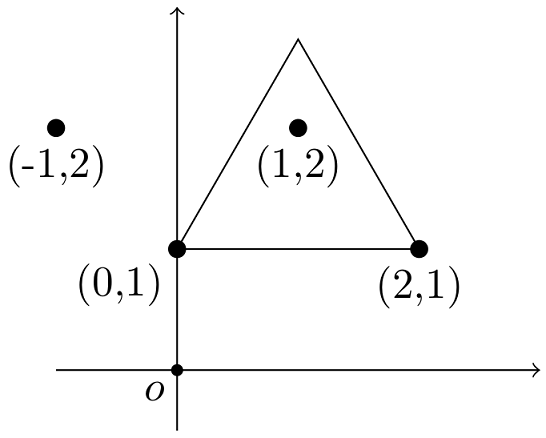
Input
入力は複数のデータセットからなる. 各データセットは以下の形式で表される.
n
k
x1 y1
...
xn yn
各データセットは n+2 行からなる. 1 行目の n は梨の木の本数を表しており,3 ≤ n ≤ 10 000 を満たす. 2 行目の k は柵の外に出てよい梨の木の本数を表しており,1 ≤ k ≤ min(n−2, 5 000) を満たす. 続く n 行は梨の木の座標を表す 2 つの整数 xi, yi からなり,−10 000 ≤ xi ≤ 10 000, 1 ≤ yi ≤ 10 000 が成り立つ. 相異なる 2 本の梨の木が同じ座標をもつことはない.すなわち (xi, yi)=(xj, yj) が成り立つのは i=j の場合に限られる.
入力の終わりは,1 個のゼロだけからなる行で表される. データセットの総数は 100 を超えない.
Output
各データセットについて,柵の最短長を表す数を出力せよ.結果は 10−6 以上の誤差を含んではいけない.
Sample Input
4 1 0 1 1 2 -1 2 2 1 4 1 1 1 2 2 1 3 1 4 4 1 1 1 2 2 3 1 4 1 4 1 1 2 2 1 3 2 4 2 5 2 0 1 0 2 0 3 0 4 0 5 6 3 0 2 2 2 1 1 0 3 2 3 1 4 0
Output for the Sample Input
6.000000000000 6.928203230276 6.000000000000 7.732050807569 6.928203230276 6.000000000000
Problem G
数式探し
一桁の正整数を加算記号 + と乗算記号 * と括弧 ( ) とで組み合わせた数式を考える.数式は,以下の文法規則と開始記号 E で定義される.
E ::= T | E '+' T
T ::= F | T '*' F
F ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9' | '(' E ')'
このような数式を文字列として見たとき,その部分文字列, つまりその文字列中の連続する文字の並びも,また数式として解釈できることがある. 整数 n と数式を表す文字列 s が与えられたとき, s の部分文字列のうち,数式として解釈することができ, 計算すると値が n と一致するものがいくつあるか数えてみよう.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n
s
データセットは 2 行からなる. 1 行目には目標値 n が与えられる. n は整数であり,1 ≤ n ≤ 109 が成り立つ. 2 行目に与えられる文字列 s は上述の文法に従う数式である. s の長さは 2×106 を超えない. また,s の括弧の入れ子の深さは最大で 1000 段である.
入力の終わりはゼロひとつからなる行で表される. 全データセットの s の長さの合計は 5×106 を超えない.
Output
各データセットについて,s の部分文字列のうち, 上記の文法に従っていて数式として計算すると値が n になるものの個数を一行に出力せよ. 同じ文字の並びでも異なる場所にあるものは別々に数えよ.
Sample Input
3 (1+2)*3+3 2 1*1*1+1*1*1 587 1*(2*3*4)+5+((6+7*8))*(9) 0
Output for the Sample Input
4 9 2
Problem H
優秀なプログラマになるには
優秀なプログラマになるためには,数えきれないほどの種類のスキルが必要である. スキルの種類によって重要性は異なっており, プログラミングの総合力は各スキルのレベルと重要性の積の総和で評価される.
あなたはこの夏,夏期プログラミング講習の受講を考えている. 講習には種々のスキルのためのコースがある. あるスキルのためのコースを受講すれば, そのスキルのレベルが払った授業料に比例して, 1 円払うごとに 1 レベルだけ高まるが, スキルのレベルにはそれぞれ上限があり,いくらお金をかけてもそれ以上に高めることはできない. また,各スキルは独立ではなく,最も基礎的なコース以外は, 各コースの受講のためには,その前提となるスキルがあるレベル以上でなければならない.
あなたは限られた予算内でプログラミング総合力評価をできるだけ高めたい.
Input
入力は最大 100 個のデータセットからなる. 各データセットは次の形式で表される.
n k
h1 ... hn
s1 ... sn
p2 ... pn
l2 ... ln
- 1 行目の 2 つの整数は, n がスキルの種類数を表し 2 以上 100 以下, k が使える予算額を表し 1 以上 105 以下である. 以下では各スキルは 1 から n までの番号で表す.
- 2 行目の n 個の整数 h1...hn の各 hi はスキル i のレベルの上限であり, 1 以上 105 以下である.
- 3 行目の n 個の整数 s1...sn の各 si はスキル i の重要度であり, 1 以上 109 以下である.
- 4 行目の n−1 個の整数 p2...pn の各 pi はスキル i の前提となるスキルの番号であり, 1 以上 i 未満である. スキル 1 の前提となるスキルはない.
- 5 行目の n−1 個の整数 l2...ln の各 li はスキル i の習得に最低限必要である前提スキル pi のレベルであり, 1 以上 hpi 以下である.
入力の終わりは,2 つのゼロからなる行で表される.
Output
各データセットについて, 全スキルのレベルがゼロの状態から始めて, 授業料予算の範囲内で到達できる最高のプログラミング総合力評価値, すなわち各スキルのレベルと重要性の積の総和の最大値を, ひとつの整数として1行に出力せよ. 予算は使い切らなくてもかまわない.
Sample Input
3 10 5 4 3 1 2 3 1 2 5 2 5 40 10 10 10 10 8 1 2 3 4 5 1 1 2 3 10 10 10 10 5 10 2 2 2 5 2 2 2 2 5 2 1 1 2 2 2 1 2 1 0 0
Output for the Sample Input
18 108 35
