I am a junior high school teacher. The final examination has just finished, and I have all the students' scores of all the subjects. I want to know the highest total score among the students, but it is not an easy task as the student scores are listed separately for each subject. I would like to ask you, an excellent programmer, to help me by writing a program that finds the total score of a student with the highest total score.

The input consists of multiple datasets, each in the following format.

n m
p_1,1 p_1,2 … p_1,n
p_2,1 p_2,2 … p_2,n
…
p_m,1 p_m,2 … p_m,n

The first line of a dataset has two integers n and m. n is the number of students (1 ≤ n ≤ 1000). m is the number of subjects (1 ≤ m ≤ 50). Each of the following m lines gives n students' scores of a subject. p_j,k is an integer representing the k-th student's score of the subject j (1 ≤ j ≤ m and 1 ≤ k ≤ n). It satisfies 0 ≤ p_j,k ≤ 1000.

The end of the input is indicated by a line containing two zeros. The number of datasets does not exceed 100.

For each dataset, output the total score of a student with the highest total score. The total score s_k of the student k is defined by s_k = p_1,k + … + p_m,k.

5 2
10 20 30 40 50
15 25 35 45 55
6 3
10 20 30 15 25 35
21 34 11 52 20 18
31 15 42 10 21 19
4 2
0 0 0 0
0 0 0 0
0 0

105
83
0

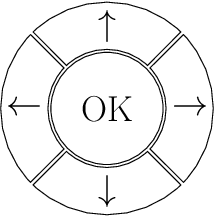
You are to input a string with an OSK (on-screen keyboard). A remote control with five buttons, four arrows and an OK (Fig. B-1), is used for the OSK. Find the minimum number of button presses required to input a given string with the given OSK.

Character to input	Move of highlighted cells	Button presses
I		→,→,→,→,→,→,→,→,OK (9 presses)
C		←,←,←,←,←,←,OK (7 presses)
P		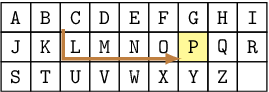↓,→,→,→,→,OK (6 presses)
C		↑,←,←,←,←,OK (6 presses)

The OSK has cells arranged in a grid, each of which has a character in it or is empty. No two of the cells have the same character.

One of the cells of the OSK is highlighted, and pressing the OK button will input the character in that cell, if the cell is not empty.

Initially, the cell at the top-left corner is highlighted. Pressing one of the arrow buttons will change the highlighted cell to one of the adjacent cells in the direction of the arrow. When the highlighted cell is on an edge of the OSK, pushing the arrow button with the direction to go out of the edge will have no effect.

For example, using the OSK with its arrangement shown in Fig. B-2, a string “ICPC” can be input with 28 button presses as shown in Fig. B-3, which is the minimum number of presses.

Characters in cells of the OSKs are any of a lowercase letter (‘a’, ‘b’, ..., ‘z’), an uppercase letter (‘A’, ‘B’, ..., ‘Z’), a digit (‘0’, ‘1’, ..., ‘9’), a comma (‘,’), a hyphen (‘-’), a dot (‘.’), a slash (‘/’), a colon (‘:’), a semicolon (‘;’), or an at sign (‘@’).

The input consists of at most 100 datasets, each in the following format.

h w
r₁
...
r_h
s

The two integers h and w in the first line are the height and the width of the OSK, respectively. They are separated by a space, and satisfy 1 ≤ h ≤ 50 and 1 ≤ w ≤ 50.

Each of the next h lines gives a row of the OSK. The i-th row, r_i is a string of length w. The characters in the string corresponds to the characters in the cells of the i-th row of the OSK or an underscore (‘_’) indicating an empty cell, from left to right.

The given OSK satisfies the conditions stated above.

The next line is a string s to be input. Its length is between 1 and 1000, inclusive. All the characters in s appear in the given OSK. Note that s does not contain underscores.

The end of the input is indicated by a line containing two zeros.

For each dataset, output a single line containing an integer indicating the minimum number of button presses required to input the given string with the given OSK.

3 9
ABCDEFGHI
JKLMNOPQR
STUVWXYZ_
ICPC
5 11
___________
____A______
________M__
___________
_C_________
ACM
4 21
1_2_3_4_5_6_7_8_9_0_-
QqWwEeRrTtYyUuIiOoPp@
AaSsDdFfGgHhJjKkLl;_:
ZzXxCcVvBbNnMm,_._/__
ICPC2019,AsiaYokohamaRegional,QualificationRound
0 0

28
23
493

You, an experimental chemist, have a balance scale and a kit of weights for measuring weights of powder chemicals.

For work efficiency, a single use of the balance scale should be enough for measurement of each amount. You can use any number of weights at a time, placing them either on the balance plate opposite to the chemical or on the same plate with the chemical. For example, if you have two weights of 2 and 9 units, you can measure out not only 2 and 9 units of the chemical, but also 11 units by placing both on the plate opposite to the chemical (Fig. C-1 left), and 7 units by placing one of them on the plate with the chemical (Fig. C-1 right). These are the only amounts that can be measured out efficiently.

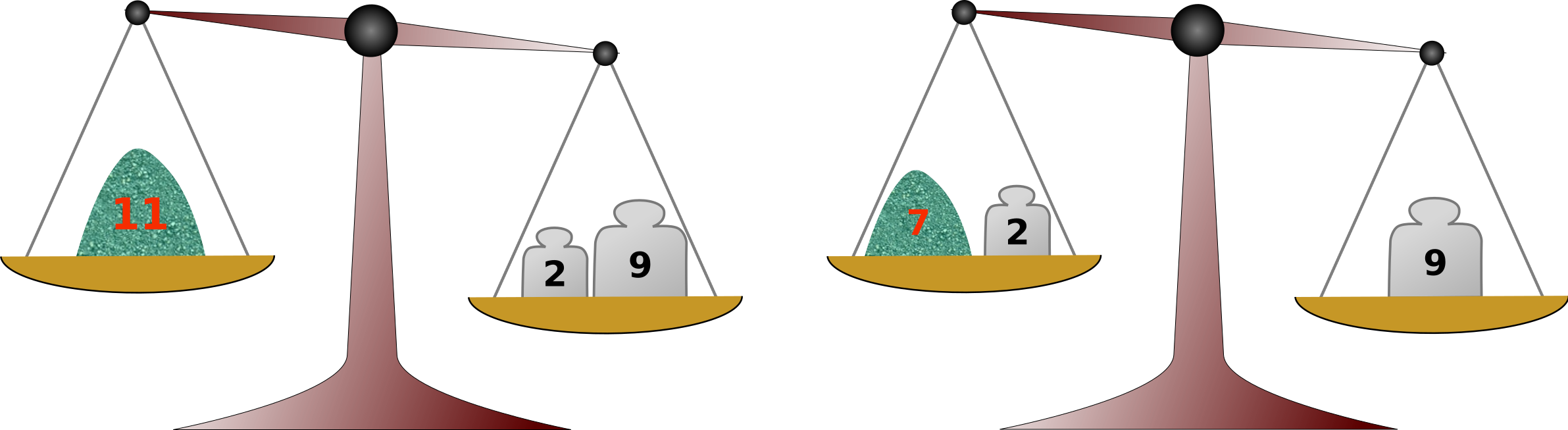
You have at hand a list of amounts of chemicals to measure today. The weight kit already at hand, however, may not be enough to efficiently measure all the amounts in the measurement list. If not, you can purchase one single new weight to supplement the kit, but, as heavier weights are more expensive, you'd like to do with the lightest possible.

Note that, although weights of arbitrary positive masses are in the market, none with negative masses can be found.

The input consists of at most 100 datasets, each in the following format.

n m
a₁ a₂ ... a_n
w₁ w₂ ... w_m

The first line of a dataset has n and m, the number of amounts in the measurement list and the number of weights in the weight kit at hand, respectively. They are integers separated by a space satisfying 1 ≤ n ≤ 100 and 1 ≤ m ≤ 10.

The next line has the n amounts in the measurement list, a₁ through a_n, separated by spaces. Each of a_i is an integer satisfying 1 ≤ a_i ≤ 10⁹, and a_i ≠ a_j holds for i ≠ j.

The third and final line of a dataset has the list of the masses of the m weights at hand, w₁ through w_m, separated by spaces. Each of w_j is an integer, satisfying 1 ≤ w_j ≤ 10⁸. Two or more weights may have the same mass.

The end of the input is indicated by a line containing two zeros.

For each dataset, output a single line containing an integer specified as follows.

• If all the amounts in the measurement list can be measured out without any additional weights, 0.
• If adding one more weight will make all the amounts in the measurement list measurable, the mass of the lightest among such weights. The weight added may be heavier than 10⁸ units.
• If adding one more weight is never enough to measure out all the amounts in the measurement list, -1.

4 2
9 2 7 11
2 9
6 2
7 3 6 12 16 9
2 9
5 2
7 3 6 12 17
2 9
7 5
15 21 33 48 51 75 111
36 54 57 93 113
0 0
  

0
5
-1
5
  

A number of tally counters are placed in a row. Pushing the button on a counter will increment the displayed value by one, or, when the value is already the maximum, it goes down to one. All the counters are of the same model with the same maximum value.

Starting from the values initially displayed on each of the counters, you want to change all the displayed values to target values specified for each. As you don't want the hassle, however, of pushing buttons of many counters one be one, you devised a special tool. Using the tool, you can push buttons of one or more adjacent counters, one push for each, in a single operation. You can choose an arbitrary number of counters at any position in each operation, as far as they are consecutively lined up.

How many operations are required at least to change the displayed values on counters to the target values?

The input consists of multiple datasets, each in the following format.

n m
a₁ a₂ ... a_n
b₁ b₂ ... b_n

Each dataset consists of 3 lines. The first line contains n (1 ≤ n ≤ 1000) and m (1 ≤ m ≤ 10000), the number of counters and the maximum value displayed on counters, respectively. The second line contains the initial values on counters, a_i (1 ≤ a_i ≤ m), separated by spaces. The third line contains the target values on counters, b_i (1 ≤ b_i ≤ m), separated by spaces.

The end of the input is indicated by a line containing two zeros. The number of datasets does not exceed 100.

For each dataset, print in a line the minimum number of operations required to make all of the counters display the target values.

4 5
2 3 1 4
2 5 5 2
3 100
1 10 100
1 10 100
5 10000
4971 7482 1238 8523 1823
3287 9013 9812 297 1809
0 0

4
0
14731

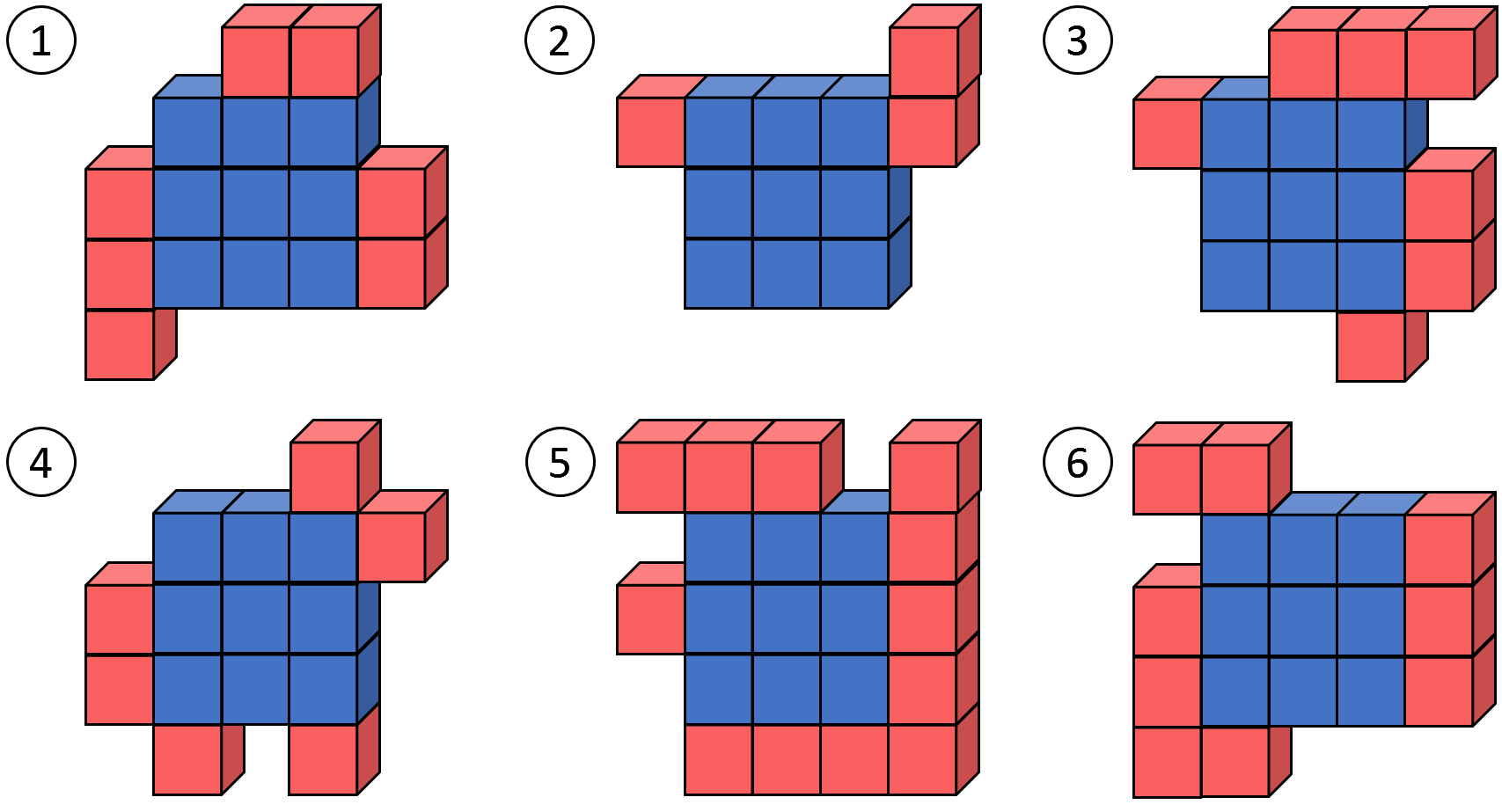
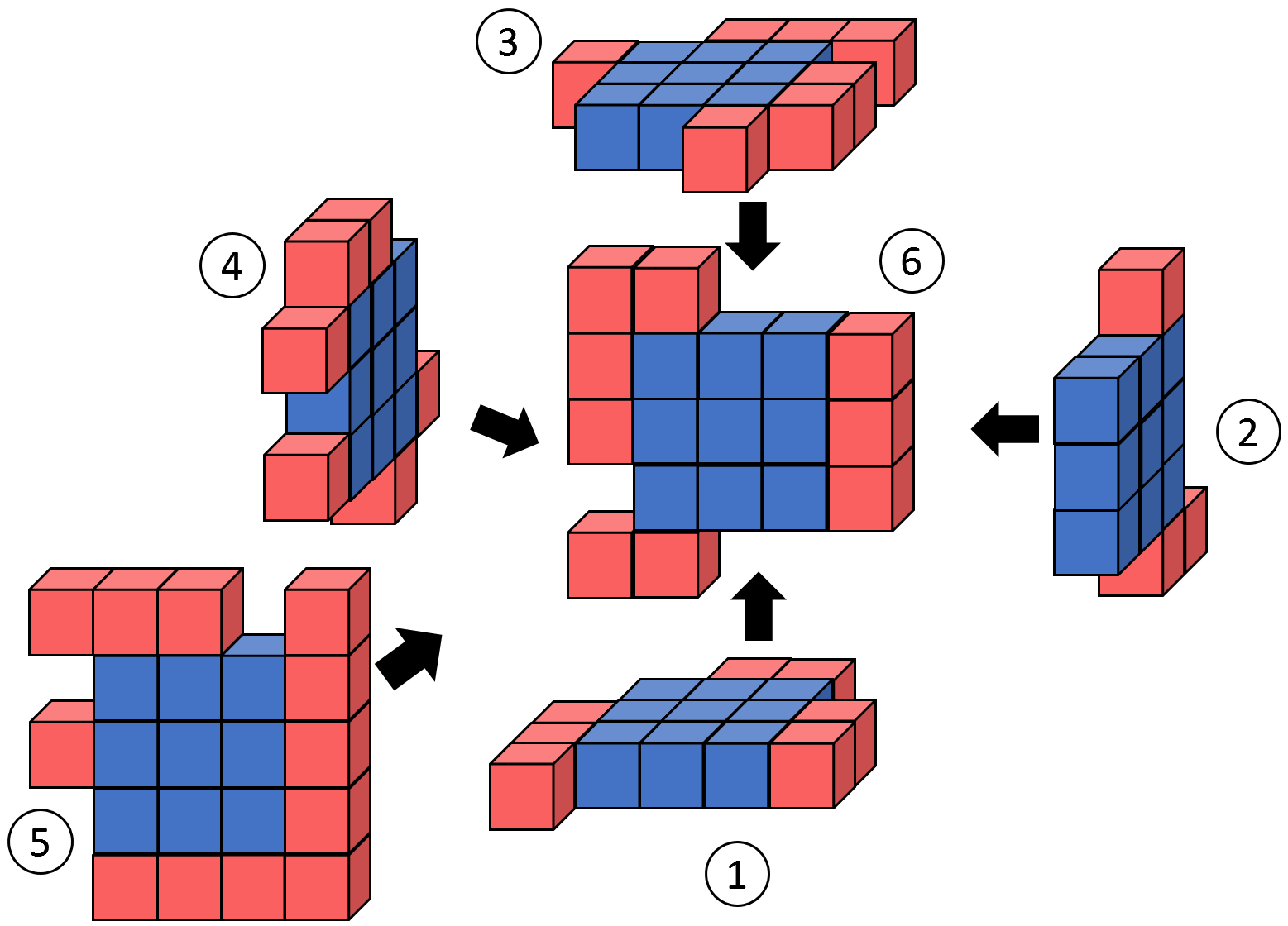
Given a set of six pieces, “Cube Surface Puzzle” is to construct a hollow cube with filled surface. Pieces of a puzzle is made of a number of small unit cubes laid grid-aligned on a plane. For a puzzle constructing a cube of its side length n, unit cubes are on either of the following two areas.

• Core (blue): A square area with its side length n−2. Unit cubes fill up this area.
• Fringe (red): The area of width 1 unit forming the outer fringe of the core. Each unit square in this area may be empty or with a unit cube on it.

Each piece is connected with faces of its unit cubes. Pieces can be arbitrarily rotated and either side of the pieces can be inside or outside of the constructed cube. The unit cubes on the core area should come in the centers of the faces of the constructed cube.

Consider that we have six pieces in Fig. E-1 (The first dataset of Sample Input). Then, we can construct a cube as shown in Fig. E-2.

Mr. Hadrian Hex has collected a number of cube surface puzzles. One day, those pieces were mixed together and he cannot find yet from which six pieces he can construct a cube. Your task is to write a program to help Mr. Hex, which judges whether we can construct a cube for a given set of pieces.

The input consists of at most 200 datasets, each in the following format.

n
x_1,1x_1,2 … x_1,n
x_2,1x_2,2 … x_2,n
…
x_6n,1x_6n,2 … x_6n,n

The first line contains an integer n denoting the length of one side of the cube to be constructed (3 ≤ n ≤ 9, n is odd). The following 6n lines give the six pieces. Each piece is described in n lines. Each of the lines corresponds to one grid row and each of the characters in the line, either ‘X’ or ‘.’, indicates whether or not a unit cube is on the corresponding unit square: ‘X’ means a unit cube is on the column and ‘.’ means none is there.

The core area of each piece is centered in the data for the piece.

The end of the input is indicated by a line containing a zero.

For each dataset, output “Yes” if we can construct a cube, or “No” if we cannot.

5
..XX.
.XXX.
XXXXX
XXXXX
X....
....X
XXXXX
.XXX.
.XXX.
.....
..XXX
XXXX.
.XXXX
.XXXX
...X.
...X.
.XXXX
XXXX.
XXXX.
.X.X.
XXX.X
.XXXX
XXXXX
.XXXX
.XXXX
XX...
.XXXX
XXXXX
XXXXX
XX...
5
..XX.
.XXX.
XXXXX
XXXX.
X....
....X
XXXXX
.XXX.
.XXX.
.....
.XXXX
XXXX.
.XXXX
.XXXX
...X.
...X.
.XXXX
XXXX.
XXXX.
.X.X.
XXX.X
.XXXX
XXXXX
.XXXX
.XXXX
XX...
XXXXX
XXXXX
.XXXX
XX...
0

Yes
No

You are given an undirected complete graph. Every pair of the nodes in the graph is connected by an edge, colored either red or black. Each edge is associated with an integer value called penalty.

By repeating certain operations on the given graph, a “spanning tree” should be formed with only the red edges. That is, the number of red edges should be made exactly one less than the number of nodes, and all the nodes should be made connected only via red edges, directly or indirectly. If two or more such trees can be formed, one with the least sum of penalties of red edges should be chosen.

In a single operation step, you choose one of the nodes and flip the colors of all the edges connected to it: Red ones will turn to black, and black ones to red.

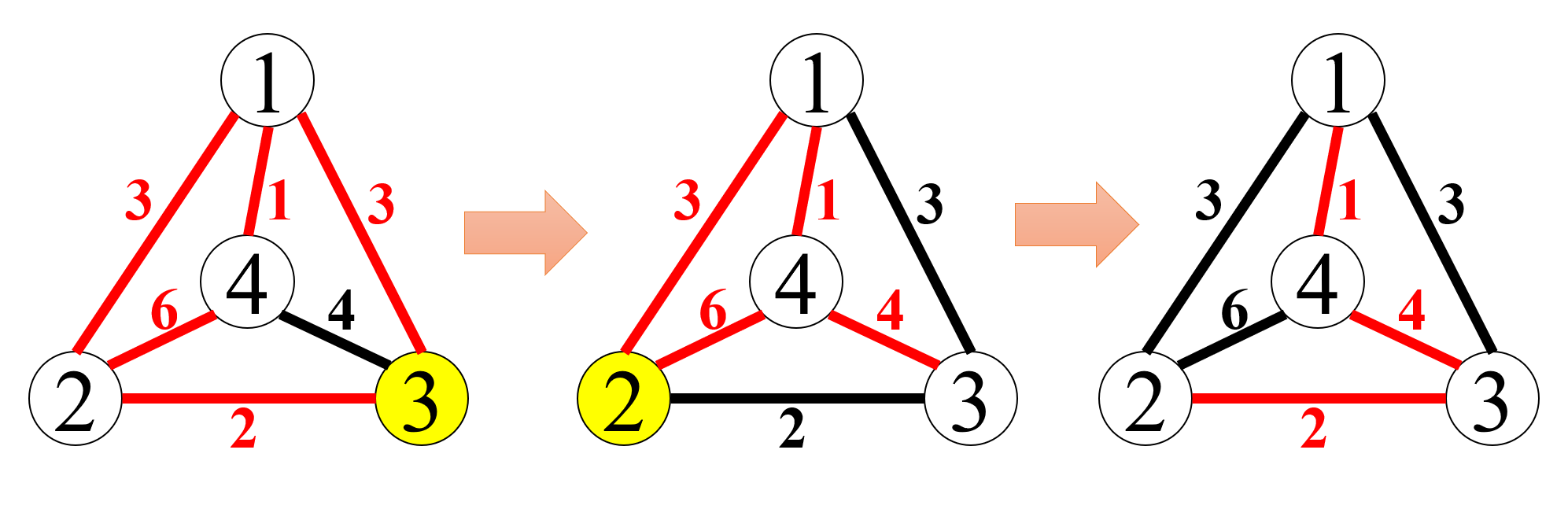
For example, the leftmost graph of Fig. F-1 illustrates the first dataset of Sample Input. By flipping the colors of all the edges connected to the node 3, and then flipping all the edges connected to the node 2, you can form a spanning tree made of red edges as shown in the rightmost graph of the figure.

The input consists of multiple datasets, each in the following format.

n
e_1,2 e_1,3 ... e_1,n-1 e_1,n
e_2,3 e_2,4 ... e_2,n
...
e_n-1,n

The integer n (2 ≤ n ≤ 300) is the number of nodes. The nodes are numbered from 1 to n. The integer e_i,k (1 ≤ |e_i,k| ≤ 10⁵) denotes the penalty and the initial color of the edge between the node i and the node k. Its absolute value |e_i,k| represents the penalty of the edge. e_i,k > 0 means that the edge is initially red, and e_i,k < 0 means it is black.

The end of the input is indicated by a line containing a zero. The number of datasets does not exceed 50.

For each dataset, print the sum of edge penalties of the red spanning tree with the least sum of edge penalties obtained by the above-described operations. If a red spanning tree can never be made by such operations, print -1.

4
3 3 1
2 6
-4
3
1 -10
100
5
-2 -2 -2 -2
-1 -1 -1
-1 -1
1
4
-4 7 6
2 3
-1
0

7
11
-1
9

You have a framed square board forming a grid of square cells. Each of the cells is either empty or with a square tile fitting in the cell engraved with a Roman character. You can tilt the board to one of four directions, away from you, toward you, to the left, or to the right, making all the tiles slide up, down, left, or right, respectively, until they are squeezed to an edge frame of the board.

The figure below shows an example of how the positions of the tiles change by tilting the board toward you.

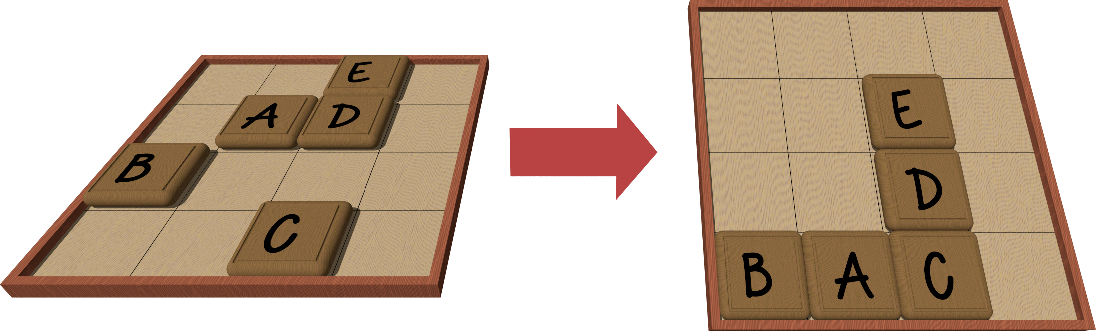
Let the characters U, D, L, and R represent the operations of tilting the board away from you, toward you, to the left, and to the right, respectively. Further, let strings consisting of these characters represent the sequences of corresponding operations. For example, the string DRU means a sequence of tilting toward you first, then to the right, and, finally, away from you. This will move tiles down first, then to the right, and finally, up.

To deal with very long operational sequences, we introduce a notation for repeated sequences. For a non-empty sequence seq, the notation (seq)k means that the sequence seq is repeated k times. Here, k is an integer. For example, (LR)3 means the same operational sequence as LRLRLR. This notation for repetition can be nested. For example, ((URD)3L)2R means URDURDURDLURDURDURDLR.

Your task is to write a program that, given an initial positions of tiles on the board and an operational sequence, computes the tile positions after the given operations are finished.

The input consists of at most 100 datasets, each in the following format.

n
s₁₁ ... s_1n
...
s_n1 ... s_nn
seq

In the first line, n is the number of cells in one row (and also in one column) of the board (2 ≤ n ≤ 50). The following n lines contain the initial states of the board cells. s_ij is a character indicating the initial state of the cell in the i-th row from the top and in the j-th column from the left (both starting with one). It is either ‘.’ (a period), meaning the cell is empty, or an uppercase letter ‘A’-‘Z’, meaning a tile engraved with that character is there.

seq is a string that represents an operational sequence. The length of seq is between 1 and 1000, inclusive. It is guaranteed that seq denotes an operational sequence as described above. The numbers in seq denoting repetitions are between 2 and 10¹⁸, inclusive, and are without leading zeros. Furthermore, the length of the operational sequence after unrolling all the nested repetitions is guaranteed to be at most 10¹⁸.

The end of the input is indicated by a line containing a zero.

For each dataset, output the states of the board cells, after performing the given operational sequence starting from the given initial states. The output should be formatted in n lines, in the same format as the initial board cell states are given in the input.

4
..E.
.AD.
B...
..C.
D
4
..E.
.AD.
B...
..C.
DR
3
...
.A.
BC.
((URD)3L)2R
5
...P.
PPPPP
PPP..
PPPPP
..P..
LRLR(LR)12RLLR
20
....................
....................
.III..CC..PPP...CC..
..I..C..C.P..P.C..C.
..I..C....P..P.C....
..I..C....PPP..C....
..I..C....P....C....
..I..C..C.P....C..C.
.III..CC..P.....CC..
....................
..XX...XX...X...XX..
.X..X.X..X..X..X..X.
....X.X..X..X..X..X.
...X..X..X..X..X..X.
...X..X..X..X...XXX.
..X...X..X..X.....X.
..X...X..X..X.....X.
.XXXX..XX...X...XX..
....................
....................
((LDRU)1000(DLUR)2000(RULD)3000(URDL)4000)123456789012
6
...NE.
MFJ..G
...E..
.FBN.K
....MN
RA.I..
((((((((((((((((((((((((URD)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L
0

....
..E.
..D.
BAC.
....
...E
...D
.BAC
...
..C
.AB
....P
PPPPP
..PPP
PPPPP
....P
....................
....................
....................
....................
....................
XXXX................
PXXXX...............
CXXXX...............
XXXXX...............
XXPCXX..............
CCXXCX..............
CXXXXX..............
CXXXXX..............
CPCIXXX.............
CXPPCXX.............
PCXXXIC.............
CPPCCXI.............
CXCIPXXX............
XCPCICIXX...........
PIPPICIXII..........
......
......
N.....
JNG...
RMMKFE
BEAIFN

Mr. Convexman likes convex polygons very much. During his study on convex polygons, he has come up with the following elegant addition on convex polygons.

The sum of two points in the xy-plane, (x₁, y₁) and (x₂, y₂) is defined as (x₁ + x₂, y₁ + y₂). A polygon is treated as the set of all the points on its boundary and in its inside. Here, the sum of two polygons S₁ and S₂, S₁ + S₂, is defined as the set of all the points v₁ + v₂ satisfying v₁ ∈ S₁ and v₂ ∈ S₂. Sums of two convex polygons, thus defined, are always convex polygons! The multiplication of a non-negative integer and a polygon is defined inductively by 0S = {(0, 0)} and, for a positive integer k, kS = (k - 1)S + S. In this problem, line segments and points are also considered as convex polygons.

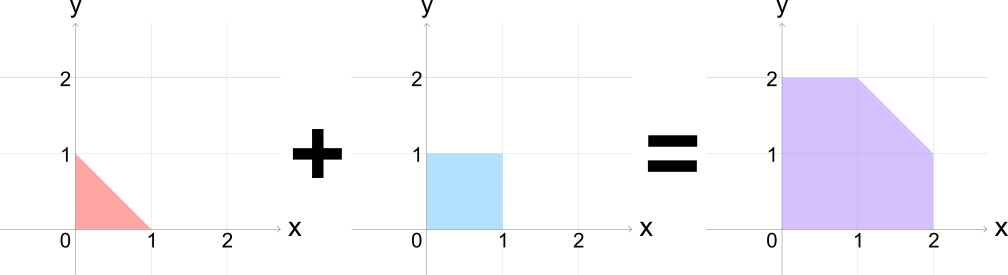
Mr. Convexman made many convex polygons based on two convex polygons P and Q to study properties of the addition, but one day, he threw away by mistake the piece of paper on which he had written down the vertex positions of the two polygons and the calculation process. What remains at hand are only the vertex positions of two convex polygons R and S that are represented as linear combinations of P and Q with non-negative integer coefficients:

R = aP + bQ, and
S = cP + dQ.

Fortunately, he remembers that the coordinates of all vertices of P and Q are integers and the coefficients a, b, c and d satisfy ad - bc = 1.

Mr. Convexman has requested you, a programmer and his friend, to make a program to recover P and Q from R and S, that is, he wants you to, for given convex polygons R and S, compute non-negative integers a, b, c, d (ad - bc = 1) and two convex polygons P and Q with vertices on integer points satisfying the above equation. The equation may have many solutions. Make a program to compute the minimum possible sum of the areas of P and Q satisfying the equation.

The input consists of at most 40 datasets, each in the following format.

n m
x₁ y₁
...
x_n y_n
x'₁ y'₁
...
x'_m y'_m

n is the number of vertices of the convex polygon R, and m is that of S. n and m are integers and satisfy 3 ≤ n ≤ 1000 and 3 ≤ m ≤ 1000. (x_i, y_i) represents the coordinates of the i-th vertex of the convex polygon R and (x'_i, y'_i) represents that of S. x_i, y_i, x'_i and y'_i are integers between −10⁶ and 10⁶, inclusive. The vertices of each convex polygon are given in counterclockwise order. Three different vertices of one convex polygon do not lie on a single line.

The end of the input is indicated by a line containing two zeros.

For each dataset, output a single line containing an integer representing the double of the sum of the areas of P and Q. Note that the areas are always integers when doubled because the coordinates of each vertex of P and Q are integers.

5 3
0 0
2 0
2 1
1 2
0 2
0 0
1 0
0 1
4 4
0 0
5 0
5 5
0 5
0 0
2 0
2 2
0 2
3 3
0 0
1 0
0 1
0 1
0 0
1 1
3 3
0 0
1 0
1 1
0 0
1 0
1 1
4 4
0 0
2 0
2 2
0 2
0 0
1 0
1 2
0 2
4 4
0 0
3 0
3 1
0 1
0 0
1 0
1 1
0 1
0 0

3
2
2
1
0
2