私は，中学校の教師である． ちょうど期末試験が終わったところで，すべての科目について全生徒の点数が手元にある． どれぐらい高い合計点を得た生徒がいるのか知りたいのだが，科目ごとの得点データになっているので，作業が容易でない． そこで，優秀なプログラマであるあなたに手助けしてほしい． 具体的には，合計点が最も高い生徒の合計点を求めるプログラムを書いてほしい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m
p_1,1 p_1,2 … p_1,n
p_2,1 p_2,2 … p_2,n
…
p_m,1 p_m,2 … p_m,n

データセットの最初の行は，二つの整数 n と m からなる． n は生徒の人数 (1 ≤ n ≤ 1000)，m は科目数 (1 ≤ m ≤ 50) である． それに続く m 行のそれぞれには，特定の科目に対する n 人の生徒の得点がある． p_j,k は，生徒 k の科目 j に対する得点を表す整数である (1 ≤ j ≤ m，1 ≤ k ≤ n)． この値は，0 ≤ p_j,k ≤ 1000 を満たす．

入力の終わりは二つのゼロからなる行で表される． データセットの個数は 100 を超えない．

各データセットについて，合計点が最も高い生徒の合計点を出力せよ． 生徒 k の合計点 s_k とは s_k = p_1,k + … + p_m,k のことである．

5 2
10 20 30 40 50
15 25 35 45 55
6 3
10 20 30 15 25 35
21 34 11 52 20 18
31 15 42 10 21 19
4 2
0 0 0 0
0 0 0 0
0 0

105
83
0

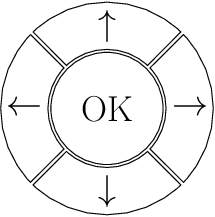
リモコンでスクリーンキーボードを操作して文字列を入力したい. リモコンには 4 方向の矢印と OK のボタンがついている（図 B-1）． 与えられた文字列を与えられたスクリーンキーボードで入力するのに必要な最小ボタン押下回数を求めよ.

入力する文字	強調表示の動き	ボタン操作
I		→,→,→,→,→,→,→,→,OK（9回）
C		←,←,←,←,←,←,OK（7回）
P		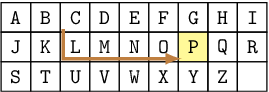↓,→,→,→,→,OK（6回）
C		↑,←,←,←,←,OK（6回）

スクリーンキーボードは格子状に並んだセルからなり, 各セルには文字がひとつあるか空である. 複数のセルが同じ文字を含むことはない．

スクリーンキーボードのセルのひとつは強調表示されていて, 空でないセルが強調表示されているときにリモコンの OK ボタンを押すと, そのセルの文字が入力される.

最初はスクリーンキーボードの左上隅のセルが強調されている． 矢印ボタンのひとつを押すと, 強調セルはその矢印の示す方向の隣のセルに移る. 強調セルがスクリーンキーボードの端にあるときには, スクリーンキーボードから出るような方向の矢印ボタンを押しても何も起きない.

例えば図 B-2 に示すスクリーンキーボード上で文字列 “ICPC” を入力するには, 図 B-3 に示す手順でボタンを 28 回押せばよい. これが最小ボタン押下回数である.

スクリーンキーボードのセルに入っている文字は, 英小文字 (‘a’, ‘b’, ..., ‘z’)， 英大文字 (‘A’, ‘B’, ..., ‘Z’)， 数字 (‘0’, ‘1’, ..., ‘9’)， コンマ (‘,’)， ハイフン (‘-’)， ピリオド (‘.’)， スラッシュ (‘/’)， コロン (‘:’)， セミコロン (‘;’)， アットマーク (‘@’) のいずれかである．

入力は次の形式の最大 100 個のデータセットからなる．

h w
r₁
...
r_h
s

データセットの最初の行のふたつの整数 h と w は，それぞれスクリーンキーボードの高さと幅である．これらは空白で区切られており, 1 ≤ h ≤ 50 と 1 ≤ w ≤ 50 を満たす.

続く h 行に，スクリーンキーボードの各行が与えられる． i 番目の行 r_i はスクリーンキーボードの i 行目を表している． r_i は長さ w の文字列であり，スクリーンキーボードの i 行目の文字が左から順に並んだものである． ただし，スクリーンキーボード上の空のセルは，アンダースコア (‘_’) で表現されている．

スクリーンキーボードは上述の条件を満たす．

続く行の s は，長さ 1 以上 1000 以下の，入力したい文字列である． s に含まれる文字は，必ず与えられたスクリーンキーボード上に存在する． s はアンダースコアを含まないことに注意．

入力の終わりはゼロふたつからなる行で表される．

各データセットについて，与えられた文字列を与えられたスクリーンキーボードで入力するのに必要な最小ボタン押下回数を表す整数ひとつをもつ行を出力せよ．

3 9
ABCDEFGHI
JKLMNOPQR
STUVWXYZ_
ICPC
5 11
___________
____A______
________M__
___________
_C_________
ACM
4 21
1_2_3_4_5_6_7_8_9_0_-
QqWwEeRrTtYyUuIiOoPp@
AaSsDdFfGgHhJjKkLl;_:
ZzXxCcVvBbNnMm,_._/__
ICPC2019,AsiaYokohamaRegional,QualificationRound
0 0

28
23
493

実験化学者のあなたは粉末薬品の計量用に天秤ひとつと分銅のセットを持っている.

作業効率上, 1 回の計量には天秤を 1 回使うだけにしたい. セット中の分銅は同時にいくつ使ってもよく, 天秤の薬品と反対側に置いても同じ側に置いてもよい. たとえば 2 単位と 9 単位の分銅があれば, 2 単位, 9 単位だけでなく, 薬品と反対側に両方の分銅を置けば 11 単位 (図 C-1 左), 片方を薬品と同じ側に置けば 7 単位の薬品を量り取ることができる (図 C-1 右). 効率的に量り取れる量はこれらだけである.

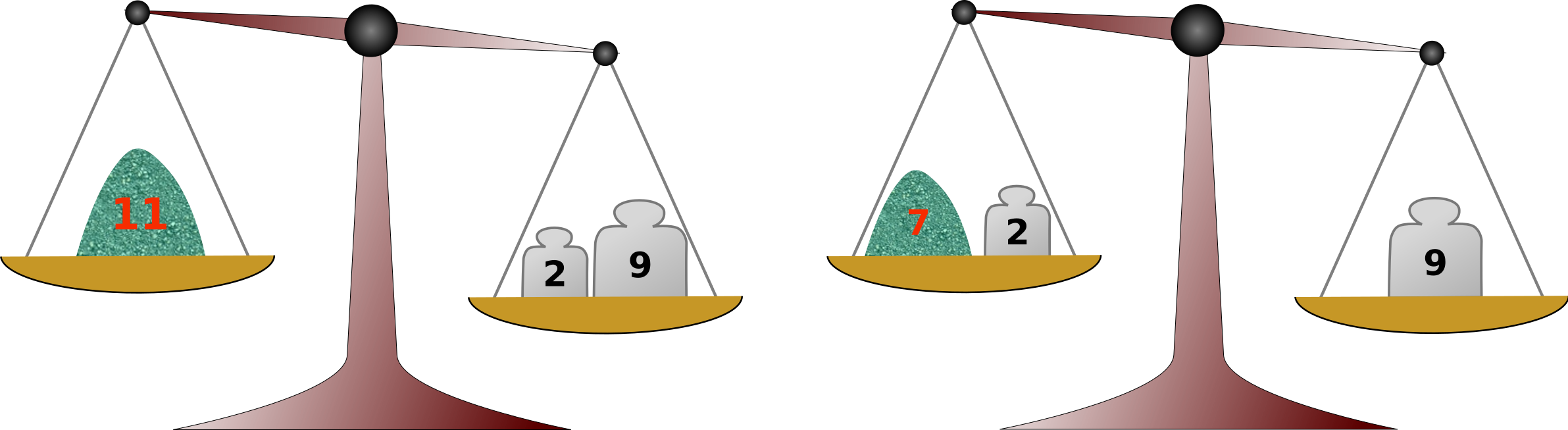
手元に今日計量する薬品量のリストがある. しかし手持ちの分銅セットだけでは, 計量リスト中の量すべてを効率的に量れるとは限らない. その場合はもうひとつだけ分銅を買ってきて補ってもよいのだが, 重い分銅ほど高価なので, なるべく軽いもので済ませたい.

なお, どんな正の重さの分銅でも売っているが, 負の重さのものはない.

入力は次の形式の最大 100 個のデータセットからなる.

n m
a₁ a₂ ... a_n
w₁ w₂ ... w_m

データセットの最初の行の n と m は, それぞれ計量リスト中の薬品量の数とセット中の分銅の個数である. これらは空白で区切られており, 1 ≤ n ≤ 100 と 1 ≤ m ≤ 10 を満たす整数である.

次の行には計量リスト中の n 種の量 a₁ から a_n が空白区切りで並ぶ. 各 a_i は 1 ≤ a_i ≤ 10⁹ を満たす整数で, i ≠ j ならば a_i ≠ a_j である.

データセットの最後の 3 行目には, 手持ちの m 個の分銅の重さ w₁ から w_m が空白区切りで並ぶ. 各 w_j は 1 ≤ w_j ≤ 10⁸ を満たす整数である. 分銅は同じ重さのものがいくつもあるかもしれない.

入力の終わりはゼロふたつからなる行で表される．

各データセットについて以下に指示する整数ひとつからなる 1 行を出力せよ.

• 分銅を追加せずに計量リスト中のすべての量が量り取れるなら 0.
• 分銅ひとつの追加で計量リスト中のすべての量が量り取れるようになるなら, そのような分銅のうちもっとも軽いものの重さ. 追加する分銅は 10⁸ より重くてもよい.
• 分銅ひとつの追加では計量リスト中のすべての量を量り取れるようにならないなら, -1.

4 2
9 2 7 11
2 9
6 2
7 3 6 12 16 9
2 9
5 2
7 3 6 12 17
2 9
7 5
15 21 33 48 51 75 111
36 54 57 93 113
0 0
  

0
5
-1
5
  

計数カウンタが何個か並んでいる． カウンタのボタンを押すと表示されている値が一つ増える． ただし，値が既に最大値なら，値は 1 に戻る． カウンタは全て同じモデルで最大値も同じである．

各カウンタに表示されている値から始めて，各々について指定される目的の値に変えたい． しかし多数のカウンタのボタンを一つ一つ押していくのは面倒なので，特殊な道具を作った． これを使うと，1 回の操作で隣接する一連のカウンタのボタンを 1 回ずつ押せるのだ． 対象とするカウンタの範囲は，操作 1 回ごとにどこからどこまででも自由に決められる．

各カウンタに表示されている値を目的の値に変えるのに最低何回の操作が必要だろうか．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m
a₁ a₂ ... a_n
b₁ b₂ ... b_n

各データセットは 3 行からなる． 1 行目には，カウンタの個数を表す n (1 ≤ n ≤ 1000) と，カウンタに表示される最大値を表す m (1 ≤ m ≤ 10000) が与えられる． 2 行目には，各カウンタの最初の値を表す a_i (1 ≤ a_i ≤ m) が空白区切りで与えられる． 3 行目には，各カウンタの目的の値を表す b_i (1 ≤ b_i ≤ m) が空白区切りで与えられる．

入力の終わりは，二つのゼロからなる行で表される． データセットの個数は 100 を超えない．

各データセットについて，全てのカウンタにそれぞれ目的の値を表示させるのに必要な最小の操作回数を 1 行に出力せよ．

4 5
2 3 1 4
2 5 5 2
3 100
1 10 100
1 10 100
5 10000
4971 7482 1238 8523 1823
3287 9013 9812 297 1809
0 0

4
0
14731

立方体表面パズルとは，6 つのピースを適切に組み合わせて表面に欠けのない中空の立方体を作るパズルである． パズルの各ピースは，単位小立方体を平面上に格子状に並べてできている． 1 辺の長さ n の立方体を作るピースは以下の 2 領域からなる．

• 中央領域 (青): 1 辺の長さ n−2 の正方形領域．単位立方体で埋め尽くされている．
• 周辺領域 (赤): 中央部分の外縁の幅 1 の領域． この領域の単位正方形の上には何もないか，単位立方体があるかである．

各ピースの単位立方体は面でつながっている． 各ピースは自由に回転して使ってよく， 表裏のどちらが組み立てた立方体の内側・外側になってもよい． 各ピースの中央領域上の単位立方体は組み立てた立方体の各面の中央に来なくてはならない．

たとえば，図 E-1 の 6 つのピース (Sample Input の最初のデータセットである) が与えられたとする． このとき，図 E-2 のように組み立てることで立方体を作れる．

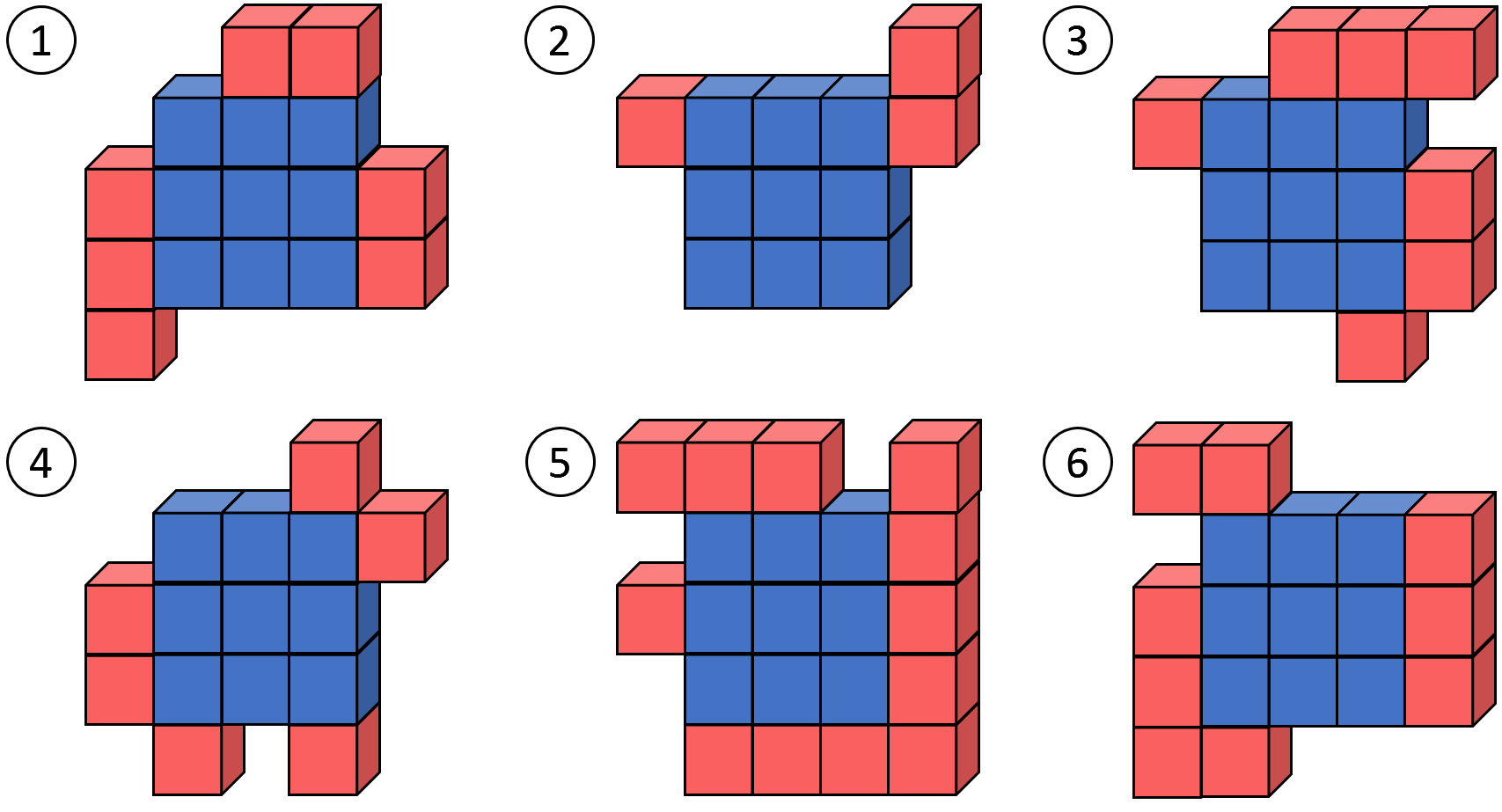
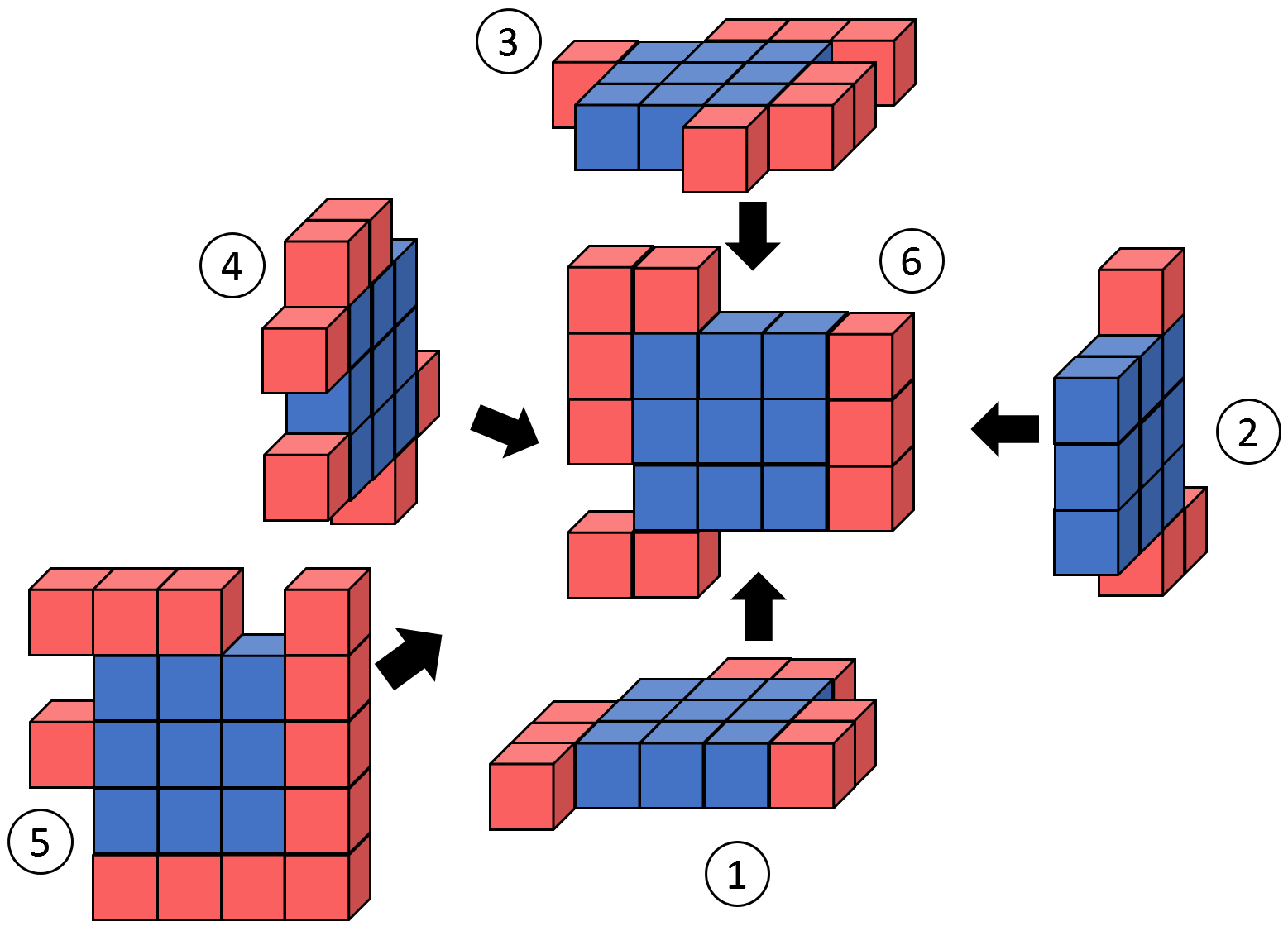
Hadrian Hex 氏はたくさんの立方体表面パズルを収集していた．あるとき，それらのピースが混ざってしまい，どのピースを組み合わせれば立方体を作れるか分からなくなってしまった． そこで，与えられたピースの組合せによって立方体ができるかを判定するプログラムを作って Hex 氏を助けて欲しい．

入力は最大 200 データセットからなり，各データセットは次の形式で表される．

n
x_1,1x_1,2 … x_1,n
x_2,1x_2,2 … x_2,n
…
x_6n,1x_6n,2 … x_6n,n

各データセットの 1 行目には作る立方体の 1 辺の長さ n (3 ≤ n ≤ 9, n は奇数) が与えられる． 続く 6n 行に，6 つのピースが与えられる． 各ピースは n 行で表される． 各行は格子の 1 行に対応し，その行の各文字 (‘X’ または ‘.’) は対応する単位正方形上の単位立方体の有無を意味する． ‘X’ なら単位立方体があり，‘.’ なら空である．

各ピースの中央領域は各ピースのデータの中央に位置する．

入力の終わりは，ゼロだけからなる行で表される．

各データセットについて，立方体ができる場合には “Yes”，できない場合には “No” を出力せよ．

5
..XX.
.XXX.
XXXXX
XXXXX
X....
....X
XXXXX
.XXX.
.XXX.
.....
..XXX
XXXX.
.XXXX
.XXXX
...X.
...X.
.XXXX
XXXX.
XXXX.
.X.X.
XXX.X
.XXXX
XXXXX
.XXXX
.XXXX
XX...
.XXXX
XXXXX
XXXXX
XX...
5
..XX.
.XXX.
XXXXX
XXXX.
X....
....X
XXXXX
.XXX.
.XXX.
.....
.XXXX
XXXX.
.XXXX
.XXXX
...X.
...X.
.XXXX
XXXX.
XXXX.
.X.X.
XXX.X
.XXXX
XXXXX
.XXXX
.XXXX
XX...
XXXXX
XXXXX
.XXXX
XX...
0

Yes
No

無向完全グラフが与えられる． どの頂点どうしもそれぞれ 1 本の赤か黒の辺で結ばれている． 各辺にはペナルティと呼ばれる整数値が設定されている．

このグラフに対してある操作を繰り返すことによって， 赤い辺だけからなる「全域木」を作りたい． すなわち，ちょうど（頂点数 − 1）本の辺だけが赤く， その赤い辺だけで任意の頂点間が直接または間接的につながっているようにしたい． そういう木がいくつも作れるのなら， 赤い辺のペナルティの合計が最小のものを選びたい．

1 回の操作では，頂点をひとつ選び，それに繋がっている全ての辺の色を反転， つまり赤い辺は黒く，黒い辺は赤くする．

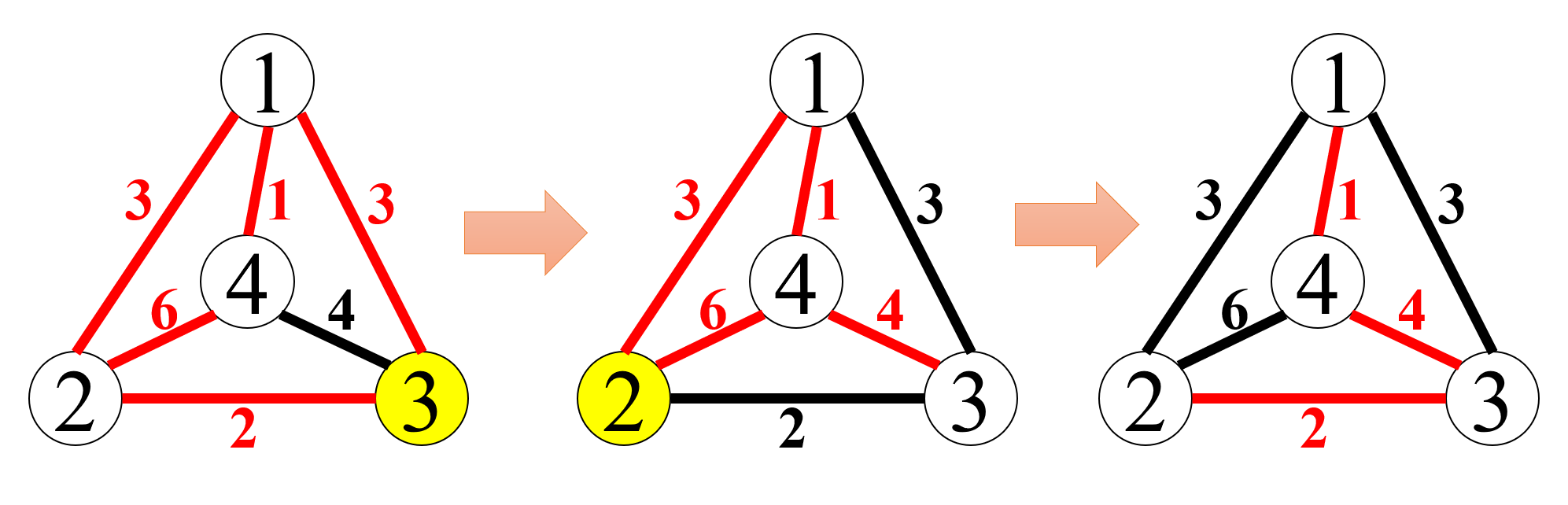
例として， 図 F-1 の左端のグラフはサンプル入力の最初のデータセットを図示したものである． 頂点 3 に繋がる全ての辺の色を反転し，次に頂点 2 に繋がる辺の色を反転することで， 図の右端に示すように赤の辺からなる全域木を構成することができる．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
e_1,2 e_1,3 ... e_1,n-1 e_1,n
e_2,3 e_2,4 ... e_2,n
...
e_n-1,n

整数 n (2 ≤ n ≤ 300) は頂点数を表す． 頂点には 1 から n までの番号がついている． 整数 e_i,k (1 ≤ |e_i,k| ≤ 10⁵) は， 頂点 i と頂点 k を結ぶ辺のペナルティと初期状態での色を表す． 絶対値 |e_i,k| は辺のペナルティを表す． e_i,k > 0 のとき，頂点 i と頂点 k を結ぶ辺の色が初期状態で赤であることを， e_i,k < 0 のとき黒であることを示す．

入力の終わりは，ゼロだけからなる行で表される． データセットの個数は 50 を超えない．

各データセットに対し， 上述の操作で作れる赤い全域木のうちペナルティの合計が最小のものの値を出力せよ． 上述の操作では赤い全域木を作ることができないならば -1 を出力せよ．

4
3 3 1
2 6
-4
3
1 -10
100
5
-2 -2 -2 -2
-1 -1 -1
-1 -1
1
4
-4 7 6
2 3
-1
0

7
11
-1
9

正方形のマス目を描いた枠付きの正方形の盤がある． 各マスは空か，英字を刻印したちょうどマスにはまるタイルがあるかのどちらかである． 盤を向こう側，手前側，左側，右側の 4 方向のいずれかに傾けると， すべてのタイルは盤の枠に押し詰められるまで上下左右に滑っていく．

下図に盤を手前に傾ける前後のタイルの配置の例を示す．

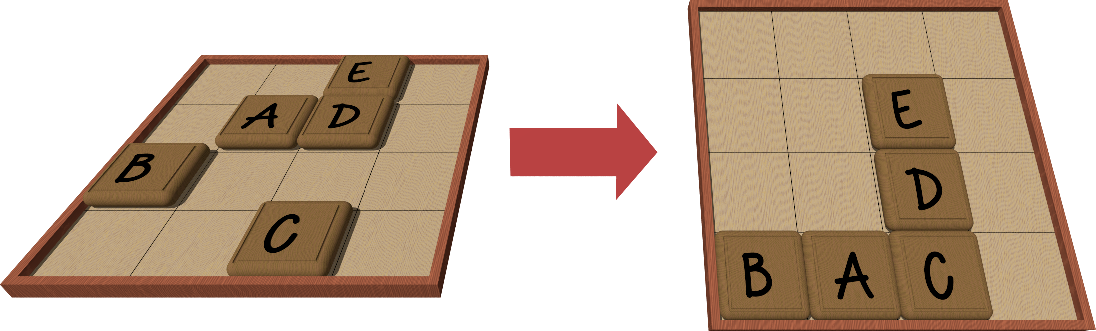
文字 U, D, L, R のそれぞれで，盤を向こう側，手前側，左側，右側に傾ける操作を表すことにしよう． さらに，これらの文字の列で操作の列を表すことにしよう． たとえば文字列 DRU は，盤をまず手前，次に右，最後に向こう側に傾ける一連の操作を表す．タイルは最初に下に，次いで右に，最後に上に動くことになる．

非常に長い操作列を扱うために操作列の繰り返しの表記を使うことにする． ある空ではない操作列 seq を k 回繰り返すことを (seq)k と記す． ここで k は整数である． 例えば (LR)3 は LRLRLR と同じ操作列を表す． 繰り返し表記はネストしていてもよい． 例えば ((URD)3L)2R は URDURDURDLURDURDURDLR を意味する．

タイルの初期位置と操作列が与えられたとき，その操作列に従って操作したあとのタイルの位置を計算するプログラムを書いてほしい．

入力は 100 個以下のデータセットからなる． 各データセットは次の形式で表される．

n
s₁₁ ... s_1n
...
s_n1 ... s_nn
seq

最初の行の n は盤面の 1 行 (および 1 列) に並ぶマス目の数である (2 ≤ n ≤ 50)． 次の n 行は盤上の各マス目の初期状態を表す． s_ij は盤面の上から i 番目，左から j 番目のマス目 (どちらも1から数える) の初期状態を表す文字で，何も置いていないことを表す ‘.’ (ピリオド) であるか，タイルがあることとそこに刻印した文字を表す英大文字 ‘A’-‘Z’ のいずれかである．

seq は操作列を表す文字列である．seq の長さは 1 以上 1000 以下である． seq は上述の規則に従う操作列を表している． seq の中の繰り返し回数を表す数は 0 から始まらない 2 以上 10¹⁸ 以下の整数である． さらに，繰り返し表記をすべて展開した後の操作列の長さも 10¹⁸ 以下になると仮定してよい．

入力の終わりは，ゼロだけからなる行で表される．

各データセットについて，初期状態から始めて指定された操作列に従って操作したあとの各マスの状態を出力せよ． 盤面の状態は入力で盤上のマスの初期状態を与えたのと同じフォーマットで n 行に出力せよ．

4
..E.
.AD.
B...
..C.
D
4
..E.
.AD.
B...
..C.
DR
3
...
.A.
BC.
((URD)3L)2R
5
...P.
PPPPP
PPP..
PPPPP
..P..
LRLR(LR)12RLLR
20
....................
....................
.III..CC..PPP...CC..
..I..C..C.P..P.C..C.
..I..C....P..P.C....
..I..C....PPP..C....
..I..C....P....C....
..I..C..C.P....C..C.
.III..CC..P.....CC..
....................
..XX...XX...X...XX..
.X..X.X..X..X..X..X.
....X.X..X..X..X..X.
...X..X..X..X..X..X.
...X..X..X..X...XXX.
..X...X..X..X.....X.
..X...X..X..X.....X.
.XXXX..XX...X...XX..
....................
....................
((LDRU)1000(DLUR)2000(RULD)3000(URDL)4000)123456789012
6
...NE.
MFJ..G
...E..
.FBN.K
....MN
RA.I..
((((((((((((((((((((((((URD)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L)2L
0

....
..E.
..D.
BAC.
....
...E
...D
.BAC
...
..C
.AB
....P
PPPPP
..PPP
PPPPP
....P
....................
....................
....................
....................
....................
XXXX................
PXXXX...............
CXXXX...............
XXXXX...............
XXPCXX..............
CCXXCX..............
CXXXXX..............
CXXXXX..............
CPCIXXX.............
CXPPCXX.............
PCXXXIC.............
CPPCCXI.............
CXCIPXXX............
XCPCICIXX...........
PIPPICIXII..........
......
......
N.....
JNG...
RMMKFE
BEAIFN

凸郎君は凸多角形が大好きである． 凸郎君は凸多角形を調べているうちに，以下の素敵な凸多角形の加法を思いついた．

xy 平面上の 2 点 (x₁, y₁) と (x₂, y₂) の和を (x₁ + x₂, y₁ + y₂) と定義する． 多角形を，その周上と内部の点すべての集合として扱う． このとき 2 つの多角形 S₁ と S₂ の和 S₁ + S₂ を v₁ ∈ S₁ および v₂ ∈ S₂ を満たす 2 点の和である点 v₁ + v₂ すべての集合と定義する． こう定義すると， 2 つの凸多角形の和が必ず凸多角形になるのだ! 非負の整数と多角形の積を， 0S = {(0, 0)} および正整数 k に対し kS = (k - 1)S + S と帰納的に定める． この問題では線分や一点も凸多角形であるとする．

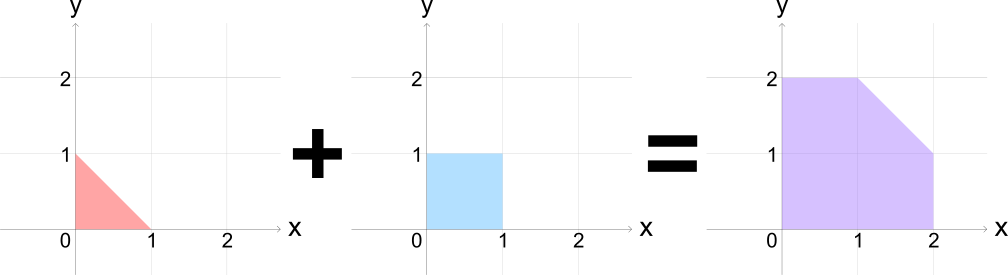
凸郎君はこの加法の性質を調べるため， 2 つの凸多角形 P と Q を基にたくさんの凸多角形を作ってみたが， ある日誤って元の多角形と計算過程を書いた紙を捨ててしまった． 手元に残ったのは P, Q の非負整数係数の線形結合:

R = aP + bQ,
S = cP + dQ,

で表される 2 つの凸多角形 R, S だけである． 幸いにも凸郎君は， P と Q のすべての頂点の座標が整数であることと，係数 a, b, c, d が ad - bc = 1 を満たしていることは覚えていた．

凸郎君は，プログラマーである友人のあなたに R と S から P と Q を復元するプログラムを依頼した． すなわち，凸多角形 R, S が与えられるので，非負の整数 a, b, c, d (ad - bc = 1) と頂点が整数座標の点であるような凸多角形 P, Q で 上の方程式を満たすものを求めてほしいというのである． この方程式は複数の解を持つかもしれない． 方程式を満たす P と Q の面積の和の最小値を求めるプログラムを作成せよ．

入力は高々 40 個のデータセットからなる． 各データセットは次の形式で表される．

n m
x₁ y₁
...
x_n y_n
x'₁ y'₁
...
x'_m y'_m

n は凸多角形 R の頂点の個数を表し， m は凸多角形 S の頂点の個数を表す． n と m は整数であり，3 ≤ n ≤ 1000 および 3 ≤ m ≤ 1000 が成り立つ． (x_i, y_i) は凸多角形 R の i 番目の頂点の座標を表し， (x'_i, y'_i) は凸多角形 S の i 番目の頂点の座標を表す． x_i, y_i, x'_i, y'_i は，それぞれ整数であり −10⁶ 以上，10⁶ 以下である． 凸多角形 R, S の頂点はそれぞれ反時計回りの順番で与えられる． また，1 つの凸多角形の異なる 3 つの頂点は一直線上に並んでいない．

入力の終わりは，2 つのゼロからなる行で表される．

各データセットについて，それぞれ 1 行に P と Q の面積の和の最小値を 2 倍した整数を出力せよ． P と Q の頂点の座標は整数なので，面積の 2 倍は常に整数となることに注意せよ．

5 3
0 0
2 0
2 1
1 2
0 2
0 0
1 0
0 1
4 4
0 0
5 0
5 5
0 5
0 0
2 0
2 2
0 2
3 3
0 0
1 0
0 1
0 1
0 0
1 1
3 3
0 0
1 0
1 1
0 0
1 0
1 1
4 4
0 0
2 0
2 2
0 2
0 0
1 0
1 2
0 2
4 4
0 0
3 0
3 1
0 1
0 0
1 0
1 1
0 1
0 0

3
2
2
1
0
2