The princess has a vast private estate. She has decided to build a new villa there.

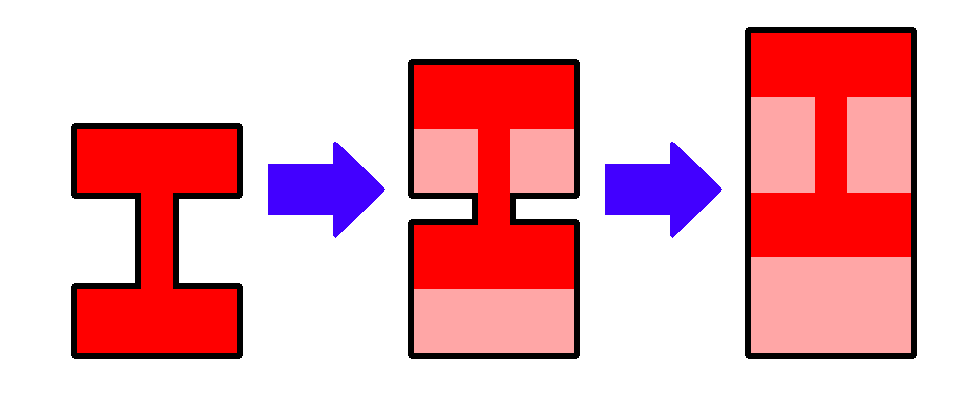
According to her creative request, the ground floor outline of the main house of the villa must be derived from the emblem of the royal family. The emblem is a simple polygon. Four examples are shown in Figure F-1. The outline does not have to be the exact shape of the emblem; it can be formed by sliding and overlaying multiple copies of the emblem, like in Figure F-2. Any finite number of copies can be used, but all the copies should have the same size and orientation without being reversed.

Dataset 1	Dataset 2	Dataset 3	Dataset 4

For security reasons, the outline must be a convex polygon. The rightmost of Figure F-2 is a convex polygon. Your task is to judge whether a convex polygon can be constructed by overlaying a finite number of copies of the emblem.

The input consists of multiple datasets, each in the following format.

n
x₁ y₁
 ⋮
x_n y_n

n is the number of the vertices of the emblem, an integer between 3 and 200, inclusive. (x_i, y_i) gives the coordinates of the i-th vertex in the right-hand coordinate system (i = 1, …, n). Each of x_i and y_i is an integer between −10000 and 10000, inclusive. Any two vertices have different coordinates. The vertices are listed in a counterclockwise order. Any two edges of the emblem do not have a common point other than their connecting vertex. For each vertex, the angle of the two edges is not 180 degrees.

The end of the input is indicated by a line consisting of a zero. The input consists of at most 500 datasets.

For each dataset, output in a line Yes if a convex polygon can be constructed, and No, otherwise.

12
-5 -7
5 -7
5 -3
1 -3
1 3
5 3
5 7
-5 7
-5 3
-1 3
-1 -3
-5 -3
7
0 0
7 1
3 2
2 4
6 9
4 10
1 7
14
0 1
2 0
3 1
2 4
0 4
1 2
-1 1
0 3
-1 4
-2 4
-3 3
-2 -3
-1 -3
0 -2
5
-2 0
1 -4
2 -3
2 3
1 4
0

Yes
No
Yes
Yes