The road network of the city of ICPC forms a grid with east-west and north-south straight streets equidistantly aligned. The streets in the city have serial numbers. For the north-south streets, the street on which the city hall stands is called NS#0, those streets that run east of NS#0 are numbered NS#1, NS#2, and so on, in order from the west, and those streets that run west of NS#0 are numbered NS#−1, NS#−2, and so on, in order from the east. Likewise, for the east-west streets, the street on which the city hall stands is called EW#0, those streets that run north of EW#0 are numbered EW#1, EW#2, and so on, in order from the south, and those streets that run south of EW#0 are numbered EW#−1, EW#−2, and so on, in order from the north. The crossing of NS#x and EW#y is called the crossing (x, y). Moving from the crossing (a, b) to the crossing (c, d) takes time proportional to the Manhattan distance between them, |a−c|+|b−d|.

Every tenth street is a broad street. For x being a multiple of ten, NS#x is a broad street. Likewise, for y being a multiple of ten, EW#y is a broad street. The city of ICPC has a number of landmarks, all of which are located on the crossings of two broad streets.

The city authorities plan to start a number of public bus services. All the services will directly connect pairs of two landmarks. They plan to place a single bus stop at a nearby crossing for each landmark. The bus stop should be on a crossing but not necessarily on a broad street. In other words, for a bus stop on the crossing (x, y), x and y are integers but not necessarily multiples of ten. The Manhattan distance between the bus stop and the corresponding landmark should be less than or equal to a certain upper bound defined for each of the landmarks. This upper bound distance is a multiple of ten. Two or more bus stops for different landmarks can be on the same crossing.

Find the bus stop locations that minimizes the total of the Manhattan distances between pairs of bus stops the bus services connect.

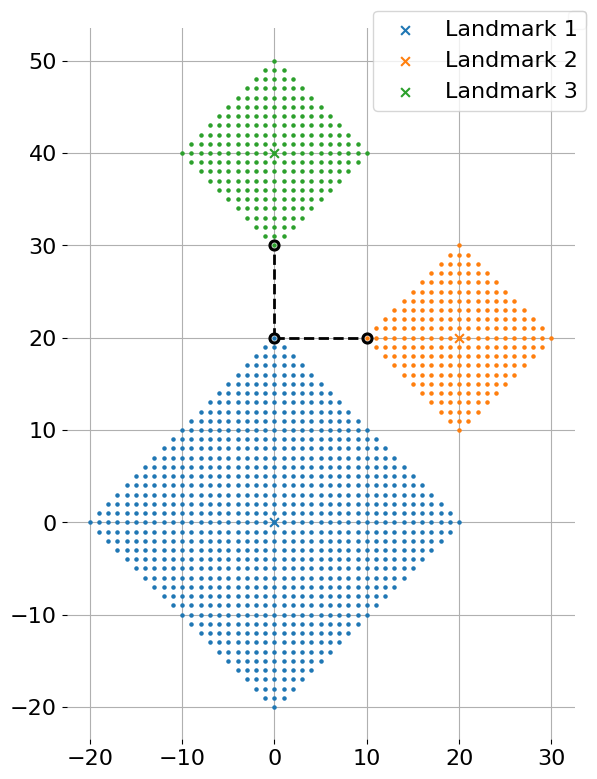
Figure H-1 depicts the first dataset of Sample Input and its optimal solution. The X marks in the figure indicate crossings with landmarks, and the dots indicate crossings where bus stops can be placed. Placing bus stops at crossings with circles is optimal.

The input consists of multiple datasets, each in the following format.

n m
x₁ y₁ r₁
 ⋮
x_n y_n r_n
u₁ v₁
 ⋮
u_m v_m

Here, n is the number of landmarks, satisfying 2 ≤ n ≤ 100, and m is the number of bus services, satisfying 1 ≤ m ≤ n(n−1)/2. The i-th line of the following n lines gives the location of the i-th landmark (x_i, y_i) and the upper bound of the Manhattan distance r_i from the landmark to the corresponding bus stop. Both of x_i and y_i are multiples of ten between −10⁹ and 10⁹, inclusive. r_i is a multiple of ten between 0 and 10⁹, inclusive. The final m lines list bus service plans. The j-th line has two integers u_j and v_j (1 ≤ u_j < v_j ≤ n), which are the landmark numbers between which a bus service is planned. The same pair of landmarks appears at most once.

The end of the input is indicated by a line consisting of two zeros. The number of datasets in the input is at most 50.

For each dataset, output in a line the minimum total of the Manhattan distances between pairs of bus stops the bus services connect.

3 2
0 0 20
20 20 10
0 40 10
1 2
1 3
4 6
0 0 10
0 10 10
10 0 10
10 10 10
1 2
1 3
1 4
2 3
2 4
3 4
4 3
0 0 50
-40 0 10
40 0 10
0 -40 10
1 2
1 3
1 4
0 0

20
0
90