ICPC 市の道路は，市役所を中心に東西・南北に一直線の道路が等間隔に並んだ碁盤目状になっている． 道路には通し番号が振られている． 南北方向の道路の番号は次のように振られている． 市役所のある交差点を通るのが南北 0 号，それより東を通る道路は西から順に南北 1 号，南北 2 号，…，西を通る道路は東から順に南北−1 号，南北−2 号，… である． 東西方向の道路も同様で，市役所のある交差点を通る道路が東西 0 号，それより北を通る道路は南から順に東西 1 号，東西 2 号，…，南を通る道路は北から順に東西−1 号，東西−2 号，… となっている． 以下，南北 x 号と東西 y 号の交差点を交差点 (x, y) と呼ぶ． 2 つの交差点 (a, b) と (c, d) の間の移動には，両者間のマンハッタン距離 |a−c|+|b−d| に比例する時間がかかる．

東西・南北の道路はそれぞれ 10 本ごとに大通りとなっている． すなわち x が 10 の倍数の南北 x 号は大通りである． 同様に y が 10 の倍数の東西 y 号は大通りである． ICPC 市にはいくつかのランドマークがあるが，それらはすべて大通り同士の交差点にある．

市当局はいくつかのバス便を計画している． すべてのバス便は 2 つのランドマーク間を結ぶ直行便とする予定である． 各ランドマークについて，その近辺の交差点にバス停を 1 つ設置する． バス停は交差点になくてはならないが，大通り沿いである必要はない． すなわちバス停を設置する交差点 (x, y) の x, y は整数だが，10 の倍数でなくても良い． バス停とランドマークの間のマンハッタン距離は，ランドマークごとに決められた上限値以下でなければならない． この上限値は 10 の倍数である． 異なるランドマークのためのバス停を同じ交差点に設置しても構わない．

バス便が結ぶバス停間のマンハッタン距離の総和を最小化するようにバス停の設置場所を決めよ．

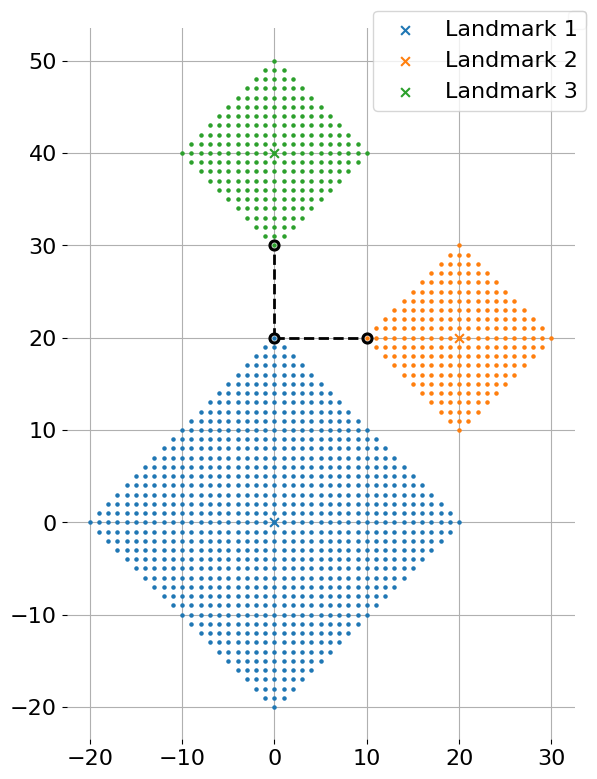
図 H-1 に Sample Input の最初のデータセットとその最適解を示す． 図中のバツ印がランドマークのある交差点を，各ドットがバス停を設置可能な交差点を表す． 丸印の付けられた交差点にバス停を設置するのが最適である．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m
x₁ y₁ r₁
 ⋮
x_n y_n r_n
u₁ v₁
 ⋮
u_m v_m

ここで n はランドマークの数を表し，2 ≤ n ≤ 100 を満たす． m はバス便の数を表し，1 ≤ m ≤ n(n−1)/2 を満たす． 続く n 行のうちの i 行目はランドマーク i の位置 (x_i, y_i) と，そこから対応するバス停までのマンハッタン距離の上限値 r_i を与える． ここで x_i, y_i は −10⁹ 以上 10⁹ 以下の 10 の倍数である． また r_i は 0 以上 10⁹ 以下の 10 の倍数である． 最後の m 行はバス便の一覧である． その j 行目の整数 u_j と v_j (1 ≤ u_j < v_j ≤ n) はランドマーク u_j とランドマーク v_j の間にバス便を予定していることを表す． 同じバス停の組は高々 1 度しか現れない．

入力の終わりは，2 つのゼロからなる行で表される． 入力に含まれるデータセットは 50 個以内である．

各データセットについて，バス便が結ぶバス停間のマンハッタン距離の総和の最小値を 1 行に出力せよ．

3 2
0 0 20
20 20 10
0 40 10
1 2
1 3
4 6
0 0 10
0 10 10
10 0 10
10 10 10
1 2
1 3
1 4
2 3
2 4
3 4
4 3
0 0 50
-40 0 10
40 0 10
0 -40 10
1 2
1 3
1 4
0 0

20
0
90