In ICQC (International Collegiate Quiz Contest), participating teams compete the speed of answering a difficult quiz. The winner is, of course, the team that gives the correct answer first. In addition to this, in the contest this year, a sponsor prize will be provided to the team with the time of giving the correct answer closest to 2023 seconds after the start of the contest.

Given the list of elapsed times from the start of the contest before giving the correct answer for all the participating teams, decide which team is to be provided the sponsor prize.

The input consists of multiple datasets, each in the following format. The number of datasets does not exceed 50.

n
a₁ a₂ ⋯ a_n

The integer n is the number of participating teams within the range between 2 and 100, inclusive. The teams are numbered 1 through n. a_k (k = 1, …, n) is a positive integer not exceeding 10⁴. It represents the elapsed time in seconds before the correct answer was given by the team numbered k. You may assume that one unique team has the elapsed time before answering correctly closest to 2023 seconds.

The end of the input is indicated by a line consisting of a zero.

For each dataset, output in a line the team number of the team to be provided the sponsor prize.

2
123 4567
3
2024 2020 2023
5
2020 2020 2021 2024 2026
3
1599 2222 1599
8
2 2 3 3 4 4 5 1
4
7777 6666 8888 9999
0

1
3
4
2
7
2

Amidakuji is a method of lottery popular in East Asia. It is often used when a number of gifts are distributed to people or when a number of tasks are assigned.

Figure B-1 shows an example of amidakuji, which corresponds to the first dataset of Sample Input. A number of vertical lines are drawn. The number of lines is the same as the number of participants. Some number of horizontal bars are drawn between some pairs of adjacent vertical lines. The number and positions of these bars are arbitrary, but no two bars should share their ends. Usually, many horizontal bars are drawn at random.

To use an amidakuji, first, the names of an item, a gift or a task, are written down at the bottom end of vertical lines. Then, each participant chooses the top end of a vertical line, different from one another. Participants trace down the chosen line from the top. When reaching a T-junction with a horizontal bar, that bar is followed, switching to the adjacent vertical line it is connected, and the trace continues downward. When the bottom end of a vertical line is reached, the item written there is the awarded gift or the assigned task. Figure B-2 shows the case when the top end P is chosen. In this case, the item at R is obtained.

Assume that the participant choosing P of Figure B-2 wants the item at Q, which is not fulfilled. But wait, a special rule just introduced may grant that wish. The new rule allows adding a single horizontal bar at an arbitrary position. Actually, adding a bar marked X in Figure B-3 will make the trace reach Q.

Your task in this problem is to write a program that finds the position of a horizontal bar to add to the given amidakuji for making the trace starting from the top end of the specified vertical line reach the bottom end of the specified vertical line.

The input consists of multiple datasets, each in the following format.

n m p q
x₁ ⋯ x_m

All the input items in a dataset are positive integers. n is the number of vertical lines. m is the number of horizontal bars in the original amidakuji. The participant choosing the top end of the p-th line from the left wants the trace to reach the bottom end of the q-th line from the left. You can assume 2 ≤ n ≤ 50, m ≤ 500, p ≤ n, and q ≤ n hold.

x₁, …, and x_m give the positions of horizontal bars in the original amidakuji. x_k is the position of the k-th bar from the top. Thus, vertical positions of all bars are different. x_k ≤ n − 1 holds. The bar connects the x_k-th line from the left and the (x_k + 1)-th line.

The end of the input is indicated by a line consisting of four zeros. The number of datasets in the input does not exceed 300.

For each dataset, output a single line, which is one of the following.

• If q can be reached from p without adding a bar, OK.
• If not, and adding a single bar cannot make q reachable from p, NG.
• Otherwise, two integers x and y separated by a space, which represent the position of the bar to be added. A bar connecting the x-th line from the left and the (x + 1)-th line should be added at the height between the y-th bar from the top and the (y + 1)-th bar. If the bar is to be added at a position higher than the uppermost bar, y should be 0. If the bar is to be added at a position lower than the lowermost bar, y should be equal to m. If there are two or more appropriate positions to add a bar, the position with the minimum y should be chosen.

OK and NG should be in uppercase.

5 8 3 4
2 1 4 2 3 1 3 2
5 8 3 3
2 1 4 2 3 1 3 2
5 8 3 1
3 1 4 2 2 4 1 3
4 8 1 4
3 1 3 1 3 1 3 1
0 0 0 0

2 6
OK
NG
2 2

You are the teacher of a class of n² pupils at an elementary school. Seats in the classroom are set up in a square shape of n rows (row 1 through row n) by n columns (column 1 through column n).

You are planning a change in the sitting arrangement. In order for your pupils to interact with many different pupils, you want to make those currently on adjacent seats have remote seats.

There is at least one sitting arrangement such that every pair of pupils currently on adjacent seats have seats with the Manhattan distance of no less than ⌊n / 2⌋ between them. Your task is to find such an arrangement. Here, ⌊x⌋ represents the largest integer less than or equal to x. The Manhattan distance of two seats are the sum of the absolute difference of their row numbers and that of their column numbers. Adjacent seats mean those with the Manhattan distance 1.

For example, in the first dataset of Sample Input (n = 4), pupils at the four adjacent seats of the pupil no. 10 are those numbered 6, 9, 11, and 14. In the Output for the Sample Input corresponding to this, their seats have Manhattan distances 3, 3, 2, and 3 from the seat of the pupil no. 10, all of which are ⌊ 4 / 2 ⌋ = 2 or greater. This condition also holds for all the other pupils.

The input consists of multiple datasets, each in the format below. The number of datasets does not exceed 50.

n
a₁₁ a₁₂ ⋯ a_1n
a₂₁ a₂₂ ⋯ a_2n
 ⋮
a_n1 a_n2 ⋯ a_nn

Here, n is the number of rows and also columns of the seats in the classroom (2 ≤ n ≤ 50). The following n lines denote the current sitting arrangement. Each a_ij gives the ID number of the pupil currently sitting in the i-th row from the back and the j-th column from the left, as seen from the teacher's desk. a_ij's are integers 1 through n², without duplicates.

The end of the input is indicated by a line consisting of a single zero.

For each dataset, output a sitting arrangement satisfying the condition stated above in the same format as in the input. If there are two or more such arrangements, any of them will do.

4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
7
1 8 15 22 29 36 43
2 9 16 23 30 37 44
3 10 17 24 31 38 45
4 11 18 25 32 39 46
5 12 19 26 33 40 47
6 13 20 27 34 41 48
7 14 21 28 35 42 49
0

6 1 14 8
16 13 11 9
4 10 2 12
5 3 15 7
4 20 18 44 12 16 36
23 38 40 48 7 39 26
29 9 14 35 37 2 49
13 46 30 5 45 43 24
42 33 17 22 19 27 47
1 3 21 25 11 15 41
31 6 8 34 28 32 10

You are planning a problem set for the upcoming programming contest. The problem set should consist of one or more problems each allocated with a certain amount of points, which is a positive integer. The score of each contestant is the sum of the points of the problems that the contestant correctly answers.

The total of points of problems in the problem set must be equal to the full score given by the contest organizer. In addition, some of the contest sponsor companies want to give special prizes to the contestants first attaining prescribed scores exactly. Thus, you have to make the problem set so that every prize-obtaining score specified by a sponsor can possibly be the score of a contestant at some point of time.

You have not prepared any problems yet, as you are planning to start it after deciding the points of each problem in the set. Because it is troublesome to prepare many problems, you want to meet the above-described requirements with as few problems as possible. For example, when the full score is 7 and the prize-obtaining scores are 2 and 5, you can meet them by preparing two problems with points 2 and 5. When the full score is 7 and the prize-obtaining scores are 2 and 4, however, you have to prepare three problems, e.g., those with points 2, 2, and 3.

Find the minimum possible number of problems that meet the requirements.

The input consists of multiple datasets. Each dataset is in the following format.

n
s

n is the full score of the contest (i.e., the total of points of problems), which is a positive integer not exceeding 100. s represents which values should have possibilities to be contestants' scores. s is a string of length (n + 1) consisting of o's and x's, whose (k + 1)-st character being an o means "contestants should have possibilities to get exactly k points as their scores", and being an x means it is not required, i.e., "either is fine whether contestants can get exactly k points as their scores or not". The first and the last characters of s are always o's.

The end of the input is indicated by a line consisting of a zero. The input consists of at most 100 datasets.

For each dataset, output in a line the minimum possible number of problems that meet the requirements.

3
ooxo
5
oxxxxo
7
oxoxoxxo
7
oxoxxoxo
8
oxxooooxo
0

2
1
3
2
4

In ancient times, the International Collegiate Puzzle Contest (ICPC) was held annually. Each of the annual contests consisted of two rounds: the morning round and the afternoon round. In both of the two rounds, the participants posed one puzzle made on their own to all the other participants, and then tried to solve as many puzzles as possible posed by the other participants.

The participants were ranked by the following rules.

• The participant who solved more puzzles in the afternoon round is ranked higher.
• For participants solving the same number of puzzles in the afternoon round, the one who solved more puzzles in the morning round is ranked higher.
• For participants solving completely the same numbers of puzzles in both rounds, the order is decided by lot.

Recently, a historical document was found, which is said to be the standings of some year's ICPC. As in other similar documents, this document is assumed to list the number of puzzles solved by participants in each round, in the order of their ranks. However, the scholars suspect that someone tampered with the document overwriting some of the numbers. Your task is to find at least how many of the numbers were overwritten, assuming that the original document had records consistent with the rules described above. No parts of the document other than the numbers of puzzles solved were tampered with; addition and deletion of participants were impossible.

The input consists of multiple datasets, each in the following format.

n
x₁ y₁
 ⋮
x_n y_n

n is the number of participants, an integer between 2 and 6000, inclusive.

x_i and y_i are the numbers currently on the document representing the numbers of the puzzles solved in the morning and the afternoon rounds, respectively, by the participant whose rank was the i-th highest. x_i and y_i are non-negative integers less than n. Some of these numbers might differ from the original ones.

The end of the input is indicated by a line consisting of a zero. The input consists of at most 100 datasets. The sum of n's in all the datasets in the input is at most 10⁵.

For each dataset, output in a line at least how many of the 2n numbers in the document were overwritten. Note that the numbers before the overwriting were all non-negative integers less than n.

2
1 0
1 1
3
2 2
2 0
0 1
4
0 3
0 2
3 1
2 0
5
0 3
0 3
1 2
4 2
4 2
3
1 1
2 2
2 2
4
0 0
1 1
2 2
3 3
0

1
1
0
1
2
4

The princess has a vast private estate. She has decided to build a new villa there.

According to her creative request, the ground floor outline of the main house of the villa must be derived from the emblem of the royal family. The emblem is a simple polygon. Four examples are shown in Figure F-1. The outline does not have to be the exact shape of the emblem; it can be formed by sliding and overlaying multiple copies of the emblem, like in Figure F-2. Any finite number of copies can be used, but all the copies should have the same size and orientation without being reversed.

Dataset 1	Dataset 2	Dataset 3	Dataset 4

For security reasons, the outline must be a convex polygon. The rightmost of Figure F-2 is a convex polygon. Your task is to judge whether a convex polygon can be constructed by overlaying a finite number of copies of the emblem.

The input consists of multiple datasets, each in the following format.

n
x₁ y₁
 ⋮
x_n y_n

n is the number of the vertices of the emblem, an integer between 3 and 200, inclusive. (x_i, y_i) gives the coordinates of the i-th vertex in the right-hand coordinate system (i = 1, …, n). Each of x_i and y_i is an integer between −10000 and 10000, inclusive. Any two vertices have different coordinates. The vertices are listed in a counterclockwise order. Any two edges of the emblem do not have a common point other than their connecting vertex. For each vertex, the angle of the two edges is not 180 degrees.

The end of the input is indicated by a line consisting of a zero. The input consists of at most 500 datasets.

For each dataset, output in a line Yes if a convex polygon can be constructed, and No, otherwise.

12
-5 -7
5 -7
5 -3
1 -3
1 3
5 3
5 7
-5 7
-5 3
-1 3
-1 -3
-5 -3
7
0 0
7 1
3 2
2 4
6 9
4 10
1 7
14
0 1
2 0
3 1
2 4
0 4
1 2
-1 1
0 3
-1 4
-2 4
-3 3
-2 -3
-1 -3
0 -2
5
-2 0
1 -4
2 -3
2 3
1 4
0

Yes
No
Yes
Yes

You are serving as the gamemaster of a two-player game in which several cubic dice are used. Each face of the dice has a number on it. Unlike conventional dice, the numbers are not necessarily one through six.

Before starting a game, you select a predefined number of dice from the set of dice at hand and deal them out to the two players. Here, the numbers of dice the two players receive are not necessarily the same, but both players receive at least one die.

Both of the players cast all of the dice dealt in some situations of the game. At that time, the greater the sum of the numbers on the top faces of the dice of a player is, the more advantage the player gains.

For more exciting games, selecting and dealing the dice in a way that achieves the least unfairness is the best.

Definition of the unfairness: Let x denote the sum of the numbers on the top of the dice of one player, and y denote that of the other player. The unfairness is defined as the expected value of (x − y)². Here, each side of a die comes to the top with probability 1/6 independently of the other dice.

Please compute the minimum achievable unfairness with the dice at hand.

The input consists of multiple datasets, each in the following format.

n m
a_1,1 a_1,2 a_1,3 a_1,4 a_1,5 a_1,6
 ⋮
a_n,1 a_n,2 a_n,3 a_n,4 a_n,5 a_n,6

n is the number of dice you have, and m is the number of dice you select to deal to players. n and m are integers that satisfy 2 ≤ m ≤ n ≤ 60. a_i, j gives the number on the j-th face of the i-th die. a_i, j is an integer that satisfies 0 ≤ a_i, j ≤ 60.

The end of the input is indicated by a line consisting of two zeros. The number of datasets does not exceed 100.

For each dataset, output the minimum achievable value of the unfairness multiplied by 36 in a line. Note that this value can be proved to be an integer.

4 3
1 2 3 4 5 6
10 10 10 20 20 20
10 11 12 13 14 15
60 0 60 0 60 0
2 2
0 0 0 0 0 0
60 60 60 60 60 60
8 6
58 43 60 42 53 37
13 41 55 4 21 50
35 13 54 43 24 5
40 60 57 48 60 32
51 32 58 44 60 52
40 29 25 22 0 44
31 22 26 30 49 23
16 34 4 40 21 6
0 0

1146
129600
31878

The road network of the city of ICPC forms a grid with east-west and north-south straight streets equidistantly aligned. The streets in the city have serial numbers. For the north-south streets, the street on which the city hall stands is called NS#0, those streets that run east of NS#0 are numbered NS#1, NS#2, and so on, in order from the west, and those streets that run west of NS#0 are numbered NS#−1, NS#−2, and so on, in order from the east. Likewise, for the east-west streets, the street on which the city hall stands is called EW#0, those streets that run north of EW#0 are numbered EW#1, EW#2, and so on, in order from the south, and those streets that run south of EW#0 are numbered EW#−1, EW#−2, and so on, in order from the north. The crossing of NS#x and EW#y is called the crossing (x, y). Moving from the crossing (a, b) to the crossing (c, d) takes time proportional to the Manhattan distance between them, |a−c|+|b−d|.

Every tenth street is a broad street. For x being a multiple of ten, NS#x is a broad street. Likewise, for y being a multiple of ten, EW#y is a broad street. The city of ICPC has a number of landmarks, all of which are located on the crossings of two broad streets.

The city authorities plan to start a number of public bus services. All the services will directly connect pairs of two landmarks. They plan to place a single bus stop at a nearby crossing for each landmark. The bus stop should be on a crossing but not necessarily on a broad street. In other words, for a bus stop on the crossing (x, y), x and y are integers but not necessarily multiples of ten. The Manhattan distance between the bus stop and the corresponding landmark should be less than or equal to a certain upper bound defined for each of the landmarks. This upper bound distance is a multiple of ten. Two or more bus stops for different landmarks can be on the same crossing.

Find the bus stop locations that minimizes the total of the Manhattan distances between pairs of bus stops the bus services connect.

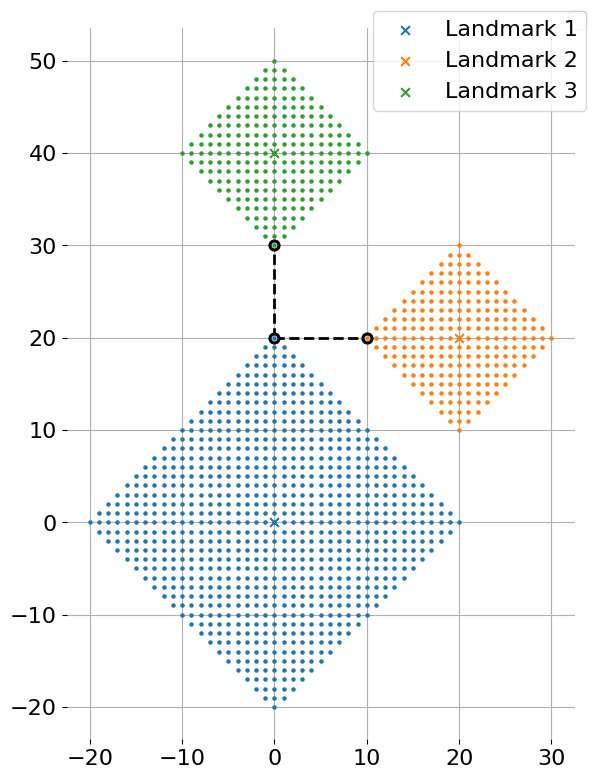
Figure H-1 depicts the first dataset of Sample Input and its optimal solution. The X marks in the figure indicate crossings with landmarks, and the dots indicate crossings where bus stops can be placed. Placing bus stops at crossings with circles is optimal.

The input consists of multiple datasets, each in the following format.

n m
x₁ y₁ r₁
 ⋮
x_n y_n r_n
u₁ v₁
 ⋮
u_m v_m

Here, n is the number of landmarks, satisfying 2 ≤ n ≤ 100, and m is the number of bus services, satisfying 1 ≤ m ≤ n(n−1)/2. The i-th line of the following n lines gives the location of the i-th landmark (x_i, y_i) and the upper bound of the Manhattan distance r_i from the landmark to the corresponding bus stop. Both of x_i and y_i are multiples of ten between −10⁹ and 10⁹, inclusive. r_i is a multiple of ten between 0 and 10⁹, inclusive. The final m lines list bus service plans. The j-th line has two integers u_j and v_j (1 ≤ u_j < v_j ≤ n), which are the landmark numbers between which a bus service is planned. The same pair of landmarks appears at most once.

The end of the input is indicated by a line consisting of two zeros. The number of datasets in the input is at most 50.

For each dataset, output in a line the minimum total of the Manhattan distances between pairs of bus stops the bus services connect.

3 2
0 0 20
20 20 10
0 40 10
1 2
1 3
4 6
0 0 10
0 10 10
10 0 10
10 10 10
1 2
1 3
1 4
2 3
2 4
3 4
4 3
0 0 50
-40 0 10
40 0 10
0 -40 10
1 2
1 3
1 4
0 0

20
0
90