ICQC (International Collegiate Quiz Contest) は，複数のチームがクイズに解答する速さを競うコンテストである． 優勝はもちろん最も早く正答したチームである． さらに今年の大会では，正答したのがコンテスト開始から 2023 秒後に最も近かったチームにスポンサー賞が贈られる．

全参加チームについてのコンテスト開始から正答までの経過時間の一覧を与えられたとき，どのチームにスポンサー賞を贈るのかを決めなさい．

入力は複数のデータセットからなる．データセットの個数は 50 を超えない． 各データセットは次の形式で表される．

n
a₁ a₂ ⋯ a_n

n は参加チーム数を表す，2 以上 100 以下の整数である． チームには 1 から n の番号が振られている． 各 a_k (k = 1, …, n) は 10⁴ を超えない正の整数であり，チーム番号 k のチームが a_k 秒で正答したことを表す． なお，正答までの経過時間が 2023 秒に最も近いチームは 1 つしかないことを仮定してよい．

入力の終わりは，ゼロ 1 つだけからなる行で表される．

各データセットについて，スポンサー賞が贈られるチームの番号を 1 行に出力せよ．

2
123 4567
3
2024 2020 2023
5
2020 2020 2021 2024 2026
3
1599 2222 1599
8
2 2 3 3 4 4 5 1
4
7777 6666 8888 9999
0

1
3
4
2
7
2

あみだくじは，東アジアでよく使われる抽選の方式である． 複数の人に，1 つずつ景品を割り当てたり，仕事を割り振ったりするのによく使われる．

図 B-1 があみだくじの例である (Sample Input の最初のデータセットに対応)． 人数と同じ本数の縦線を平行に引く． そして，いくつかの隣り合う縦線の間に何本かの横線を縦線に垂直に引く． 横線の本数や位置は任意だが，2 本の横線の端点が一致してはならない． 普通は多数の横線をランダムに引く．

あみだくじを使うときは，まず，縦線の下端に景品や仕事の名前を書く． 次に各参加者はそれぞれ違う縦線の上端を選ぶ． そして，選んだ縦線を上端から下向きにたどっていく． 横線との T 字路に達したらその横線を通って反対側の縦線に移り，下に向かっての移動を続ける． 縦線の下端に達したら，そこに書いてある景品や仕事が与えられる． 縦線の上端 P を選んだ場合を図 B-2 に示す． この場合，得られるのは R にある景品や仕事である．

仮に P を選んだ参加者が実は Q にあるものが欲しかったとしたら，それは叶っていない． しかし，待ってほしい． 新設されたばかりの特別ルールによればこの望みは叶えられるかもしれない． 新ルールでは好きな場所に横線を 1 本だけ追加してよいのだ． 実際，図 B-3 のように横線 X を追加すれば Q に行けるではないか．

与えられたあみだくじに 1 本だけ横線を加えて，指定された縦線の上端から指定された縦線の下端に到達するようにするには，横線をどこに加えればよいかを答えるプログラムを書きなさい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m p q
x₁ ⋯ x_m

データセット中の項目は，すべて正の整数である． n は縦線の本数を表す． m は元のあみだくじの横線の本数を表す． 左から p 番目の縦線の上端を選んだ参加者が，左から q 番目の縦線の下端に到達したいものとする． 2 ≤ n ≤ 50，m ≤ 500，p ≤ n，q ≤ n が成り立つと仮定してよい．

x₁, …, x_m は元のあみだくじの横線の位置を表す． x_k が上から k 番目の横線の位置である． x_k ≤ n − 1 が成り立つ． この横線は，左から x_k 番目の縦線と x_k + 1 番目の縦線を結んでいる． この入力形式から，横線の上下方向の位置 (高さ) はすべて異なっていることが保証される．

入力の終わりは，4 つのゼロだけからなる行で表される． 入力中のデータセットの個数は 300 を超えない．

各データセットに対して，次のいずれかからなる行を出力すること．

• 横線を加えなくても p から q に到達する場合，OK．
• そうではなく，1 本の横線をどこに加えても p から q に到達するようにできない場合，NG．
• それ以外の場合，加える横線の位置を表す 2 つの整数 x と y を空白で区切ったもの． 左から x 番目の縦線と x + 1 番目の縦線を結ぶ横線を，上から y 番目の横線と y + 1 番目の横線の間の高さに追加することを意味する． 一番上の横線より上に追加する場合は y = 0 とすること． 一番下の横線より下に追加する場合は y = m とすること． 目的を達する横線の加え方が複数ある場合は，y が最小のものを答えること．

OK と NG は，大文字で出力すること．

5 8 3 4
2 1 4 2 3 1 3 2
5 8 3 3
2 1 4 2 3 1 3 2
5 8 3 1
3 1 4 2 2 4 1 3
4 8 1 4
3 1 3 1 3 1 3 1
0 0 0 0

2 6
OK
NG
2 2

小学校の教師であるあなたは n² 人からなるクラスの担任をしている． 教室の席は n 行 (行番号 1 から n)，n 列 (列番号 1 から n) の正方形に並んでいる．

あなたは席替えを考えている． 生徒にはいろいろな生徒と交流して欲しいので，いま隣り合っている生徒同士は遠い席になるようにしたい．

席がいま隣り合っているどの 2 人の生徒についても，新しい席のマンハッタン距離が ⌊n / 2⌋ 以上になるような席の配置が少なくとも 1 つある． そのような配置を 1 つ見つけて欲しい． ここで ⌊x⌋ は x 以下の最大の整数を表す． 2 つの席の間のマンハッタン距離とは，両者の行番号の差の絶対値と列番号の差の絶対値を足し合わせたものである． また，隣り合う席とはマンハッタン距離が 1 の席同士のことをいう．

たとえば，Sample Input の最初のデータセット (n = 4) で，10 番の生徒の隣には，6, 9, 11, 14 番の 4 人の生徒がいる． これら 4 人の席替え後 (Output for the Sample Input) の 10 番からのマンハッタン距離は，それぞれ 3, 3, 2, 3 で，いずれも ⌊ 4 / 2 ⌋ = 2 以上になっている． 他のどの生徒についても，条件が満たされている．

入力は複数のデータセットからなり，各データセットは以下の形式で表される． データセットの個数は 50 を超えない．

n
a₁₁ a₁₂ ⋯ a_1n
a₂₁ a₂₂ ⋯ a_2n
 ⋮
a_n1 a_n2 ⋯ a_nn

ここで n は教室の席の行の数であり列の数でもある (2 ≤ n ≤ 50)． 続く n 行は現在の席の配置を表す． 各 a_ij は，教卓から見て奥から i 番目の列，左から j 番目の行の席に座っている生徒の出席番号である． a_ij は 1 から n² までの整数であり，重複はない．

入力の終わりは，ゼロだけからなる行で表される．

各データセットについて，上述の条件を満たす席の配置を入力中の席の配置と同じ形式で出力せよ． 条件を満たす配置が複数ある場合は，どれを答えても良い．

4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
7
1 8 15 22 29 36 43
2 9 16 23 30 37 44
3 10 17 24 31 38 45
4 11 18 25 32 39 46
5 12 19 26 33 40 47
6 13 20 27 34 41 48
7 14 21 28 35 42 49
0

6 1 14 8
16 13 11 9
4 10 2 12
5 3 15 7
4 20 18 44 12 16 36
23 38 40 48 7 39 26
29 9 14 35 37 2 49
13 46 30 5 45 43 24
42 33 17 22 19 27 47
1 3 21 25 11 15 41
31 6 8 34 28 32 10

あなたは来たるプログラミングコンテストの問題セットを検討中である． 問題セットは，それぞれ正整数の配点を定めた 1 つ以上の問題で構成される． 各参加者の得点は，その参加者が正解した問題の配点の総和とする．

問題セットの配点の合計はコンテスト主催者の定めた満点に等しくなければならない． また，コンテストのスポンサー企業のいくつかは，特定の得点ちょうどに最初に到達した参加者に特別賞を与えたいという． このために，スポンサー特別賞の対象となる全ての得点について，それらがある時点での参加者の得点となり得るように問題セットを構成する必要がある．

あなたはまだ問題を 1 つも準備しておらず，問題セットの配点を決めた後で準備を始めるつもりである． 問題をたくさん準備するのは大変なので，なるべく少ない問題数で上記の要件を満たしたい． たとえば，満点が 7 点で特別賞得点が 2 点と 5 点である場合，配点が 2 点の問題と 5 点の問題を 1 つずつ準備すれば，2 問で要件を満たせる． 一方，満点が 7 点で特別賞得点が 2 点と 4 点である場合，3 問（たとえば，配点が 2 点の問題 2 つと 3 点の問題 1 つ）が必要となる．

要件を満たすような問題数の最小値を求めよ．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
s

n はコンテストの満点（全問題の配点の合計）を表す． n は正の整数であり，100 を超えない． s は参加者の得点として現れ得るべき値を表す． s は o, x からなる長さ (n + 1) の文字列であり，その (k + 1) 文字目は「参加者がちょうど k 点を獲得可能でなければならない」場合に o，その必要はない，すなわち「参加者がちょうど k 点を獲得可能でも不可能でも構わない」場合に x である． s の最初と最後の文字は必ず o である．

入力の終わりは，1 つのゼロからなる行で表される． 入力に含まれるデータセットは 100 個以下である．

各データセットについて，要件を満たすような問題数の最小値を 1 行に出力せよ．

3
ooxo
5
oxxxxo
7
oxoxoxxo
7
oxoxxoxo
8
oxxooooxo
0

2
1
3
2
4

太古の昔， International Collegiate Puzzle Contest (ICPC) というパズル大会が毎年開催されていた． 各大会は午前・午後の 2 つのラウンドで構成されていた． どちらのラウンドでも，参加者はまず自作のパズル 1 つを他の全参加者に提示し，その後に自分自身以外の全参加者が提示したパズルをできるだけ多く解こうとした．

参加者の順位は以下の規則に従って決めていた．

• 午後のラウンドで解いたパズルの数がより多い参加者がより上位となる．
• 午後のラウンドで同数のパズルを解いた参加者のなかでは，午前のラウンドで解いたパズルの数がより多い方が上位となる．
• 両ラウンドで解いたパズルの数が完全に一致する参加者同士の順位はくじびきで決める．

先日，ある年の ICPC の順位表とされる文書が発見された． 他の同様の資料から，この文書は各ラウンドで解いたパズルの数を上位の参加者から順に書き並べたものと考えられる． ところが学者たちは文書は何者かによって改竄されていて，いくつかの数が書き換えられているのではないかという疑いを持っている． もともとの順位表に上述の規則と矛盾がなかったと仮定したとき，少なくともいくつの数が書き換えられているのかを求めてほしい． なお，文書中の解いたパズルの数以外の部分への改竄はなく，参加者の追加や削除もありえない．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
x₁ y₁
 ⋮
x_n y_n

n は参加者数を表す 2 以上 6000 以下の整数である．

x_i と y_i は，それぞれ順位が i 位の参加者が午前と午後に解いたパズルの数として現在文書に記載されている値を表す． x_i と y_i はそれぞれ 0 以上 n 未満の整数である． これらの値のいくつかは，本来の値から改竄された結果である可能性がある．

入力の終わりは，1 つのゼロからなる行で表される． 入力に含まれるデータセットは 100 個以下である． また，全てのデータセットにおける n の合計は 10⁵ を超えない．

各データセットについて，文書に記された 2n 個の数値のうち，もとの順位表から書き換えられたものの個数としてありうる最小値を 1 行に出力せよ． 書き換えが行われる前の数値は全て 0 以上 n 未満であったことに注意されたい．

2
1 0
1 1
3
2 2
2 0
0 1
4
0 3
0 2
3 1
2 0
5
0 3
0 3
1 2
4 2
4 2
3
1 1
2 2
2 2
4
0 0
1 1
2 2
3 3
0

1
1
0
1
2
4

お姫様は広大な私有地を持っており，そこに新たに別荘を建設することにした．

お姫様の発案で，別荘の母屋の 1 階部分を王家の紋章に由来する外形とすることになった． 紋章は単純多角形である．紋章の例を 4 つ図 F-1 に示す． 外形は必ずしも紋章と同じ形である必要はなく，図 F-2 のように紋章の複製を複数個ずらして重ね合わせた図形でも良い．有限個ならいくつの複製を重ね合わせてもよいが，全ての複製は同じ大きさかつ同じ向きでなければならず，裏返してはいけない．

データセット 1	データセット 2	データセット 3	データセット 4

防犯上，外形は凸多角形にしたい．図 F-2 の右端の図形は凸多角形になっている． あなたの仕事は，紋章を有限個重ね合わせることで凸多角形を作成できるかを判定することだ．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n
x₁ y₁
 ⋮
x_n y_n

n は紋章を構成する頂点の個数で，3 以上 200 以下の整数である．(x_i, y_i) は右手座標系で i 番目の頂点の座標を表す (i = 1, …, n)．x_i と y_i は，それぞれ整数であり，−10000 以上 10000 以下である．頂点同士の座標は異なり，反時計回り順に与えられる．紋章を構成する辺同士は接続する頂点以外に共有点を持たない．また，どの頂点でも辺同士のなす角度が 180 度ではない．

入力の終わりは，1 つのゼロだけからなる行で表される．データセットの個数は 500 を超えない．

各データセットについて，凸多角形を作成できるならば Yes を，できないならば No を 1 行に出力せよ．

12
-5 -7
5 -7
5 -3
1 -3
1 3
5 3
5 7
-5 7
-5 3
-1 3
-1 -3
-5 -3
7
0 0
7 1
3 2
2 4
6 9
4 10
1 7
14
0 1
2 0
3 1
2 4
0 4
1 2
-1 1
0 3
-1 4
-2 4
-3 3
-2 -3
-1 -3
0 -2
5
-2 0
1 -4
2 -3
2 3
1 4
0

Yes
No
Yes
Yes

あなたはサイコロをいくつか使う 2 人用ゲームのゲームマスターである． サイコロは立方体で，各面に数が 1 つ記されている． 普通のサイコロとは違い，これらの数は 1 から 6 とは限らない．

ゲームを始めるにあたり，手元のサイコロの中からある決まった個数のサイコロを選び，選んだサイコロを残らず 2 人のプレイヤに分配する． 両プレイヤが受け取るサイコロが同数であるとは限らないが，どちらのプレイヤも少なくとも 1 つのサイコロを受け取る．

このゲームには両プレイヤが配られたサイコロをすべて振る場面がある． そのとき，プレイヤの振ったサイコロの出目の合計が大きいほど，そのプレイヤはゲームで有利になる．

ゲームを盛り上げるためには，不公平度が最小となるようにサイコロを選んで配るのが最良である．

不公平度の定義: 一方のプレイヤのサイコロの出目の合計を x, もう一方のプレイヤの方を y とする． 不公平度を (x − y)² の期待値と定義する． ここで，サイコロの各面は他のサイコロとは独立に 1/6 の確率で出るものとする．

手元のサイコロで達成可能な不公平度の最小値を計算してほしい．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m
a_1,1 a_1,2 a_1,3 a_1,4 a_1,5 a_1,6
 ⋮
a_n,1 a_n,2 a_n,3 a_n,4 a_n,5 a_n,6

n はあなたの手元にあるサイコロの個数を，m はプレイヤに配るために選ぶサイコロの個数を表す． n, m は整数であり，2 ≤ m ≤ n ≤ 60 を満たす． a_i, j は i 番目のサイコロの j 番目の面に記された数を表す． a_i, j は整数であり，0 ≤ a_i, j ≤ 60 を満たす．

入力の終わりは，ゼロ 2 つからなる行で表される． データセットの個数は 100 を超えない．

各データセットについて，達成可能な不公平度の最小値の 36 倍 を 1 行に出力せよ． なお，この値は整数となることが証明できる．

4 3
1 2 3 4 5 6
10 10 10 20 20 20
10 11 12 13 14 15
60 0 60 0 60 0
2 2
0 0 0 0 0 0
60 60 60 60 60 60
8 6
58 43 60 42 53 37
13 41 55 4 21 50
35 13 54 43 24 5
40 60 57 48 60 32
51 32 58 44 60 52
40 29 25 22 0 44
31 22 26 30 49 23
16 34 4 40 21 6
0 0

1146
129600
31878

ICPC 市の道路は，市役所を中心に東西・南北に一直線の道路が等間隔に並んだ碁盤目状になっている． 道路には通し番号が振られている． 南北方向の道路の番号は次のように振られている． 市役所のある交差点を通るのが南北 0 号，それより東を通る道路は西から順に南北 1 号，南北 2 号，…，西を通る道路は東から順に南北−1 号，南北−2 号，… である． 東西方向の道路も同様で，市役所のある交差点を通る道路が東西 0 号，それより北を通る道路は南から順に東西 1 号，東西 2 号，…，南を通る道路は北から順に東西−1 号，東西−2 号，… となっている． 以下，南北 x 号と東西 y 号の交差点を交差点 (x, y) と呼ぶ． 2 つの交差点 (a, b) と (c, d) の間の移動には，両者間のマンハッタン距離 |a−c|+|b−d| に比例する時間がかかる．

東西・南北の道路はそれぞれ 10 本ごとに大通りとなっている． すなわち x が 10 の倍数の南北 x 号は大通りである． 同様に y が 10 の倍数の東西 y 号は大通りである． ICPC 市にはいくつかのランドマークがあるが，それらはすべて大通り同士の交差点にある．

市当局はいくつかのバス便を計画している． すべてのバス便は 2 つのランドマーク間を結ぶ直行便とする予定である． 各ランドマークについて，その近辺の交差点にバス停を 1 つ設置する． バス停は交差点になくてはならないが，大通り沿いである必要はない． すなわちバス停を設置する交差点 (x, y) の x, y は整数だが，10 の倍数でなくても良い． バス停とランドマークの間のマンハッタン距離は，ランドマークごとに決められた上限値以下でなければならない． この上限値は 10 の倍数である． 異なるランドマークのためのバス停を同じ交差点に設置しても構わない．

バス便が結ぶバス停間のマンハッタン距離の総和を最小化するようにバス停の設置場所を決めよ．

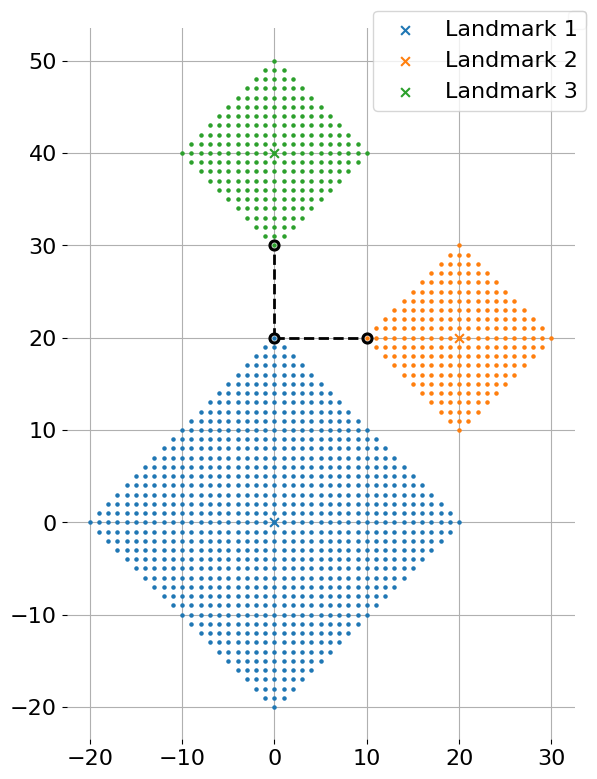
図 H-1 に Sample Input の最初のデータセットとその最適解を示す． 図中のバツ印がランドマークのある交差点を，各ドットがバス停を設置可能な交差点を表す． 丸印の付けられた交差点にバス停を設置するのが最適である．

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n m
x₁ y₁ r₁
 ⋮
x_n y_n r_n
u₁ v₁
 ⋮
u_m v_m

ここで n はランドマークの数を表し，2 ≤ n ≤ 100 を満たす． m はバス便の数を表し，1 ≤ m ≤ n(n−1)/2 を満たす． 続く n 行のうちの i 行目はランドマーク i の位置 (x_i, y_i) と，そこから対応するバス停までのマンハッタン距離の上限値 r_i を与える． ここで x_i, y_i は −10⁹ 以上 10⁹ 以下の 10 の倍数である． また r_i は 0 以上 10⁹ 以下の 10 の倍数である． 最後の m 行はバス便の一覧である． その j 行目の整数 u_j と v_j (1 ≤ u_j < v_j ≤ n) はランドマーク u_j とランドマーク v_j の間にバス便を予定していることを表す． 同じバス停の組は高々 1 度しか現れない．

入力の終わりは，2 つのゼロからなる行で表される． 入力に含まれるデータセットは 50 個以内である．

各データセットについて，バス便が結ぶバス停間のマンハッタン距離の総和の最小値を 1 行に出力せよ．

3 2
0 0 20
20 20 10
0 40 10
1 2
1 3
4 6
0 0 10
0 10 10
10 0 10
10 10 10
1 2
1 3
1 4
2 3
2 4
3 4
4 3
0 0 50
-40 0 10
40 0 10
0 -40 10
1 2
1 3
1 4
0 0

20
0
90