Links
Problem A
Marbles Tell Your Lucky Number

You can find your lucky number of the day in the following way.
Prepare four bowls and plenty of marbles. Line up the bowls from left to right, and, after deep meditation, put some arbitrary numbers of marbles in the bowls. Numbers of marbles in the bowls may vary; some bowls may be empty, but at least one of them should be non-empty.
Among non-empty bowls, choose one with the least number of marbles in it. If more than one bowl has the least number of marbles, choose the leftmost. From all the other non-empty bowls, remove the same number of marbles as in the chosen bowl. The marbles in the chosen bowl are left there.
This procedure should be repeated until only one non-empty bowl remains. The number of marbles in the non-empty bowl is your lucky number today.
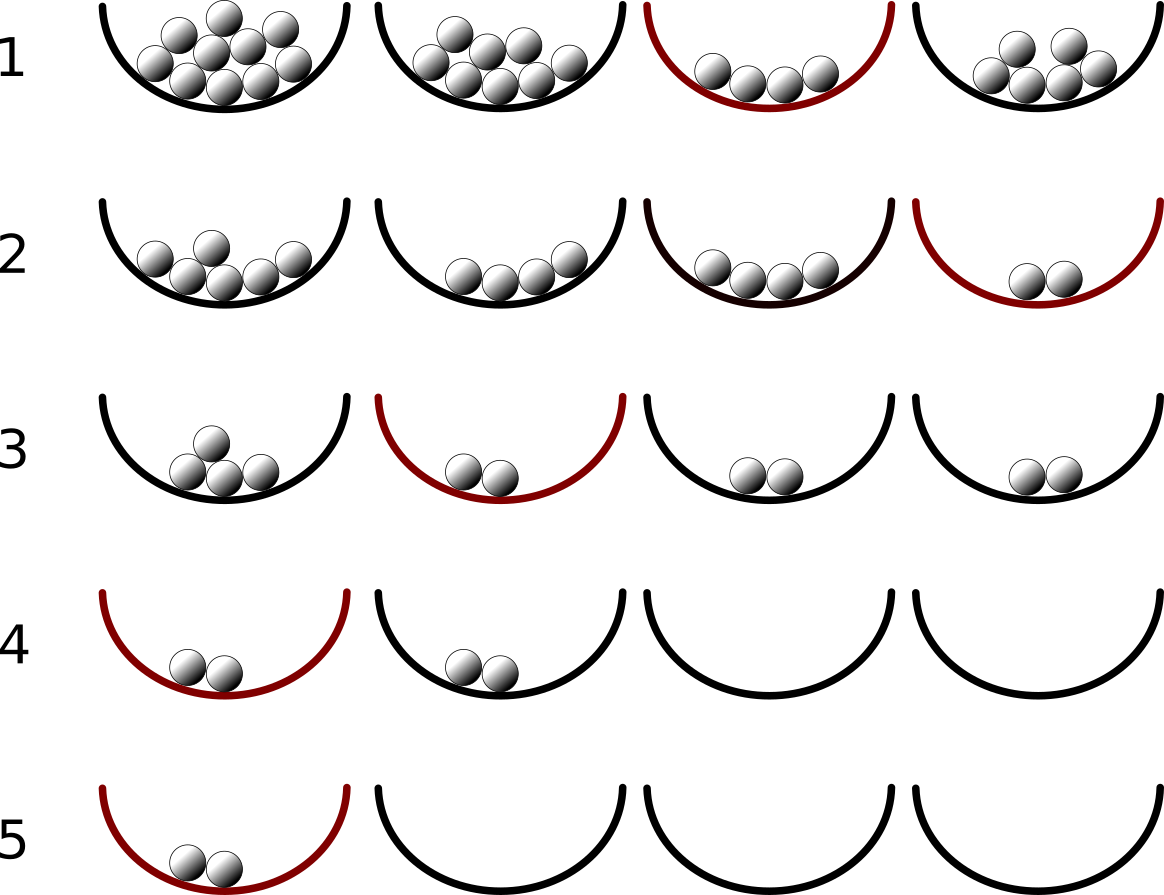
The figure to the right shows an example corresponding to the first dataset of the Sample Input.
- The bowl second from the right contains the least number of marbles, four.
- Four marbles each have been taken out from other bowls. Now the rightmost bowl has two marbles, which are the least.
- Two marbles each have been taken out from other bowls. Three bowls except the leftmost have two marbles, which are the least. The leftmost bowl of the three, that is, the second from the left, is chosen.
- Two marbles each have been taken out from other bowls. Now only two bowls have marbles in them and both have two marbles. Thus, the leftmost bowl is chosen.
- Two marbles from the second bowl have been taken out, leaving only one bowl non-empty, which is the leftmost bowl with two marbles. Yes, your lucky number of the day is two!
Input
The input consists of multiple datasets, each in the following format.
a1 a2 a3 a4
Each of the datasets consists of one line containing four integers, a1 through a4. These four integers are the numbers of marbles initially in the four bowls. All of these four integers are between 0 and 100, inclusive, and at least one of them is non-zero.
The end of the input is indicated by a line containing four zeros.
The number of datasets does not exceed 100.
Output
For each of the datasets, output the lucky number decided by the procedure described above in a line.
Sample Input
10 8 4 6 0 21 7 35 5 45 13 3 52 13 91 78 0 0 0 0
Output for the Sample Input
2 7 1 13
Problem B
Hundred-Cell Calculation Puzzles
The hundred-cell calculation is a kind of calculation training. In hundred-cell calculation, a sheet with ten by ten empty cells is given. Numbers, 0 through 9, are written on the top of the ten columns in an arbitrary order. 0 through 9 are also written at the left of the ten rows in an arbitrary order. You are to fill the empty cells with the sums of the top and left numbers, as an example shown in the figure below.
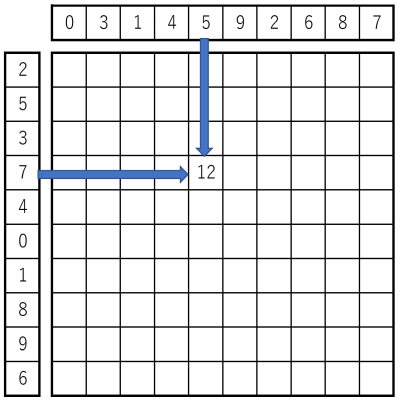
You may think of more generalized drills. Such a drill has different numbers of the columns and rows, say w × h. The numbers to be written on the top and the left can be any integers.
Hideo is designing a puzzle based on the generalized hundred-cell calculation. A sheet is given in which some of answer cells are filled with numbers, but numbers on the top and the left are omitted. The puzzle is to find these omitted numbers consistent with the filled numbers.
Hideo decided to construct puzzles by preparing sheets filled with all the correct sums and then removing some of these sums. This guarantees that the puzzle has at least one solution. The existence of the solution, however, is not enough; it should be unique.
Hideo has found through many trials that, when the leftmost of the numbers on the top is fixed to be 0, puzzles with w × h cells may have a unique solution when w + h − 1 sums are kept. He, however, could not figure out which cells to keep for a single unique solution.
Your task is to help Hideo by writing a program that judges solution uniqueness for each of the puzzle candidates he has made.
Input
The input consists of at most 100 datasets, each in the following format.
w h
x1 y1 n1
...
xk yk nk
w and h in the first line are the numbers of answer cells in one row and in one column, respectively (2 ≤ w ≤ 100 and 2 ≤ h ≤ 100). There remain k numbers (k = w + h − 1) in the answer cells. The k lines starting from the second show that the number ni is in the cell xi-th from the left and yi-th from the top. xi, yi, ni are integers satisfying 1 ≤ xi ≤ w, 1 ≤ yi ≤ h, and −100 ≤ ni ≤ 100. Here, x = 1 means the leftmost and y = 1 means the topmost. Either of xi ≠ xj or yi ≠ yj holds for different i and j.
The end of the input is indicated by a line containing two zeros separated by a space.
Output
For each dataset, output YES if the puzzle has a unique solution, and NO otherwise, in a line.
Sample Input
2 2 1 1 10 1 2 1 2 2 5 3 3 1 1 1 1 2 2 2 2 3 2 3 4 3 3 5 3 3 1 1 1 1 3 3 2 2 3 3 1 3 3 3 5 3 2 1 1 8 1 2 7 2 1 7 3 2 5 6 6 1 1 -2 1 4 4 2 2 2 3 3 3 3 4 8 4 2 -4 4 6 1 5 5 4 5 6 5 6 1 -7 6 3 -6 6 6 1 2 3 1 4 0 2 1 -3 2 3 -1 3 1 0 3 2 6 4 6 0 5 4 -5 5 5 -10 6 3 -6 6 5 -10 6 6 1 5 -2 2 5 -1 3 5 -7 4 1 5 4 2 -1 4 3 4 4 4 3 4 5 -1 4 6 2 5 5 -6 6 5 0 2 6 1 1 -2 1 2 -1 1 3 -3 1 4 -2 1 5 -5 1 6 -2 2 4 0 0 0
Output for the Sample Input
YES YES NO YES NO NO YES YES
Problem C
Tree Transformation Puzzle
Let's get started with a puzzle!
First, you are given an arithmetic expression, which solely consists of integers, operator symbols + and −, and parentheses.
(4−1)−(2+3)−(5+6) is an example of such an expression.
As is well known, the structure of an arithmetic expression is naturally represented as a tree.
For instance, the tree in Figure C-1 represents (4−1)−(2+3)−(5+6).
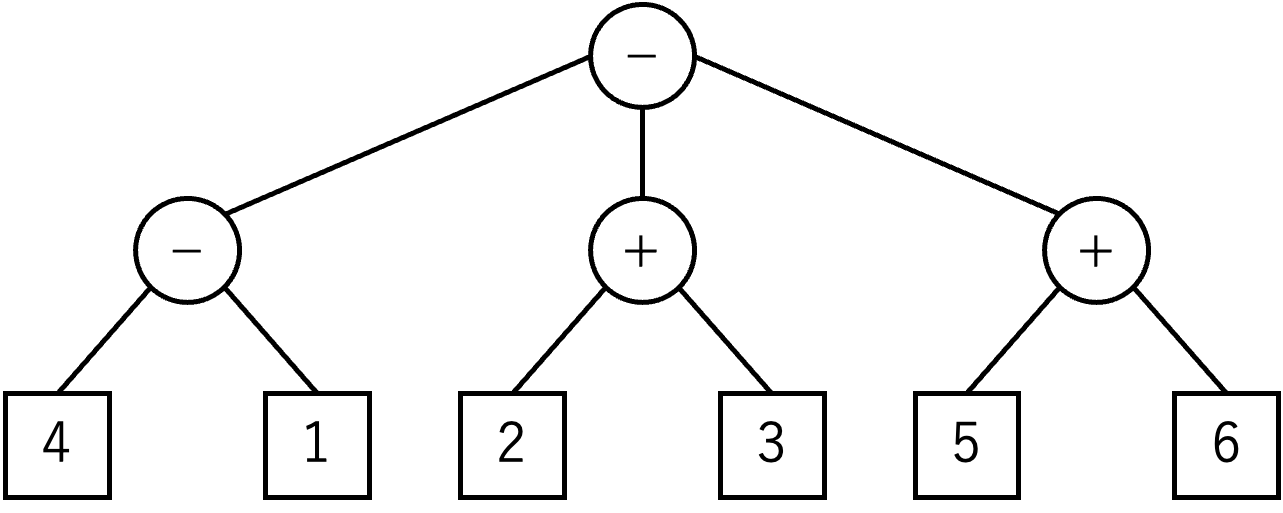
Figure C-1: A tree representation of
(4−1)−(2+3)−(5+6)
In the tree of the figure, each box is a leaf node labeled with an integer, and each circle is a non-leaf node labeled with an operator symbol + or −.
The value of a leaf node labeled with an integer is that integer.
The value of a node with an operator symbol +
is the sum of the values of all of its child nodes.
The value of a node with an operator symbol −
is the value of its leftmost child node subtracted with the values of all the other child nodes.
The value of the root node calculated in this manner is equal to the value of the given expression calculated with
the usual rules of arithmetic, of course.
For any trees representing arithmetic expressions given for this puzzle, the root nodes have three child nodes, and all the other non-leaf nodes have one parent and two child nodes. Therefore, every non-leaf node is directly connected to exactly three nodes.
Let us think of transformation of the tree structure corresponding to the given arithmetic expression by applying either of the following operations on the entire tree or any of its subtrees arbitrarily many times.
- Swapping two child nodes of a non-leaf node.
- For the leftmost (or the rightmost) child node of the root, if it is a non-leaf, making it the new root of the tree and the old root node the rightmost (or the leftmost, respectively) child node of the new root.
Unless explicitly stated above, these operations change neither the parent-child relationship between two nodes nor the left-to-right order among child nodes sharing the same parent.
The new tree resulted from such operations represents a possibly different arithmetic expression having a possibly different value. The goal of this puzzle is to find the maximum possible value of such an expression through the operations described above applied arbitrarily many times.
For example, by swapping the two child nodes of the leftmost non-leaf node in Figure C-1, which has an operator symbol −, you will have the tree in Figure C-2.
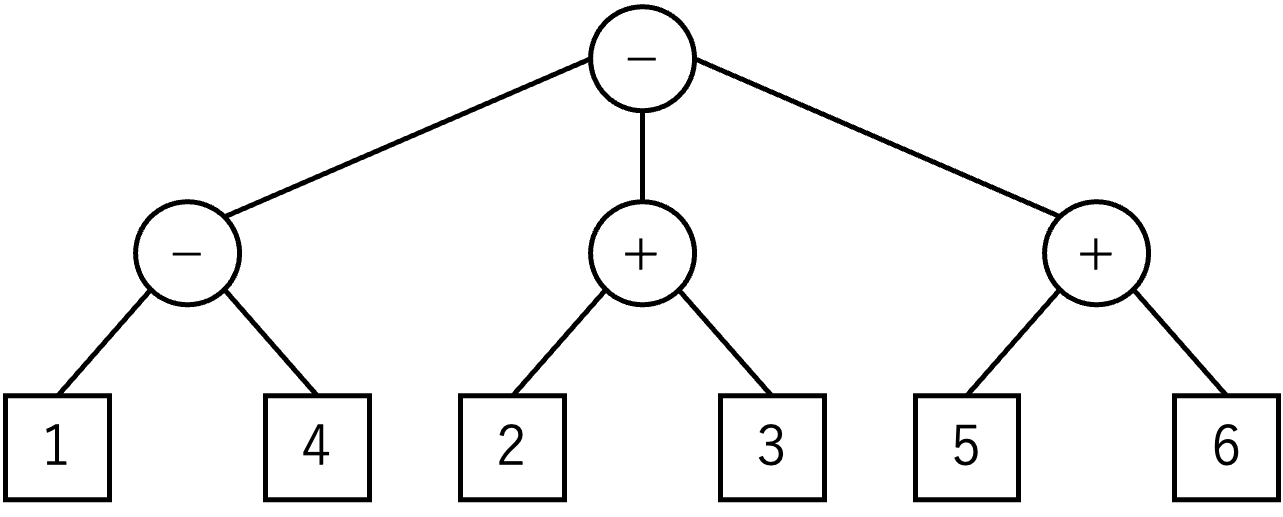
Figure C-2: The result of swapping the two leftmost leaf nodes
And then by swapping the leftmost and the rightmost child nodes of the root in Figure C-2, you will have the tree in Figure C-3.
The value of the original arithmetic expression (4−1)−(2+3)−(5+6) is −13, and those of the expressions represented by the two trees in Figures C-2 and C-3 are −19 and 9, respectively.
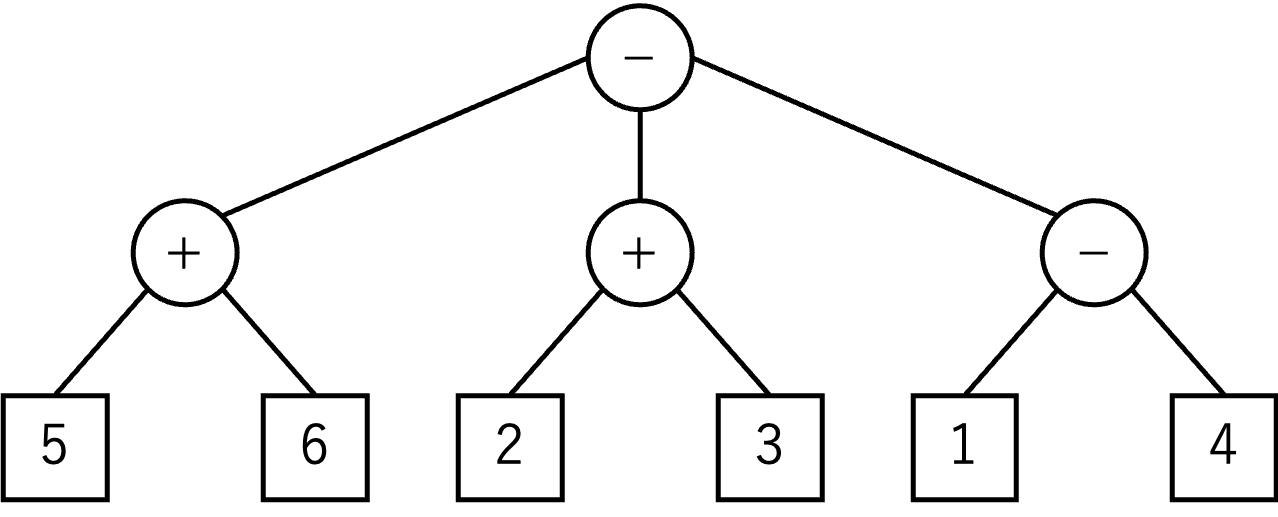
Figure C-3: The result of swapping the leftmost and the rightmost nodes of the root
In addition, by making the leftmost child node of the root in Figure C-3 the new root, and the original root the rightmost child node of the new root, you will have the tree in Figure C-4.
The expression represented by this tree is 5+6+((2+3)−(1−4)) and its value is 19, which is the maximum value that can be taken in this case.
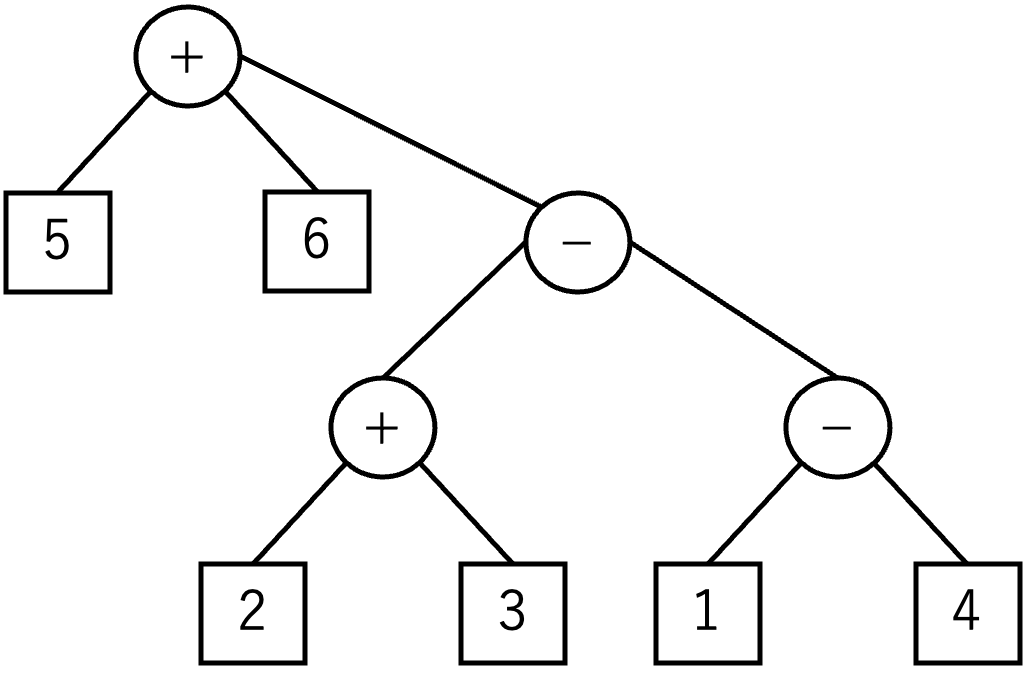
Figure C-4: The result of making the leftmost non-leaf node the new root
Input
The input consists of multiple datasets, each being a line containing a root-expression defined in the following.
- A root-expression is a character string that consists of three occurrences of non-root-expressions and either two plus (
+) or two minus (−) signs delimiting the non-root-expressions. - A non-root-expression is a single digit, denoting a single digit integer, or a character string consisting of two occurrences of non-root-expressions, a plus or minus sign delimiting them, and an open and a close parentheses enclosing them.
Each dataset has at lease five characters (i.e. three digits and two signs). The total number of the characters in all the datasets in the input is at most 500,000. The depths of nested parentheses are no greater than 100.
The end of the input is indicated by a line containing a minus one (−1).
Output
For each dataset, output one line containing the answer of the puzzle.
Sample Input
2+3+4 2-3-4 ((5-1)-1)-7-9 (3+2)-(4-1)-(5+6) -1
Output for the Sample Input
9 -1 7 19
Problem D
Handing out Balloons
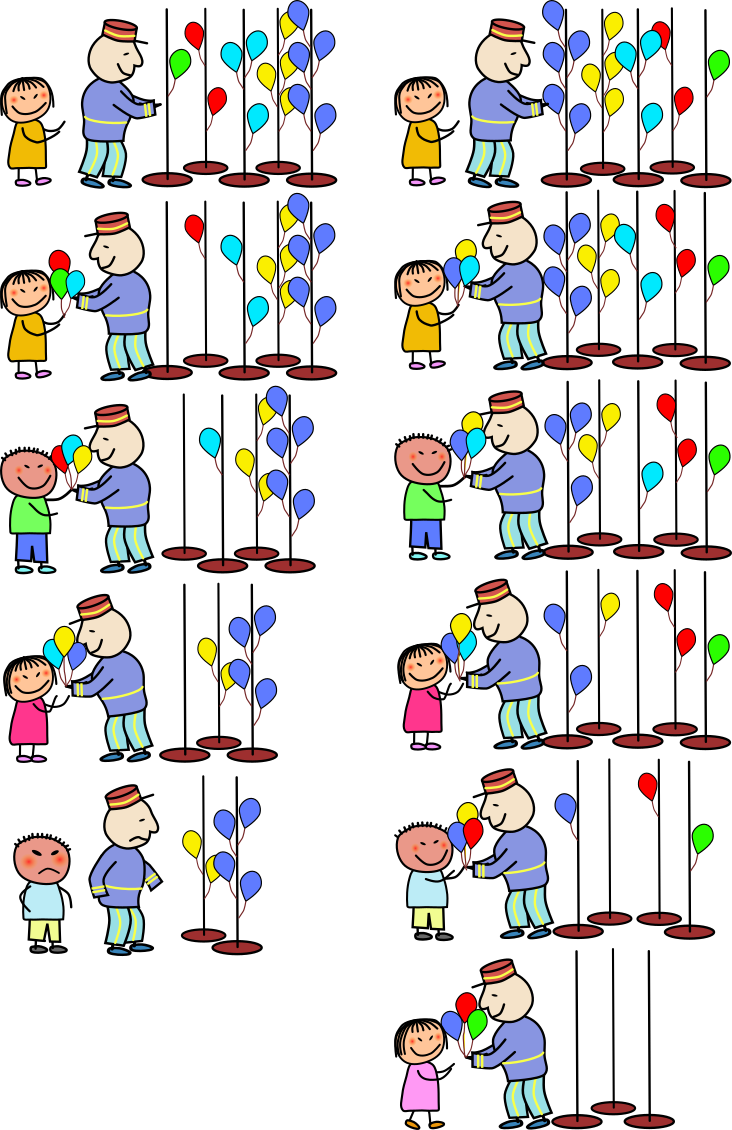
Each time an ICPC participant team has successfully solved a problem at the competition site, a balloon of a color specific to that problem is delivered to that team. You had thus prepared enough number of balloons of various colors for the case when all the teams solved all the problems, but many problems have been solved by few teams. You thus decided to give away the remaining balloons to the kids in the neighborhood.
You are preparing poles, each tied down with one or more balloons of the same color. You are lining up these poles from left to right. Whenever a kid comes up, you give three balloons of different colors to the kid picking up one from each of the three leftmost poles. Poles that run out of the balloons are removed, and when the poles remaining are two or less, you finish giving balloons away.
The number of kids you can give the balloons depends on the order of the poles. Find the maximum possible number of kids you can give the balloons by arranging the order of poles appropriately.
The figure on the right depicts the consequences of different arrangements of five poles with 1, 2, 3, 4 and 5 balloons. When poles are lined up in the order of 1, 2, 3, 4 and 5 balloons, you can give to only three kids; when they are in the order of 5, 4, 3, 2 and 1 balloons, you can give to five kids.
Input
The input consists of multiple datasets, each in the following format.
n
b1 b2 … bn
n is the number of poles. n is an integer between 3 and 50, inclusive. b1 through bn are the numbers of the balloons on the poles. Each bi is a positive integer not exceeding 50.
The end of the input is indicated by a line containing a zero. The number of datasets does not exceed 50.
Output
For each dataset, output a single line containing the maximum number of kids you can give the balloons to.
Sample Input
5 1 2 3 4 5 9 1 3 3 3 3 3 3 4 4 4 5 2 8 3 0
Output for the Sample Input
5 9 5
Problem E
Time is Money
The city of ICPC has made excessive pedestrian separation, making transportation in the city quite complicated. Citizens of the ICPC city thus have big concern on efficient transportation to save time. The residents are eager to reach their destinations as fast as possible by repeating taxi rides on driveways and walks on footpaths.
Many cabstands are in the city. Footpaths and/or driveways directly connect some of the cabstand pairs allowing both-way traffic. Some pairs of cabstands may have no direct nor indirect paths.
When you are on foot at a cabstand, you can either
- Walk a footpath, if any, to another cabstand, or
- Pick up a taxi, if any driveway connects the cabstand.
When you are on a taxi, you can either
- Keep riding to another cabstand via a driveway, or
- Get out of the taxi.
You can get out of a taxi only at cabstands.
Transportation on a footpath or a driveway takes time defined for each of the roads. In addition, you have to wait one minute to pick up a taxi for the first time. The waiting time is doubled for each subsequent taxi picks, that is, two minutes for the second time, four minutes for the third time, and 299 minutes for the 100-th time.
You are initially at one of the cabstands on foot. Find the shortest time possible to reach the destination cabstand.
Input
The input consists of multiple datasets, each in the following format.
n p q
a1 b1 c1
…
ap bp cp
d1 e1 f1
…
dq eq fq
Here, n, p, and q are the numbers of cabstands, footpaths, and driveways, respectively. n is an integer between 2 and 20000, inclusive. Cabstands are numbered 1 through n. p and q are positive integers not exceeding 20000. ai, bi, and ci describe the i-th footpath, meaning that it connects the cabstands numbered ai and bi, and it takes ci minutes to walk. dj, ej, and fj describe the j-th driveway, meaning that it connects the cabstands numbered dj and ej, and it takes a ride of fj minutes. ai, bi, dj, and ej are positive integers not exceeding n. ci and fj are positive integers not exceeding 106.
The end of the input is indicated by a line containing three zeros. The total of n, the total of p, and the total of q of all the datasets do not exceed 200000, respectively.
Output
For each dataset, output a single line containing the shortest time required in minutes for transporting from the cabstand number 1 to the cabstand number n modulo 109+7. If such transportation is impossible, output −1 instead.
Sample Input
5 4 2 1 2 1 2 3 100 3 4 1 4 5 100 2 3 10 4 5 10 4 1 1 1 2 100 2 3 100 4 3 3 1 2 10 2 3 1 3 4 10 2 1 2 3 2 2 4 3 2 0 0 0
Output for the Sample Input
25 -1 7
Problem F
Princess' Perfectionism
The princess has n spies, and she is planning to assign exactly n tasks to them. Skills of the spies constrain the eligibilities for the tasks. The princess is a perfectionist, and she is not satisfied unless
- each spy is assigned exactly one task, and
- each task is assigned to exactly one spy.
Fortunately, this turned out to be feasible; there may be, however, selfish spies who cling to specific tasks among those eligible for themselves. She plans to train some of the spies so that a satisfiable task assignment is possible even when any single spy is selfish. One session trains a spy so that he/she becomes eligible for a new task. She wants to minimize the number of training sessions.
Your mission is to suggest an optimal training plan to the princess. You are given all the eligible pairs of a spy and a task. If no spy is selfish, the tasks can be assigned to the spies so that the princess is satisfied. The eligible pairs should be augmented through training so that an assignment that satisfies the princess always exists even if any single spy clings to a task that is eligible for him/her. Spies may cling to a task newly made eligible through training. Note that no training at all might be required for the purpose.
Input
The input consists of multiple datasets, each in the following format.
n m
s1 t1
...
sm tm
- n is the number of spies as well as the number of tasks. n is a positive integer not exceeding 2000.
- m is the number of eligible pairs of a spy and a task. m is a positive integer not exceeding 105.
- The spies and tasks are respectively represented by integers between 1 and n.
- For i = 1, 2, ..., m, (si, ti) is an eligible pair, which represents that the spy si is eligible for the task ti. In addition, if i ≠ j, then si ≠ sj or ti ≠ tj.
- It is guaranteed that there exists a subset of eligible pairs in which all spies and tasks appear exactly once, that is, the princess can be satisfied by some assignment if no spy is selfish.
The end of the input is indicated by a line containing two zeros with a space between them. The number of datasets in the input is at most 25.
Output
For each dataset, output a nonnegative integer k in the first line, and in each of the next k lines, output two integers xi and yi (i = 1, 2, ..., k) with a space between them. k is the minimum number of pairs of a spy and a task to be trained, and {(x1, y1), (x2, y2), ..., (xk, yk)} is a set of pairs that attains the minimum, where xi and yi represent a spy and a task, respectively. There may be two or more sets of pairs to be trained with the least number of elements; any of them shall be deemed correct.
Sample Input
2 3 1 1 1 2 2 2 2 2 1 1 2 2 4 7 1 1 1 2 2 2 3 2 3 3 3 4 4 4 5 10 1 1 1 2 1 3 2 1 2 2 2 4 3 3 4 4 4 5 5 5 0 0
Output for the Sample Input
1 2 1 0 2 2 3 4 1 2 3 2 5 3
Problem G
Positioning the Lights
You are given a map of a dungeon consisting of a number of aligned squares forming a rectangle. Each square is either a wall or an empty square. The dungeon has no open space. More specifically, it satisfies the following two conditions.
- No block of 2 × 2 or larger empty squares is in the dungeon.
- Three or more empty squares are not diagonally aligned consecutively.
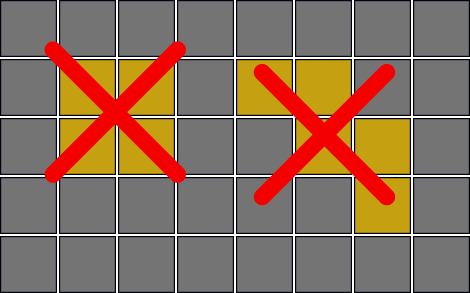
You have many lights. When you place a light on an empty square, it brightens that square and all the consecutive empty squares, if any, in the four directions, up, down, left and right. You can place at most one light in each empty square, and you can place the lights in as many squares as you want.
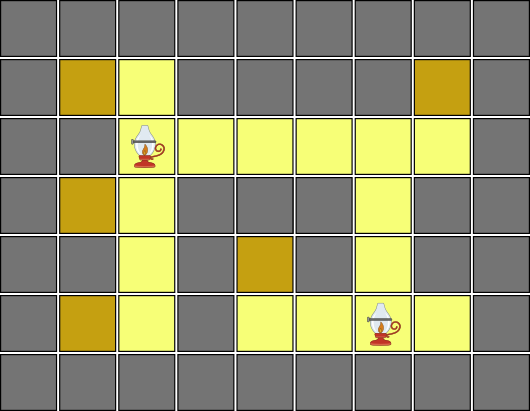
Compute the number of possible combinations of light placements that brighten all the empty squares.
Input
The input consists of multiple datasets, each in the following format.
n m
c1,1 ... c1,m
...
cn,1 ... cn,m
n and m represent the number of squares in the vertical and horizontal directions, respectively, and satisfy 1 ≤ n ≤ 30 and 1 ≤ m ≤ 30. Each of ci,j is a character '#' or '.'. If it is '#', the square at the position i from the top and j from the left is a wall; if it is '.', the square is empty.
The end of the input is indicated by a line containing two zeros. The number of datasets does not exceed 50.
Output
For each dataset, output the number of possible combinations of light placements that brighten all the empty squares, modulo 109+7 in a single line.
Sample Input
2 2 .# #. 3 3 ... .#. ... 2 3 #.. ..# 3 3 #.# ... #.# 3 5 .#.#. ..... #.#.# 0 0
Output for the Sample Input
1 161 9 25 243
Problem H
Ninja Escape
I've just completed a mission inside ICPC Castle in the enemy country, and am leaving the castle through the underground escape route dug in advance. However, there are n watchtowers placed at equal intervals in the castle, and I must reach the entrance of the escape route without being noticed by the guards in the watchtowers.
The yard of the castle has a rectangular shape of 100n × 100. Let the coordinates of the back left corner be (0, 0) and the coordinates of the front right corner be (100n, 100). The watchtowers are numbered from 1 to n, and the k-th watchtower is located at the coordinates (100k − 50, 50).
I am currently at the coordinates (x1, y1), and I want to move to the coordinates (x2, y2), where the entrance of the escape route is located, in the shortest possible time.
Should I move too fast near a watchtower, the guards might notice the footsteps. Strictly saying, I must not move faster than D2 per second, where D is the distance to the nearest watchtower.
I'm wondering how long it takes to reach the entrance of the escape route.
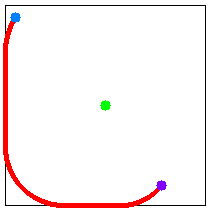
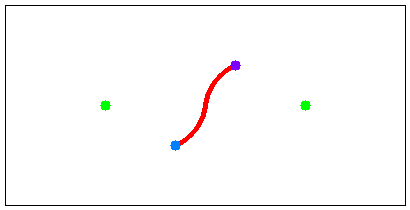
For example, when there is one watchtower and the coordinates of the starting location (current location) and the goal location (the entrance of the escape route) are (5, 6) and (78, 90), respectively, the optimal route is as shown in Figure H-1. For another example, when there are two watchtowers and the coordinates of the starting location and the goal location are (85, 70) and (115, 30), respectively, the optimal route is as shown in Figure H-2. These are corresponding to the first two datasets in the Sample Input.
 |
 |
|
|
|
Input
The input consists of multiple datasets, each in the following format.
n x1 y1 x2 y2
n is the number of watchtowers. n is a positive integer not exceeding 107. (x1, y1) gives the coordinates of the starting location, and (x2, y2) gives the coordinates of the goal location. x1 and x2 are integers between 0 and 100n, inclusive. y1 and y2 are integers between 0 and 100, inclusive. The coordinates of the starting and goal locations are different. The coordinates of the starting and goal locations are also different from those of any watchtowers.
The end of the input is indicated by a line containing five zeros. The number of datasets in the input is at most 1000.
Output
For each dataset, output the shortest possible time to move in seconds. The error contained in the output should not exceed 10−8. The output shall be deemed correct if its relative error or its absolute error is within this limit.
Sample Input
1 5 6 78 90 2 85 70 115 30 1 2 50 98 50 1 12 23 34 45 1 23 45 67 89 2 80 50 195 50 2 80 50 180 70 2 10 50 190 60 10 1 2 987 65 10 80 60 920 40 10 50 90 950 10 0 0 0 0 0
Output for the Sample Input
0.056924948365 0.024806946918 0.060137708723 0.039815727511 0.054616382922 0.070423053859 0.063218824369 0.091771006495 0.338081602957 0.297714980979 0.316557291903
