Links
Problem A
ビー玉占い

今日のラッキーナンバーを見つけよう.
椀を四つとビー玉をたくさん用意する. 椀を横一列に並べ、深く瞑想してから,それぞれの椀にいくつかのビー玉を入れる. ビー玉の個数はばらばらでよく, 空の椀があってもよいが,少なくとも一つは空でないようにする.
空でない椀のうちでビー玉が一番少ないものを選ぶ. 一番少ない同数の椀が二つ以上あるときは,一番左の椀を選ぶ. 選んだ以外の空でないすべての椀から、 選んだ椀のビー玉と同数のビー玉を取り除く. 選んだ椀の中のビー玉はそのままにしておく.
この手続きを空でない椀が一つだけになるまで繰り返す. その椀に残ったビー玉の個数があなたの今日のラッキーナンバーだ.
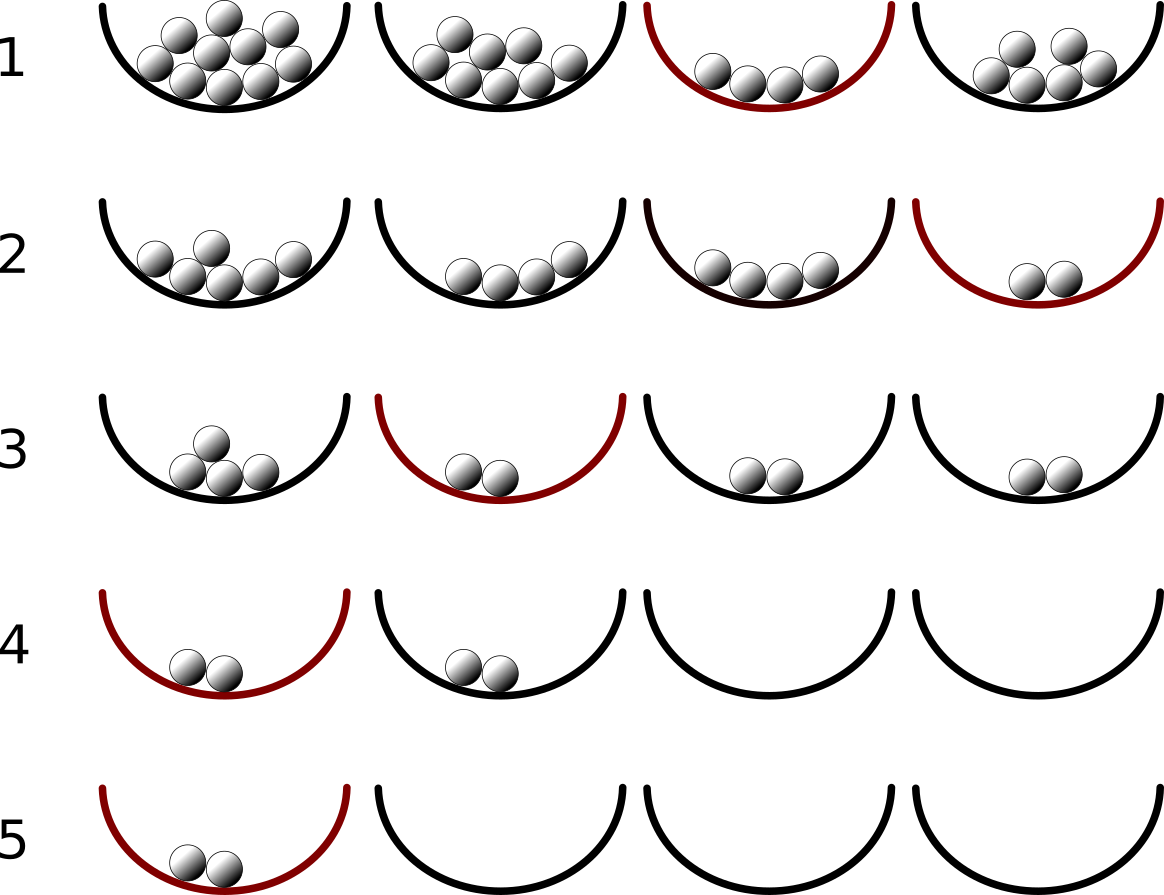
右図に Sample Input の最初のデータセットに対応する例を示す.
- 右から二番目の椀のビー玉の個数が最少の 4 個である.
- 他の各椀からビー玉を 4 個ずつ取り除くと, 一番右の椀に残るビー玉 2 個が最少になる.
- 他の各椀からビー玉を 2 個ずつ取り除くと, 一番左以外の三つの椀すべてに 2 個のビー玉が残り, これが最少である. その三つの中で最も左にあるのは全体の左から二つ目の椀なので,それを選ぶ.
- 他の各椀からビー玉を 2 個ずつ取り除くと, これでビー玉が残る椀は二つだけで,両方共 2 個になる. そこで一番左の椀を選ぶ.
- 二番目の椀からビー玉 2 個を取り除くと, 空でないのは一番左の椀だけになり,その中のビー玉は 2 個である. そう,あなたの今日のラッキーナンバーは 2 だ!
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
a1 a2 a3 a4
各データセットは a1 から a4 の 4 整数を含む 1 行からなる. これらの 4 整数は四つの椀に最初に入れるビー玉の個数を意味し, いずれも 0 以上 100 以下で,少なくとも一つは 0 でない.
入力の終わりは四つのゼロを含む行で示す.
データセットは 100 個以内である.
Output
各データセットに対して, 上述の手順で求めたラッキーナンバーを 1 行に出力せよ.
Sample Input
10 8 4 6 0 21 7 35 5 45 13 3 52 13 91 78 0 0 0 0
Output for the Sample Input
2 7 1 13
Problem B
百ます計算パズル
百ます計算は計算練習の一種である. 百ます計算では 10 × 10 の空きマスがある紙を用いる. 各列の上端には 0 から 9 までの数が順不同に書いてあり, 各行の左端にも 0 から 9 までの数が順不同に書いてある. 空きマスには下図の例のように上端と左端の数の和を書き込んでいく.
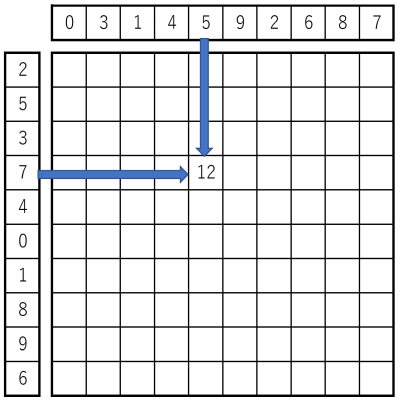
より一般化した問題を考えることもできる. そのような問題では,列や行の数を例えば w × h に変えることができる. また,各列の上と各行の左に書かれた数は,任意の整数とすることもできる.
英男君は,この一般化した百ます計算を題材にしてパズルを作っている. そのパズルでは,解答マスのいくつかに数が入っているが, 上端や左端の数は書いていない. パズルは解答マスに入っている数に矛盾しない上端・左端の数を見つける,というものだ.
英男君は解答マスがすべて正しい和で埋まっている紙を用意して, その解答マスの中の和をいくつか消していくことでパズル問題を作ることにした. こうすればパズルの解は少なくとも 1 つ存在することが保証できる. しかし解は存在するだけでは不十分で,一意であるようにしたい.
いろいろとやってみると,上端の数の一番左を 0 と決めておくとき, 横 w × 縦 h の解答マスのうち, w + h − 1 個のマスの値を残すと, 解が一意になることがあることがわかった. しかし,どのマスを残せば一意になるかはわかっていない.
英男君が作ったパズル候補のそれぞれについて, 解が一意に定まるかどうかを判定するプログラムを作って英男君を助けてあげて欲しい.
Input
入力は 100 個以下のデータセットからなる. 各データセットは次の形式で表される.
w h
x1 y1 n1
...
xk yk nk
1 行目の w は横方向,h は縦方向の解答マスの個数である (2 ≤ w ≤ 100 および 2 ≤ h ≤ 100). 解答マスには k 個 (k = w + h − 1) の数が残されている. 2 行目からの k 行は, 左から xi 番目,上から yi 番目の解答マスに ni が入っていることを表す. xi, yi, ni は,それぞれ 1 ≤ xi ≤ w, 1 ≤ yi ≤ h, −100 ≤ ni ≤ 100 を満たす整数である. ここで,xi = 1 が最も左,yi = 1 が最も上のマスである. 異なる i と j について,xi = xj かつ yi = yj であることはない.
入力の終わりは,空白で区切られた 2 つのゼロからなる行で表される.
Output
各データセットについて,パズルの解が一意に決まるならば YES,そうでなければ NO を 1 行に出力せよ.
Sample Input
2 2 1 1 10 1 2 1 2 2 5 3 3 1 1 1 1 2 2 2 2 3 2 3 4 3 3 5 3 3 1 1 1 1 3 3 2 2 3 3 1 3 3 3 5 3 2 1 1 8 1 2 7 2 1 7 3 2 5 6 6 1 1 -2 1 4 4 2 2 2 3 3 3 3 4 8 4 2 -4 4 6 1 5 5 4 5 6 5 6 1 -7 6 3 -6 6 6 1 2 3 1 4 0 2 1 -3 2 3 -1 3 1 0 3 2 6 4 6 0 5 4 -5 5 5 -10 6 3 -6 6 5 -10 6 6 1 5 -2 2 5 -1 3 5 -7 4 1 5 4 2 -1 4 3 4 4 4 3 4 5 -1 4 6 2 5 5 -6 6 5 0 2 6 1 1 -2 1 2 -1 1 3 -3 1 4 -2 1 5 -5 1 6 -2 2 4 0 0 0
Output for the Sample Input
YES YES NO YES NO NO YES YES
Problem C
木変形パズル
さあ,パズルを始めよう!
最初に,算術式が与えられる.この算術式は,整数,演算子記号 + と −,そして括弧のみから構成される.
(4−1)−(2+3)−(5+6) はこのような算術式の例である.
よく知られているように,算術式の構造は,自然に木として表すことができる.
図 C-1 中の木は (4−1)−(2+3)−(5+6) を表現するものである.
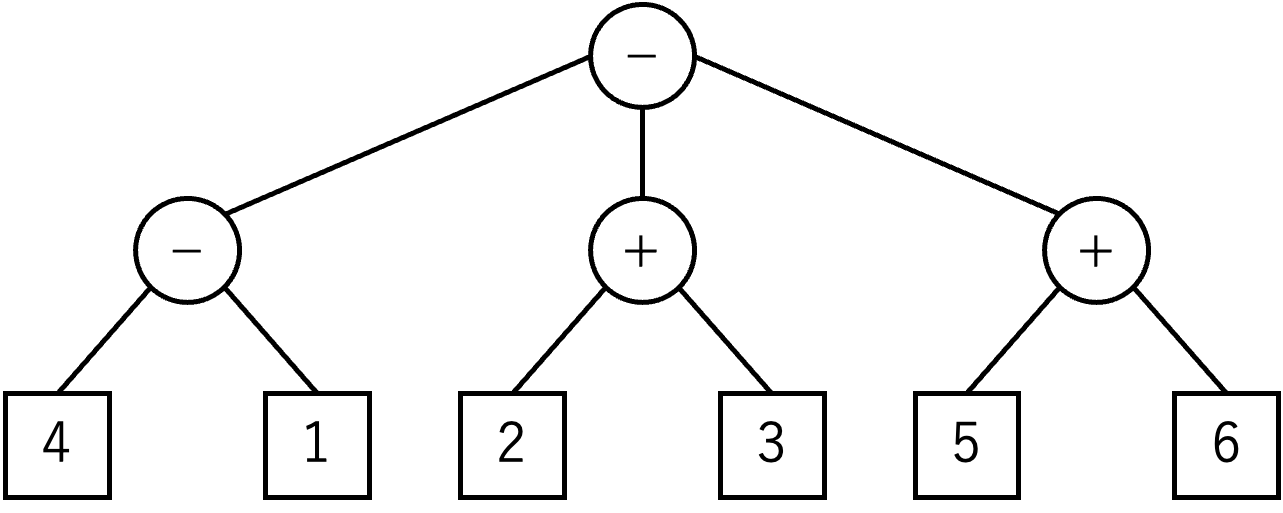
図 C-1:
(4−1)−(2+3)−(5+6) の木表現
この図の木で,各四角形は葉ノードであり,整数のラベルがついている.
また,各円は葉以外のノードであり,演算子記号 + または − のラベルがついている.
葉ノードの値はそこについているラベルの整数値そのものである.
演算子記号 + を持つノードの値は,その子ノードの値の総和である.
演算子記号 − を持つノードの値は,
その最左の子ノードの値から他の子ノードの値すべてを減じた差である.
このように計算した根ノードの値は,与えられた算術式を通常の算術の規則に従って計算した値と,もちろん一致する.
このパズルで与えられる算術式を表すあらゆる木において,根ノードは 3 つの子ノードを持ち,根でも葉でもないノードは 1 つの親ノードと 2 つの子ノードを持つ. したがって,葉以外のすべてのノードは,ちょうど 3 つのノードと直接つながっている.
与えられた式に対応する木構造を,その全体または一部に対して以下の操作を何度でも繰り返すことで,変形することを考えよう.
- 葉以外のノードの 2 つの子ノードを入れ替える.
- 根ノードの最左 (または最右) の子ノードが葉ノードでないとき,そのノードを新しい根ノードとし,古い根ノードを新しい根ノードの最右 (または最左) の子ノードとする.
上で明示的に述べられているものを除き,これらの操作は,ノード間の親子関係を変えないし,同じ親を共有する子ノード間の左右の順序も変えない.
こうした操作を施した結果の木は,元とは違う算術式を表し,元とは違う値を持つかもしれない.このパズルのゴールは,上述の操作を繰り返し適用することで得られる式の値のうちの最大値を求めることである.
たとえば,図 C-1 において,葉ノード以外で最も左のノード(−のラベルがついたもの)の2つの子ノードを入れ替えると,図 C-2 の木が得られる.
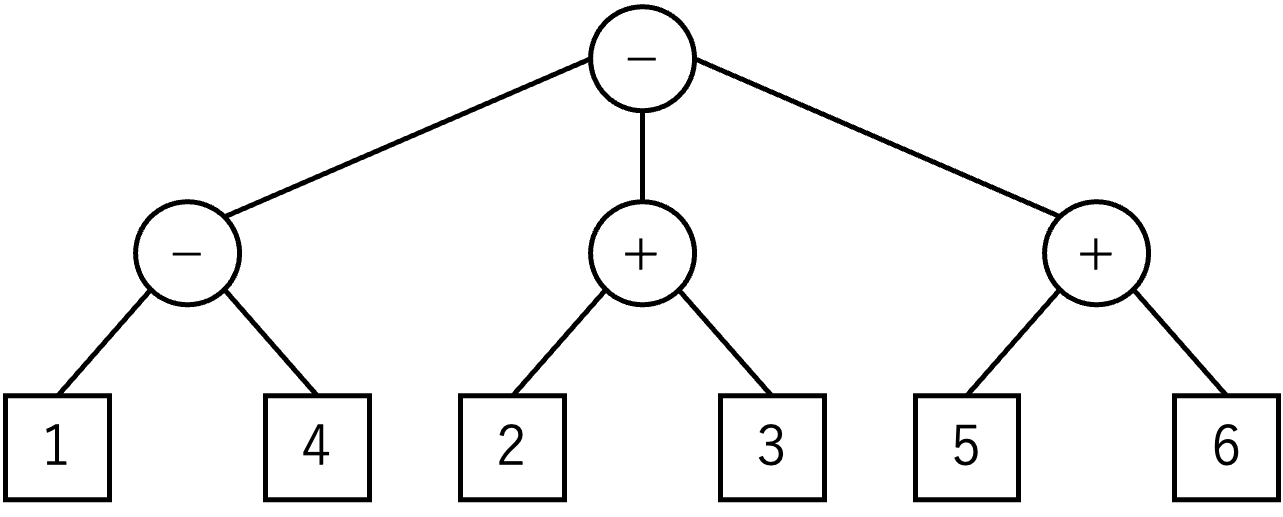
図 C-2: 一番左の 2 つの葉ノードを入れ替えた結果
ここで,図 C-2 において,根ノードの最左と最右の子ノードを入れ替えると,図 C-3 の木が得られる.
元の算術式 (4−1)−(2+3)−(5+6) の値は −13 であったが,図 C-2, C-3 の木が表す算術式の値は,それぞれ −19 と 9 になる.
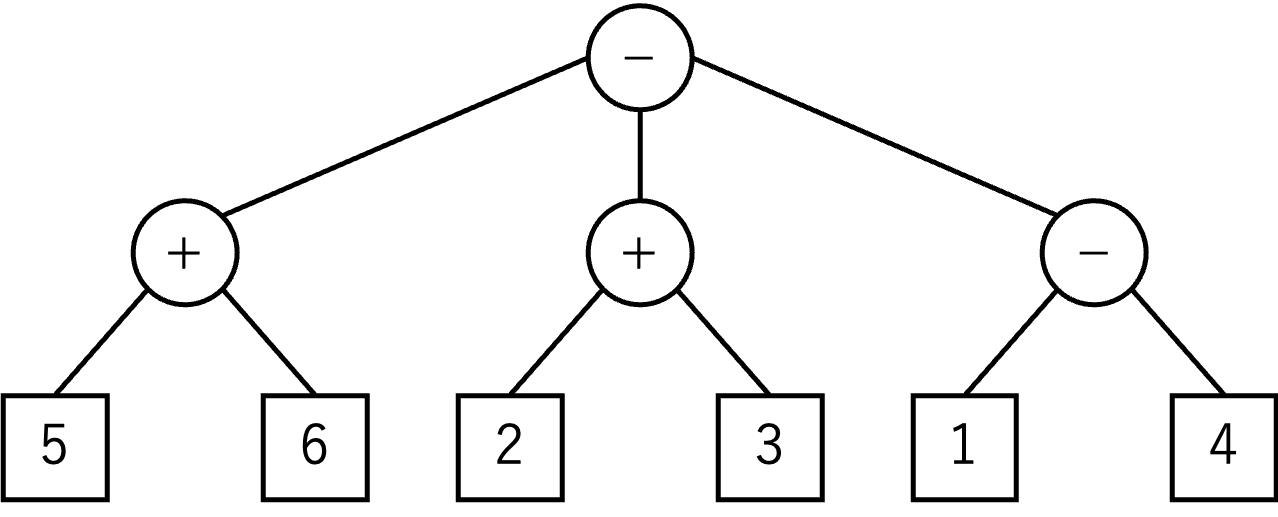
図 C-3: 根ノードの最左と最右の子ノードを入れ替えた結果
さらに,図 C-3 の根ノードの最も左の子ノードを新しい根ノードとし,元の根ノードを新しい根ノードの最も右の子ノードにすると,図 C-4 の木が得られる.
この木が表す算術式は 5+6+((2+3)−(1−4)),その値は 19 となり,これがこの例の場合に取りうる最大値である.
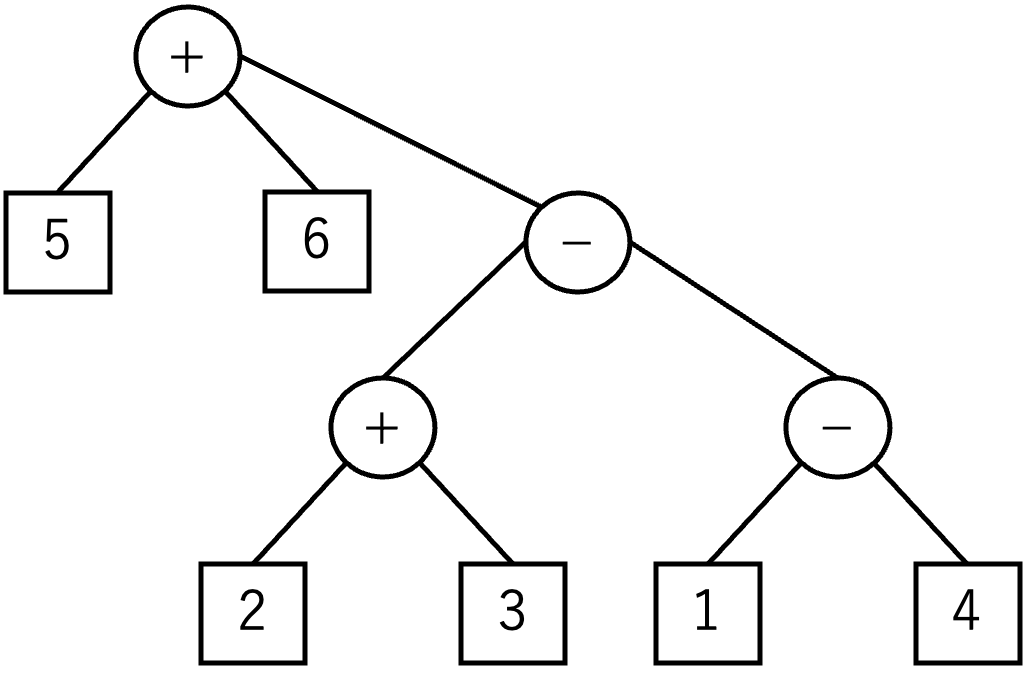
図 C-4: 葉ノード以外で最左のノードを新たな根ノードとした結果
Input
入力は複数のデータセットからなる. 各データセットは次に定義するroot式だけを含む 1 行である.
- root式は,3 個のnon-root式とこれらを区切る 2 個の加算記号 (
+) または 2 個の減算記号 (−) からなる文字列である. - non-root式は,数字 1 文字 (1 桁の整数を表す) であるか,2 個のnon-root式,これらを区切る 1 個の加算記号または減算記号,そしてこれらを囲む 1 個ずつの開き括弧と閉じ括弧からなる.
各データセットは,少なくとも 5 個の文字 (i.e. 3 個の数字と 2 個の記号) を含む. 入力の全データセットに含まれる文字数の合計は高々 500,000 である. 括弧のネストの深さが 100 を超えることはない.
入力の終わりは,−1 だけからなる行で表される.
Output
各データセットについて,パズルの答えを 1 行で出力せよ.
Sample Input
2+3+4 2-3-4 ((5-1)-1)-7-9 (3+2)-(4-1)-(5+6) -1
Output for the Sample Input
9 -1 7 19
Problem D
風船配り
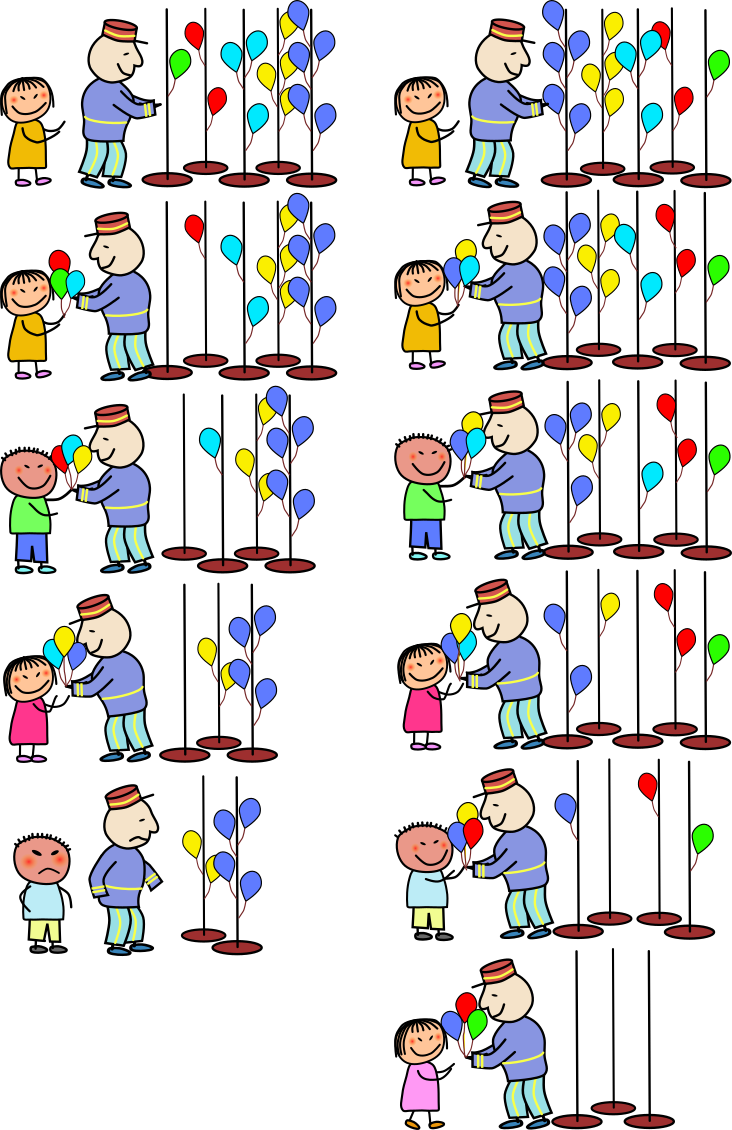
ICPC の競技会場では,参加チームが問題に正答するたびに, その問題に対応する色の風船をひとつ,そのチームに配ります. そこであなたは,さまざまな色の風船を, 全部のチームが全問正解してもいいだけの個数用意しました.しかし, 多くの問題についてはごく少数のチームしか解けませんでした. そこであなたは余った風船を近所の子供たちに配ることにしました.
同じ色の風船をいくつか結んだポールを何本か用意して,左から右に並べます. 子供が来ると,左から順に 3 本のポールからひとつずつ風船を外し,3 色の風船をあげます. 風船がなくなったポールは取り除き, 残るポールが 2 本以下になったら風船配りはおしまいです.
風船をもらえる子供の数はポールの順序によって変わります. 上手にポールを並べたら最大何人の子供が風船をもらえるでしょうか.
右の図は風船の個数が 1, 2, 3, 4, 5 のポール 5 本の並べ方を変えるとどうなるかを示しています. ポールを風船の個数が 1, 2, 3, 4, 5 の順に並べると風船をもらえる子供は 3 人だけですが, 5, 4, 3, 2, 1 の順ならば 5 人の子供がもらえます.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n
b1 b2 … bn
n はポールの本数を表す. n は,3 以上 50 以下の整数である. b1 から bn は各ポールの風船の数を表す. bi は,50 以下の正の整数である.
入力の終わりは,ひとつのゼロからなる行で表される. データセットは 50 個以内である.
Output
各データセットについて,最大で何人の子供に風船を配れるかを示す整数を 1 行で出力せよ.
Sample Input
5 1 2 3 4 5 9 1 3 3 3 3 3 3 4 4 4 5 2 8 3 0
Output for the Sample Input
5 9 5
Problem E
時は金なり
ICPC 市は歩車分離を進め過ぎたため,市内の移動が複雑で面倒になってしまった. そのため市民は移動時間を短縮することへの関心が高くなっている. 人々はタクシーに乗って車道を行くのと歩道を歩いて行くのを上手に繰り返して, できるだけ早く目的地に到着したいと考えている.
ICPC 市にはたくさんのタクシースタンドがある. いくつかのタクシースタンドの間には直接双方向に行き来できる歩道や車道がある. すべてのタクシースタンドの間に直接・間接の経路が必ずあるとは限らない.
タクシースタンドにいてタクシーに乗っていないときは,
- そこにつながる歩道があればその道を歩いて移動すること, または
- そこにつながる車道があればその場でタクシーに乗り込むこと
ができる.タクシーに乗っているときは,
- 現在乗っているタクシーのまま車道でつながっている別のスタンドに移動すること,または
- その場でタクシーを降りること
ができる. タクシースタンド以外ではタクシーを降りられない.
歩道や車道を移動するとき,その道ごとに決まった時間がかかる. また,タクシーは乗るときに待ち時間がかかる. 待ち時間は,初めてタクシーに乗るときは 1 分, 以降は直前の待ち時間の 2 倍である. つまり 2 回目に乗るときは 2 分,3 回目に乗るときは 4 分, 100 回目に乗るときは 299 分かかる.
あなたは最初タクシースタンドのひとつにいて,タクシーには乗っていない. そこから目的地のタクシースタンドまでの移動にかかる最短時間を求めなさい.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n p q
a1 b1 c1
…
ap bp cp
d1 e1 f1
…
dq eq fq
n, p, qはそれぞれタクシースタンドの数, 歩道の数,車道の数を表す. n は,2 以上の整数であり,20000 を超えない. タクシースタンドには 1 から n までの番号がついている. p, q は,どちらも正の整数であり,20000 を超えない. ai, bi, ci は i 番目の歩道を表す.それは ai 番と bi 番のタクシースタンドを結んでおり, 歩いて移動すると ci 分かかる. dj, ej, fj は j 番目の車道を表す.それは dj 番と ej 番のタクシースタンドを結んでいて, タクシーに乗って fj 分かかる. ai, bi, dj, ej はそれぞれ 1 以上 n 以下の整数である. ci, fj はそれぞれ 1 以上 106 以下の整数である.
入力の終わりは,3 つのゼロからなる行で表される. 全データセットについての n の合計,p の合計, q の合計はそれぞれ 200000 を超えない.
Output
各データセットについて, タクシースタンド 1 番からタクシースタンド n 番までの移動にかかる最短時間を分単位で表したものを 109+7 で割った余りを 1 行に出力せよ. 移動が不可能な場合は −1 を出力せよ.
Sample Input
5 4 2 1 2 1 2 3 100 3 4 1 4 5 100 2 3 10 4 5 10 4 1 1 1 2 100 2 3 100 4 3 3 1 2 10 2 3 1 3 4 10 2 1 2 3 2 2 4 3 2 0 0 0
Output for the Sample Input
25 -1 7
Problem F
完璧主義な王女様
王女様は n 人のスパイを従えており,ちょうど n 個の任務をスパイ達に割り当てようとしています. スパイの能力によって各任務が遂行可能かどうかが決まっています. 完璧主義な王女様としては,
- 各スパイがちょうど 1 つの任務を割り当てられ,
- 各任務がちょうど 1 人のスパイに割り当てられている
ようになっていないと満足できません.
幸いこれが可能であることは分かったのですが,自身が遂行可能な任務のうち特定のものに固執する我儘なスパイが出てくるかもしれません. 王女様は,我儘なスパイが 1 人いても満足できる任務割り当てが可能なようにスパイ達を訓練することにしました. 訓練 1 回で 1 人のスパイが新たな任務 1 つを遂行可能になります. 王女様は訓練回数をできる限り少なくしたいと思っています.
あなたに課せられた使命は,王女様に最適な訓練計画を提案することです. スパイと遂行可能な任務の組すべてが与えられます. 我儘なスパイがいなければ,王女様が満足できる任務割り当てが可能です. このとき,訓練を通して遂行可能な任務を増やすことで, 「どの 1 人のスパイが遂行可能などの任務に固執しても,王女様が満足できる任務割り当てが可能である」状態にする必要があります. なお,スパイは訓練の結果遂行可能になった任務に固執するかもしれません. また,まったく訓練を行わなくてもよいかもしれません.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n m
s1 t1
...
sm tm
- n はスパイの数を表す.任務の数も同じである. n は,正の整数であり,2000 を超えない.
- m はスパイと遂行可能な任務の組の数を表す. m は,正の整数であり,105 を超えない.
- スパイと任務は,それぞれ 1 から n までの整数で表す.
- 各 i = 1, 2, ..., m について (si, ti) は割り当て可能な組であり,スパイ si が任務 ti を遂行可能であることを表す. また,i ≠ j のとき,si ≠ sj または ti ≠ tj が成り立つ.
- 割り当て可能な組の部分集合であって,すべてのスパイと任務がちょうど 1 回ずつ現れるようなものが存在すること,すなわち,我儘なスパイがいなければ王女様が満足できる任務割り当てが可能であることが保証される.
入力の終わりは,2 つのゼロが空白区切りで並んだ行で表される. 入力に含まれるデータセットは 25 個以下である.
Output
各データセットについて,非負の整数 k を最初の行に出力し,続く k 行に xi と yi (i = 1, 2, ..., k) の 2 つの整数を空白区切りで出力せよ. k は訓練を行うスパイと任務の組の数の最小値,{(x1, y1), (x2, y2), ..., (xk, yk)} は最小値を達成する組の集合であり,xi と yi はそれぞれスパイと任務を表す. 訓練を行う組の集合であって要素数が最小のものは複数あるかもしれないが,そのいずれを出力しても正答と判定される.
Sample Input
2 3 1 1 1 2 2 2 2 2 1 1 2 2 4 7 1 1 1 2 2 2 3 2 3 3 3 4 4 4 5 10 1 1 1 2 1 3 2 1 2 2 2 4 3 3 4 4 4 5 5 5 0 0
Output for the Sample Input
1 2 1 0 2 2 3 4 1 2 3 2 5 3
Problem G
灯りの配置
いくつかの正方形のマスを並べた長方形のダンジョンの地図が与えられる. 各マスは壁か空きマスのいずれかである. ダンジョン内には開けた空間はない. 具体的には,以下の 2 つの条件を満たしている.
- ダンジョン内には全てが空きマスである 2 × 2 以上の大きさの領域はない.
- 斜め方向に空きマスが 3 つ連続することはない.
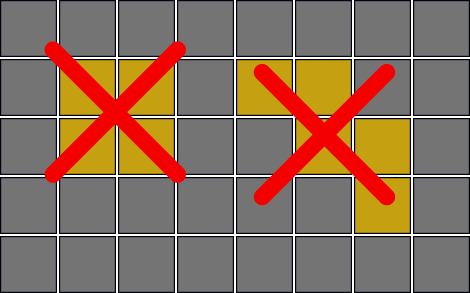
あなたは灯りをたくさん持っていて,灯りを空きマスに設置すれば,そのマスとそこから上下左右の 4 方向に一直線に連続する空きマスを全て明るくすることができる. 灯りは各空きマスに高々 1 つ設置でき,何個所に設置しても構わない.
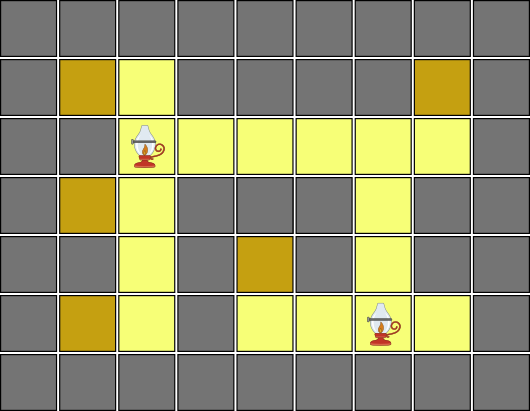
全ての空きマスを明るくするような灯りの配置の総数を求めよ.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n m
c1,1 ... c1,m
...
cn,1 ... cn,m
n, m はそれぞれ縦方向,横方向のマスの数を表し,1 ≤ n ≤ 30, 1 ≤ m ≤ 30 を満たす. ci,j は '#' または '.' の 1 文字で, '#' ならば上から i 番目,左から j 番目のマスは壁, '.' ならば空きマスである.
入力の終わりは,空白で区切られた 2 つのゼロだけからなる行で表される. データセットは 50 個以内である.
Output
各データセットについて,全ての空きマスを明るくするような灯りの配置の総数を 109+7 で割った余りを 1 行で出力せよ.
Sample Input
2 2 .# #. 3 3 ... .#. ... 2 3 #.. ..# 3 3 #.# ... #.# 3 5 .#.#. ..... #.#.# 0 0
Output for the Sample Input
1 161 9 25 243
Problem H
遁術
私はちょうど敵国の ICPC 城の内部で任務を済ませたところだ. この後はあらかじめ地下に掘っておいた脱出路から退散する算段だ. ただ,城内には n 棟の物見やぐらが等間隔に設置されており, 物見やぐらの見張りに気づかれないように脱出路の入口まで移動しなければならない.
ICPC 城の敷地は 100n × 100 の長方形の形状をしている. ここで,左奥角の座標を (0, 0),右手前角の座標を (100n, 100) としよう. 物見やぐらは 1 から n まで番号づけられており, k 番目の物見やぐらは座標 (100k − 50, 50) にある.
私の現在位置は座標 (x1, y1) であり, ここから敷地の中を移動しながら, 脱出路の入口がある (x2, y2) になるべく短い時間で到達したいと思っている.
物見やぐらの近くで高速に移動すると見張りが足音に気づいてしまう. 厳密には,最も近い物見やぐらまでの直線距離を D としたとき, 秒速 D2 以下で動かなければならない.
私は脱出路の入口まで最短何秒で移動できるだろうか.
例えば物見やぐらが 1 棟で,移動の開始地点(現在位置)と終了地点(脱出路の入口)の座標がそれぞれ (5, 6) と (78, 90) のとき,図 H-1 の経路をたどれば最も早く脱出できる. また,物見やぐらが 2 棟で,移動の開始地点と終了地点の座標がそれぞれ (85, 70) と (115, 30) のとき,図 H-2 の経路をたどれば最も早く脱出できる. これらは Sample Input の最初の 2 つのデータセットに対応している.
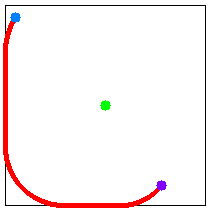 |
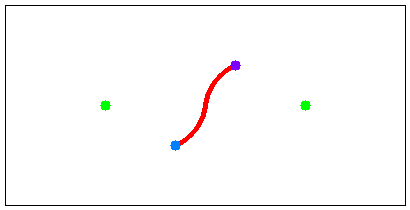 |
|
|
|
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n x1 y1 x2 y2
n は物見やぐらの数を表す. n は正の整数であり,107を超えない. (x1, y1) は移動の開始地点を表す. (x2, y2) は移動の終了地点を表す. x1 と x2 は,それぞれ整数であり,0 以上,100n 以下である. y1 と y2 は,それぞれ整数であり,0 以上,100 以下である. 移動の開始地点と終了地点の座標は異なる. また,移動の開始地点や終了地点の座標は,物見やぐらの座標とも一致しない.
入力の終わりは,5 つのゼロからなる行で表される. 入力に含まれるデータセットは 1000 個以下である.
Output
各データセットについて,移動にかかる最短時間(秒)を出力せよ. 出力は相対誤差または絶対誤差が 10−8 以下であれば許容される.
Sample Input
1 5 6 78 90 2 85 70 115 30 1 2 50 98 50 1 12 23 34 45 1 23 45 67 89 2 80 50 195 50 2 80 50 180 70 2 10 50 190 60 10 1 2 987 65 10 80 60 920 40 10 50 90 950 10 0 0 0 0 0
Output for the Sample Input
0.056924948365 0.024806946918 0.060137708723 0.039815727511 0.054616382922 0.070423053859 0.063218824369 0.091771006495 0.338081602957 0.297714980979 0.316557291903
