Links
Problem A
Counting Peaks of Infection
For the new infectious disease, COVID-99, numbers of new positive cases of PCR tests conducted in the city are reported daily. You are requested by the municipal public relations department to write a program that counts the number of the peaks so far of the positive cases.
Here, the number of peaks is the number of days on which the number of positive cases reported is more than both of the day before and the next day.
As the PCR tests started before the disease started spreading in the city, the number of positive cases is zero on the first day. The last reported day is not counted as a peak. No two consecutive days have the same number of positive cases.
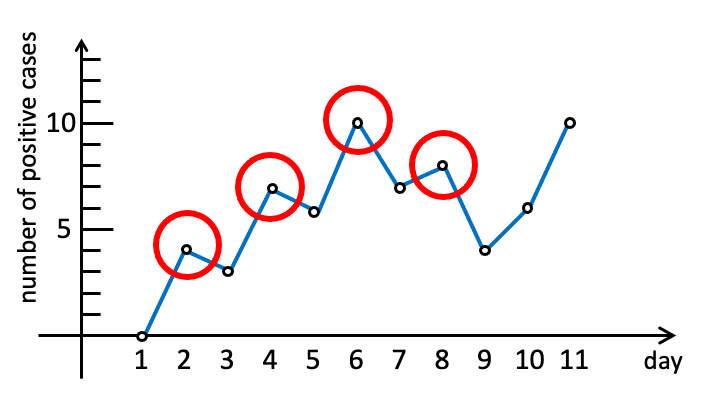
Figure A-1: Numbers of positive cases of the last dataset in Sample Input. Red circles indicate the peaks.
Input
The input consists of multiple datasets. Each dataset is in the following format.
n
v1 ... vn
n is the number of days on which the numbers of positive cases are reported (3 ≤ n ≤ 1000). vi is the number of positive cases on the i-th day, an integer between zero and 1000, inclusive. Note that v1 is zero, and vi ≠ vi+1 for 1 ≤ i < n, as stated above.
The end of the input is indicated by a line containing a zero. The input consists of at most 100 datasets.
Output
For each dataset, output the number of peaks in a line.
Sample Input
3 0 1000 0 5 0 1 2 0 1 3 0 1 2 7 0 1 0 1 8 7 6 11 0 4 3 7 6 10 7 8 4 6 10 0
Output for the Sample Input
1 1 0 2 4
Problem B
Leave No One Behind
A card game similar to Old Maid is played by n players P1, ..., and Pn, sitting clockwise in this order.
For this game, n pairs of cards numbered 1 through n are used. Each player has two cards at hand to start with.
First, any player who has a pair of cards with the same number discards them. If by chance all the players discard the cards in hand, the game ends. Otherwise, the following actions are repeated until the game ends. Note that, from now on, for a player p, the next player means the player closest to p in the clockwise direction among those who still have one or more cards at that point in time.
- Choose the player p as follows.
- For the first turn, choose P1. If, however, P1 has no cards, choose the next player of P1.
- For the second and subsequent turns, choose the next player of the one chosen for the previous turn.
- The next player of p, say p′, looks at the card(s) in the hand of p and draws the one having the smallest number among them.
- If that makes a pair of cards with the same number in the hand of p′, the pair is discarded. If no cards remain in any players' hands at this point, the game ends.
Figure B-1 shows the initial hands of the three players of the second dataset in Sample Input. Immediately after, the player P1 discards the two cards in the hand. p of the first turn is P2 because P1 has no cards.

Figure B-1: The initial hands of the second dataset in Sample Input
Figure B-2 shows the hands of the five players of the last dataset in Sample Input after the following actions:
- P1 is chosen first and the next player of P1, that is, P2, draws the card with the smallest number 1 from the P1's hand. P2 has three cards with numbers 1, 3, and 5 in hand at the end of this turn;
- P3, P4, and P5, in this order, draw the same card with the number 1 that was initially in the P1's hand; and
- P5 discards the pair of cards with the number 1.
After this, P1 draws the only remaining card in P5's hand and discards the drawn card and the card with the same number 2 in the hand. The player to be drawn from the hand next is the next player of P5, which is P2 because P1's hand is empty now.

Figure B-2: The hands of the last dataset in Sample Input after the fourth turn
Since at least one pair of cards is discarded between two drawings from the hand of the same player, the game will end sooner or later. Unlike Old Maid, no cards will be left in the hand of any player at the end.
Write a program that, for given initial hands of all the players, computes the number of times cards are drawn by the end of the game.
Input
The input consists of multiple datasets, each in the following format.
n
c1,1 c1,2
⋮
cn,1 cn,2
n is the number of players. n is an integer no less than two and no more than 1000. ci,1 and ci,2 are the numbers on the two cards in the initial hand of Pi (1 ≤ i ≤ n). Each integer between 1 and n, inclusive, appears exactly twice in c1,1, c1,2, ..., cn,1, and cn,2.
The end of the input is indicated by a line containing a zero. The input has at most 10000 lines.
Output
For each dataset, output a single line containing the integer that is the number of times cards are drawn.
Sample Input
3 1 1 2 2 3 3 3 1 1 2 3 3 2 3 1 3 2 1 3 2 5 1 5 5 4 4 3 3 2 2 1 5 1 2 3 5 4 3 1 4 5 2 5 1 2 3 5 4 3 5 4 1 2 0
Output for the Sample Input
0 2 3 14 8 8
Problem C
Training Schedule for ICPC
With little time remaining until ICPC, you decided to reschedule your training plan. As maintaining both mental and physical vitality is important, you decided to spend n days of the remaining n + m days for training, and m days for repose. The question is which days should be used for the training and which for the repose. A schedule that increases your ICPC power more is better.
Training days increase the power, and consecutive training days are more effective. One day of training on the k-th day of consecutive training days increases the power by 2k − 1, where k = 1 for the first day of the consecutive training days. A single training day increases the power by only 1, but two consecutive training days increase it by 1 + 3 = 4, and three consecutive training days increase it by 1 + 3 + 5 = 9.
Repose days, on the other hand, decrease the power, and consecutive repose days decrease it more rapidly. One day of repose on the k-th day of consecutive repose days decreases the power by 2k − 1, where k = 1 for the first day of the consecutive repose days. A single repose day decreases the power by only 1, but two consecutive repose days decrease it by 1 + 3 = 4, and three consecutive repose days decrease it by 1 + 3 + 5 = 9.
Let us compute the largest increment of your ICPC power after n + m days of training and repose by the best training schedule. Note that, if you have too many repose days, this may be negative.
Input
The input consists of multiple datasets, each in the following format.
n m
Here, n and m are the numbers of training and repose days, respectively. Neither of them exceeds 106, and at least one of them is non-zero.
The end of the input is indicated by a line containing two zeros. The number of datasets does not exceed 100.
Output
For each of the datasets, output in a line the largest increment of ICPC power after n + m days of training and repose by the best training schedule.
Sample Input
1 1 3 2 6 1 1 6 0 3 2 4 7 9 0 0
Output for the Sample Input
0 7 35 -17 -9 -4 10
Problem D
Audience Queue
You are working as a staff member at a concert venue, organizing the audience queue. Everyone in the queue holds one ticket with a seat number printed. The seat numbers are integers from 1 to n without duplicates. Since this is a very popular concert, all the seats are reserved and exactly n people are in a single line.

Figure D-1: An example of the audience queue (The first dataset in Sample Input)
Your job is to split the line at some points and navigate each of the sublines to a distinct entrance gate. The audience are so polite that the order in each of the sublines is kept. There are k entrance gates, and thus you can split the line into k or less sublines. Sublines may have widely varying lengths, but empty sublines are not allowed. In the example of the figure below, the original line [4 2 3 5 1] has been split into three sublines, [4 2], [3 5], and [1].
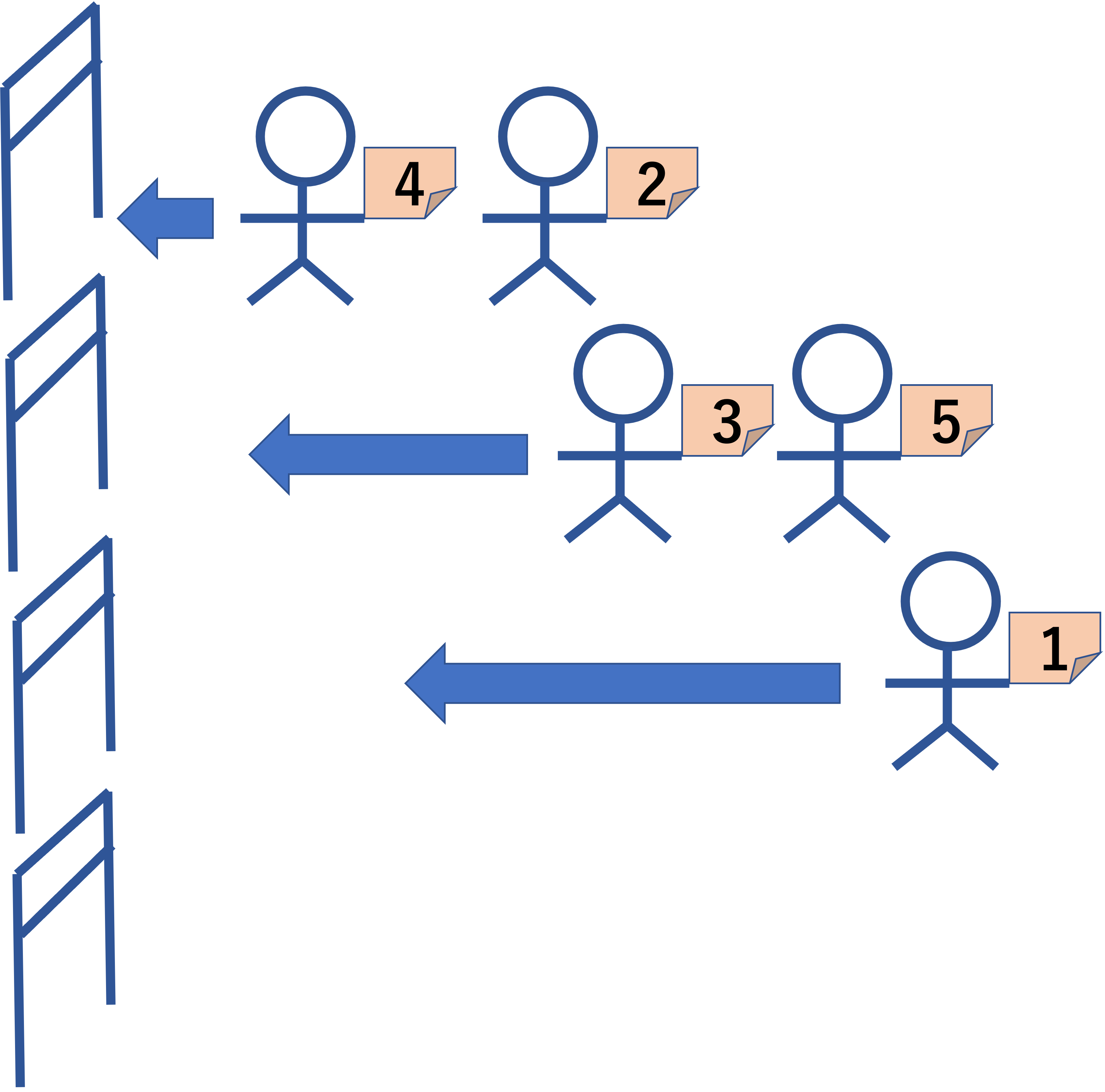
Figure D-2: An example of splitting the line
Although up to k lines are formed, the audience can enter the hall one at a time. Among those who head the lines, one with the smallest seat number enters the hall first. In the example figure below, among the heads 4, 3, and 1 of the lines, one with the smallest seat number, 1, enters the hall first. Subsequent entrance order is decided in the same way. Among those who head the lines at the time, one with the smallest seat number is the next to enter the hall.

Figure D-3: An example of the order of the entrance
The order of entrance depends on how you split the audience line. Different ways of splitting may result in the same order. For the example above, splitting into [4 2], [3], [5], and [1] results in the same order.
Given the initial order in the queue and the final entrance order of the audience, please compute how many different ways of splitting the line result in the given final entrance order. For the same partitioning of the line, different assignments of sublines to gates are not counted separately.
Input
The input consists of multiple datasets, each in the following format.
n k
s1 ... sn
t1 ... tn
Integers n and k satisfies 1 ≤ k ≤ n ≤ 104. The number of the people in the audience line is represented by n, and the number of the gates is represented by k. The sequence s1 ... sn is a permutation of the integers 1 through n, which describes the initial order of the audience in the queue. The sequence t1 ... tn is also a permutation of the integers 1 through n, which describes the final entrance order.
The end of the input is indicated by a line "
Output
For each dataset, output in a line the number of ways to split the line as described in the problem statement.
Since the number can be very large, the output should be the number modulo the prime number
Sample Input
5 4 4 2 3 5 1 1 3 4 2 5 3 3 1 2 3 1 2 3 3 2 3 2 1 1 2 3 7 5 4 5 6 7 1 2 3 1 2 3 4 5 6 7 4 4 2 1 4 3 1 4 3 2 31 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 0
Output for the Sample Input
2 4 0 26 0 75497471
Problem E
Village of Lore
Icpca village, said to lie in a deep jungle, is known by strange, contradictory lore. Some say there lies a epitome of happiness while others say it is a terrible fortress of horror.
An old soothsayer, who is a precious source of information, reported that Icpca village has a rectangular form with streets of a grid pattern. n west-east straight streets and m north-south straight streets pass through the village. n and m are both even. To investigate the reality of the lore, a team of n + m researchers were sent to Icpca village. The plan of the investigation was as follows.
- The i-th of the first n researchers walks from the western end to the eastern end on the i-th street from the north.
- The j-th of the remaining m researchers walks from the northern end to the southern end on the j-th street from the west.
Some of the researchers returned from Icpca village as planned. However, nothing has been heard from the rest...
According to the pseudopsia of the old soothsayer, there stands exactly one statue on each of the nm intersections of west-east and north-south streets in Icpca village. Each statue is either beautiful or horrible.
Each researcher has a value called sanity. All the researchers have the sanity of 0 before they start the investigation. When a researcher comes to an intersection with a beautiful statue, his/her sanity is increased by 1. When a researcher comes to an intersection with a horrible statue, his/her sanity is decreased by 1. Since the horrible statues are extraordinarily horrible, if the sanity of a researcher becomes negative, he/she cannot move anymore because of the fear, and will never return from the village. Since the beautiful statues are extraordinarily beautiful, if the sanity of a researcher is positive on going out of the village, the euphoria prevents him/her from leaving the village. The rest of the researchers, those who keep non-negative sanity and have the sanity of 0 on exiting the village, will return.
The investigation is over, regrettably with many missing persons. Now you have the list of returned researchers. Your task is to decide whether there exist any arrangements of beautiful and horrible statues not conflicting with the list, and, if any, show one of such arrangements.
Input
The input consists of multiple datasets, each in the following format.
n m
A
B
n and m are the numbers of west-east and north-south streets, respectively.
n and m are both positive even numbers at most 100.
A and B are strings representing whether each researcher has returned from the village.
A has the length n and B has the length m.
Each string consists only of
The number of datasets does not exceed 100. The end of the input is indicated by a line containing two zeros.
Output
For each dataset, if there exists no statue arrangement that does not contradict the list, output
Note that there may be multiple arrangements not contradicting the list. Any such output is judged as a correct output.
Sample Input
2 2 10 10 2 2 11 11 4 6 0010 100011 0 0
Output for the Sample Input
Yes +- -+ No Yes +---++ ----++ +++--- ---+--
Problem F
Trim It Step by Step
The intelligence agency of the Kingdom uses a unique encryption method; a nonempty message consisting only of lowercase letters is encrypted into an expression <expr> complying with the grammar described by the following BNF.
<expr> ::= <char> | <expr><expr> | ?(<expr>)<char> ::= a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z
The original message before encryption is the string appearing first in the lexicographic order among the possible results of applying the procedure described below to the encrypted message.
Procedure: Repeat the following operation while ? remains in the expression.
- Choose any occurrence of a contiguous substring of the form
?(s)(possibly the whole expression) such that s does not contain any symbols?,(, or). - If s is empty, simply remove the chosen occurrence of
?(). - Otherwise, replace the chosen occurrence of
?(s)with the string obtained from s by deleting either the first or the last character.
For example, consider the expression ?(?(icp)c).
Then, ?(icp) is the only occurrence that can be chosen, and this part is replaced with either cp or ic.
Thus, the whole expression becomes either ?(cpc) or ?(icc).
After that, by choosing the whole expressions and replace them, there are four possible results, pc, cp, cc, and ic.
The original message is cc, which appears first in the lexicographic order among them.
You, an intelligence agent of the Republic, hostile to the Kingdom, have succeeded in obtaining an encrypted message, that is, an expression described above. Find the original message.
Input
The input consists of multiple datasets. The first line of the input consists only of the number n of the datasets, where n does not exceed 50. The following n lines give the datasets, one in each line.
Each dataset is given in a single line consisting only of an expression <expr> complying with the grammar described by the BNF in the problem statement, and the expression consists of at most 1000 characters including symbols.
Output
For each dataset, output in a line the string appearing first in the lexicographic order among the possible results of applying to it the procedure in the problem statement. It is guaranteed that the correct output is never an empty string.
Sample Input
6 ?(icpc) ?(?(icpc)) ?(ic)?(pc) ?(?(icp)c) ?(i?(?(c))pc) ?(bca)?(?(bca))
Output for the Sample Input
cpc cp cc cc ip bca
Problem G
Keep in Touch
Two agents A and B, known as a great combination, are conducting the infiltration mission to a secret base. Due to the strict security of the base, two agents have decided to follow the prechecked safe infiltration routes RA and RB, respectively. Each infiltration route is a two-dimensional polyline, a series of line segments.
Each of the agents starts at the starting end of the first segment of the corresponding route. The mission is over when both agents are on the finishing ends of the last segments of their routes simultaneously.
During the mission, each of the agents can move forward or backward at an arbitrary speed, or stop for a moment, as long as the movements along the route are continuous, but cannot jump changing the position abruptly. Although segments of a route may have crosses or overlaps with one another, they cannot be used for movements. Precisely, an agent on one segment can transfer to another segment only in the following cases.
- The destination segment is the next segment on the route, and the agent is on the finishing end of the current segment.
- The destination segment is the previous segment on the route, and the agent is on the starting end of the current segment.
For example, in Figure G-1 below, the agent must move to the finishing end of the segment 3-4 of RB, (−1, 1), in order to transfer to the segment 4-5. Although, the agent passes the same point as the finishing end of the last segment, (2, 1), when the agent transfers from the segment 2-3 to the segment 3-4, the agent is not considered to be on the finishing end of the last segment at that time.
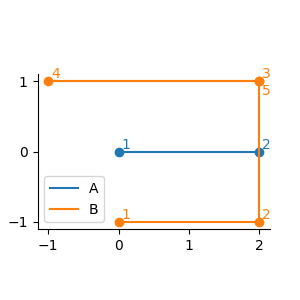
Figure G-1: Infiltration routes for the first dataset of Sample Input
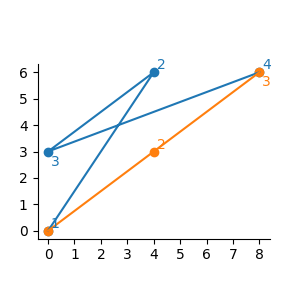
Figure G-2: Infiltration routes for the second dataset of Sample Input
To prepare for the contingency, the agents carry radio communicators and they should always be within the range allowing communication between them. Stronger wave enables longer communication distance, but increases the interception possibilities. Give the minimum required communication distance to accomplish the mission with appropriate movements of the agents.
Input
The input consists of multiple datasets, each in the following format.
n
xA,1 yA,1
⋮
xA,n yA,n
m
xB,1 yB,1
⋮
xB,m yB,m
n is the number of the vertices of the infiltration route RA. n is an integer between 2 and 40, inclusive.
xA,i and yA,i (1 ≤ i ≤ n) are the coordinates of the i-th vertex. xA,i and yA,i are integers satisfying −1000 ≤ xA,i ≤ 1000 and −1000 ≤ yA,i ≤ 1000, respectively. For 1 ≤ i ≤ n−1, (xA,i, yA,i) is the starting end of the i-th line segment, and (xA,i+1, yA,i+1) is its finishing end. All line segments have non-zero lengths. That is, xA,i ≠ xA,i+1 and/or yA,i ≠ yA,i+1 holds.
m and the value pairs of xB,j and yB,j (1 ≤ j ≤ m) represent the infiltration route RB. The format and the constraints are the same as those for RA.
The end of the input is indicated by a line containing a zero. The number of datasets does not exceed 50.
Output
For each dataset, output in a line the maximum distance between the two agents during the mission when they move in a way that minimizes the maximum distance. The error contained in the output should not exceed 10−8. The output shall be deemed correct if its relative error or its absolute error is within this limit.
Sample Input
2 0 0 2 0 5 0 -1 2 -1 2 1 -1 1 2 1 4 0 0 4 6 0 3 8 6 3 0 0 4 3 8 6 10 40 15 40 20 40 15 45 10 50 12 50 10 50 15 60 15 65 20 70 18 10 40 10 40 15 45 20 50 18 50 15 50 20 60 20 60 15 65 10 70 12 0
Output for the Sample Input
1.414213562373 2.400000000000 9.284766908853
Problem H
Artist in Agony
You, an artist, prepared a sufficient number of balls and also strings to link them for your artwork. Balls are to be given sequential numbers eventually, but only one of the balls is given number 1 at the beginning. No other balls are numbered and no balls are linked to any other balls yet.
An artwork is created by carrying out either of the following actions repetitively.
- Replication:
- The work in progress is replicated. Let n be the number of balls numbered so far. You pick n unnumbered balls and number them n+1, ..., 2n. This results in 2n balls uniquely numbered 1 through 2n. Then for all pairs of balls linked directly before replication numbered u and v, the two balls newly numbered n+u and n+v are linked with a string.
- Making a new link:
- Two distinct balls already numbered are chosen and linked with a string. When two balls are already linked directly, this action does nothing.
Note that, as initially only one ball is numbered, you have to start with the replication action.
Figure H-1 shows the process of artwork creation of the second dataset in Sample Input.
Figure H-1: Artwork creation example
Being a perfectionist as with all the real artists, you cannot stand imperfect works. When you find a work unsatisfactory, you have to destroy it completely as quick as possible by tearing off all the links in it. You grab some of the numbered balls in one hand, the rest in the other hand, and pull them apart tearing off all the strings linking the balls in your right hand and the balls in your left hand. If all the strings linking the balls are torn off by doing this operation just once, your destruction is successful. Conversely, any remaining links between two balls in one hand mean that the destruction is a failure.
Figure H-2 shows the work of the second dataset in Sample Input being destroyed. To destroy the work, you have to grab three or more balls in each of your hands.
Figure H-2: Destructing the artwork described above
Given the sequence of actions that created the work, judge whether you can destroy it in the way described above. If you can, find the minimum number of balls you have to grab in your left hand. You may grab an arbitrary number of balls in your right hand.
Input
The input consists of multiple datasets, each in the following format.
m
a1
⋮
am
m is the number of actions you have carried out. m is a positive integer and does not exceed 300.
The i-th action ai (i = 1, ..., m) is given by either of the following forms.
COPY-
This represents the Replication action in the problem statement. It is guaranteed that each dataset contains no more than 60
COPYactions. LINKu v- This represents the Making a new link action in the problem statement. In this action, the two balls numbered u and v were inspected, and a new link between them was made if they had not been directly connected yet. u and v are positive integers that satisfy u < v. It is guaranteed that two balls had already been numbered u and v at that time.
The end of the input is indicated by a line containing a zero. The number of datasets does not exceed 100.
Output
For each of the datasets, output one line containing an integer. If you can destroy the work in the way described above, output the minimum number of balls you need to grab in your left hand. Otherwise, output −1.
Sample Input
3 COPY LINK 1 2 COPY 8 COPY COPY LINK 1 2 LINK 1 3 LINK 1 3 COPY LINK 5 6 LINK 3 6 5 COPY LINK 1 2 COPY LINK 1 3 LINK 2 3 2 COPY COPY 0
Output for the Sample Input
2 3 -1 0
