Links
Problem A
感染ピークの回数
新しい感染症 COVID-99 について,市内の PCR 検査で判明した日ごとの新規陽性者数が報告されている. あなたは市の広報部門からこれまでの新規陽性者数のピークの回数を数えるプログラムの作成を依頼されている.
ここでピークの回数とは,前日と翌日のどちらよりも報告された新規陽性者数が多かった日の数である.
市内でこの感染症が広がり始める前に PCR 検査を始めたので,最初の日の新規陽性者数はゼロである. 報告の最終日はピークに数えない. なお,同数の日が連続することはない.
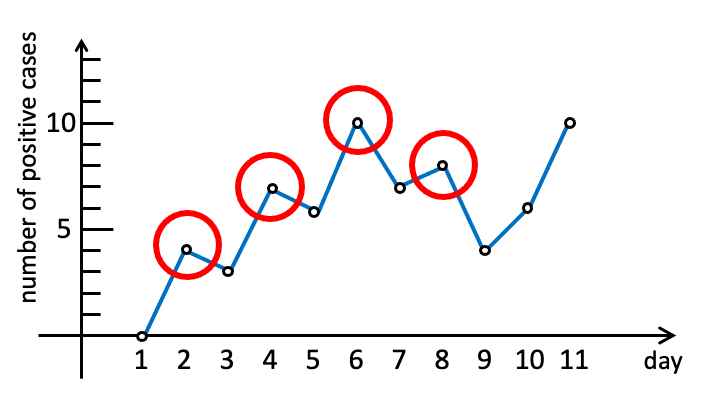
図 A-1: Sample Input の最後のデータセットの新規陽性者数.ピークを赤丸で示している.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n
v1 ... vn
n は新規陽性者数の報告があった日数である (3 ≤ n ≤ 1000). vi は i 日目の新規陽性者数で,0 以上 1000 以下の整数である. なお上述のように,v1 は 0 であり, 1 ≤ i < n である i に対して vi ≠ vi+1 である.
入力の終わりは,ひとつのゼロからなる行で表される. 入力に含まれるデータセットは 100 個以内である.
Output
各データセットに対して,ピークの回数を 1 行に出力せよ.
Sample Input
3 0 1000 0 5 0 1 2 0 1 3 0 1 2 7 0 1 0 1 8 7 6 11 0 4 3 7 6 10 7 8 4 6 10 0
Output for the Sample Input
1 1 0 2 4
Problem B
誰ひとり取り残さない
n 人のプレイヤー P1, ..., Pn がこの順番で時計回りに座って,ババ抜きに似たカードゲームを行う.
このゲームでは,1 から n までの各番号が書かれたカードを 2 枚ずつ使う.最初に各プレイヤーはカードを 2 枚持っている.
まず,同じ番号のカードを 2 枚持っているプレイヤーは,それらのカードを場に捨てる.もし万一全員がカードを捨ててしまったら,ここでゲームは終了する.そうでなければ,ゲームが終了するまで,以下の動作を繰り返し行う.これ以降,プレイヤー p に対して,「次のプレイヤー」は,その時点でまだ手札が 1 枚以上残っているプレイヤーのうち,時計回りの方向で p から一番近い者を意味する.
- 次のようにプレイヤー p を選ぶ,
- 1 回目は P1 を選ぶ.ただし,P1 の手札が残っていなければ,P1 の次のプレイヤーを選ぶ.
- それ以降は,前の回で選ばれたプレイヤーの次のプレイヤーを選ぶ.
- p の次のプレイヤー p′ は,p の手札を見て,その中で最小の番号のカードを引く.
- p′ が同じ番号のカードを 2 枚持つようになった場合には,その 2 枚のカードを場に捨てる.この結果,すべてのプレイヤーのカードがなくなったら,ゲームは終了する.
図 B-1 は,Sample Input で 2 番目のデータセットにおける 3 人のプレイヤーの初期手札を示している.この直後に,P1 は手札の 2 枚のカードを捨てる.1 回目の p は P2 である.なぜならば,P1 の手札は空になっているからだ.

図 B-1: Sample Input の 2 番目のデータセットの初期手札
図 B-2 は,Sample Input の最後のデータセットで,以下の動作が終わった後の 5 人のプレイヤーの手札を示している.
- P1 がまず選ばれ,P1 の次のプレイヤー(すなわち P2)が P1 の手札の中から最小の番号 1 のカードを引く.この回の終わりに,P2 は 1, 3, 5 の番号の 3 枚のカードを持つ.
- P3, P4, P5 がこの順番に同じカード(最初は P1 の手札にあった番号 1 のカード)を引く.
- P5 が,同じ番号 1 のカード 2 枚を捨てる.
この後,P1 が P5 の手札から唯一残ったカードを引き,このカードと自分の手札の中の同じ番号 2 のカードを捨てる.次に手札を引かれるのは,P5 の次のプレイヤーであり,P1 の手札は空になっているので,それは P2 である.

図 B-2: Sample Input の最後のデータセットで,4 回目の動作の後の手札
同じプレイヤーが 2 回手札を引かれる間に,少なくとも 1 対のカードが捨てられるので,遅かれ早かれゲームは終わる. ババ抜きとは異なり,最後にカードは残らない.
全プレイヤーの最初の手札が与えられた時,ゲームが終了するまでに何回カードが引かれるかを求めるプログラムを作成せよ.
Input
入力は複数のデータセットからなり,各データセットは次の形式で表される.
n
c1,1 c1,2
⋮
cn,1 cn,2
n はプレイヤーの人数を表す. n は,2 以上 1000 以下の整数である. ci,1 と ci,2 は Pi の最初の手札の 2 枚のカードの番号である (1 ≤ i ≤ n).1 から n までの各整数が,c1,1, c1,2, ..., cn,1, cn,2 の中にちょうど 2 回ずつ現れる.
入力の終わりは,ゼロだけからなる行で表される.入力のサイズは 10000 行以下である.
Output
各データセットについて,カードが引かれる回数を表す 1 つの整数からなる行を出力せよ.
Sample Input
3 1 1 2 2 3 3 3 1 1 2 3 3 2 3 1 3 2 1 3 2 5 1 5 5 4 4 3 3 2 2 1 5 1 2 3 5 4 3 1 4 5 2 5 1 2 3 5 4 3 5 4 1 2 0
Output for the Sample Input
0 2 3 14 8 8
Problem C
ICPC に向けての練習日程
ICPC までに残された時間は少なくなり,あなたたちは練習計画を練り直すことにした.気力体力の温存も大切なので,残る n + m 日のうち n 日を練習に,m 日は休息に充てることにする.問題はどの日を練習日,どの日を休息日とするのがよいかだ.練習計画は ICPC 能力 をより高めるものほどよい.
練習日は能力を高め,練習日が連続すると効果はさらに大きくなる.連続する練習日の k 日目の練習では能力が前日より 2k − 1 だけ高まる (連続する練習日の初日を k = 1 とする).1 日だけの練習では能力は 1 しか高まらないが,2 日続ければ 1 + 3 = 4 高まり,3 日続ければ 1 + 3 + 5 = 9 も高まることになる.
一方,休息日は能力を落とし,続けて休息日をとると能力がどんどん低下していく.連続する休息日の k 日目には能力が前日より 2k − 1 だけ低下する (連続する休息日の初日を k = 1 とする).1 日だけの休息なら能力が 1 低下するだけだが,2 日続けると 1 + 3 = 4,3 日続ければ 1 + 3 + 5 = 9 も低下してしまう.
最善の練習計画によって n + m 日間の練習と休息の後に達成できる ICPC 能力の最大増分を求めよ.休息日が多いとこの値は負になってしまうこともあることに注意.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n m
ここで n と m はそれぞれ練習日と休息日の日数である. どちらも 106 を超えることはなく,少なくとも一方はゼロでない.
入力の終わりはゼロふたつからなる行で表される. データセットは 100 個以内である.
Output
各データセットについて,最善の練習計画によって n + m 日間の練習と休息の後に達成できる ICPC 能力の最大増分を 1 行に出力せよ.
Sample Input
1 1 3 2 6 1 1 6 0 3 2 4 7 9 0 0
Output for the Sample Input
0 7 35 -17 -9 -4 10
Problem D
入場待ちの行列
あなたはコンサート会場のスタッフとして聴衆の行列の整理にあたっている. 入場希望者は各自,座席番号の記されたチケットを一枚ずつ所持している. 座席番号は 1 から n までの整数で,重複はない. 人気のコンサートなので,座席は既に予約で満席になっており,ちょうど n 人が一列に並んでいる.

図 D-1: 入場列の例 (Sample Input の最初のデータセット)
あなたに任されている仕事は,この入場列を適当な何カ所かで区切って,それぞれの列を別々の入場ゲートに案内することである. 聴衆は皆礼儀正しいので区切られた列の中の順序が変わることはない. 入場ゲートは k カ所あるので,元の列を k 本以内の列に分割できる. 各列の長さは大きく異なっても良いが,空の列を作ってはならない. 下図の例では,元の列 [4 2 3 5 1] を 3 本の列 [4 2], [3 5], [1] に分割している.
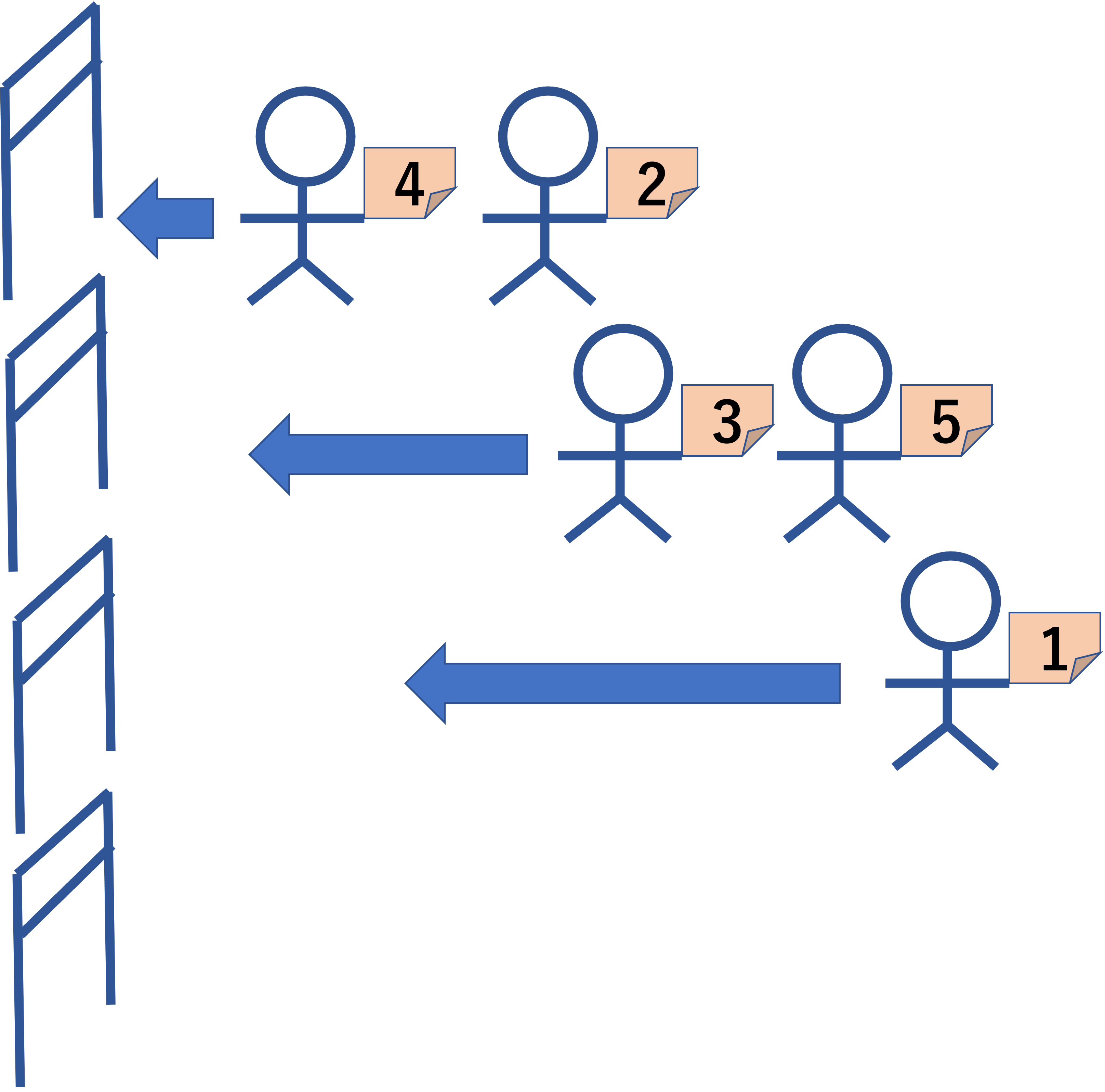
図 D-2: 列の分割の例
最大 k 本の列はできるが,聴衆は一人ずつしか会場に入っていけない. この際,各列の先頭のなかで,最も小さい座席番号の人が最初に入場する. 以下の図の例では先頭の 4, 3, 1 のうち最小の座席番号 1 番のチケットを持った人が最初に入場できる. その後の入場順も同様で,各列の先頭のなかで最も小さい座席番号の人が次の入場者となる.
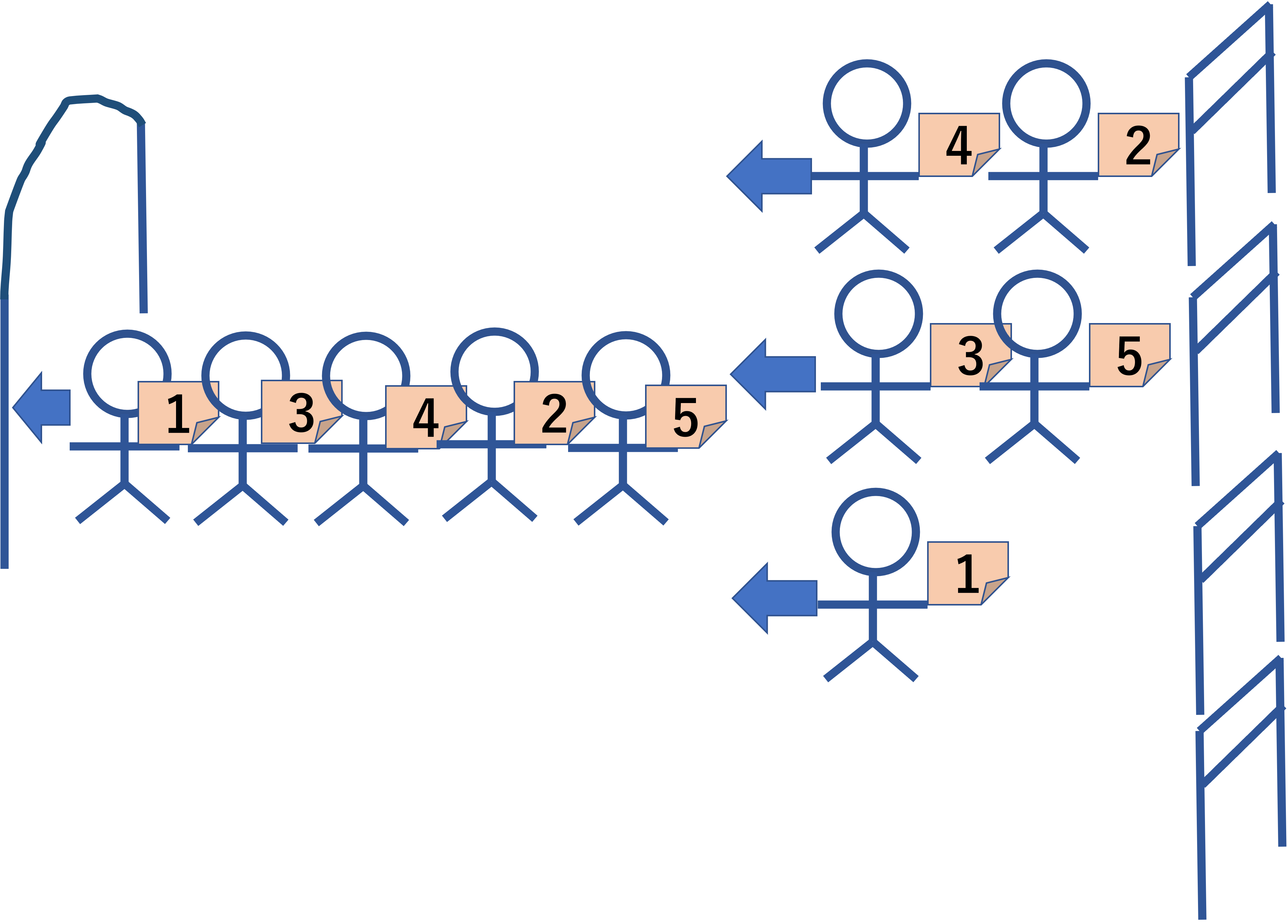
図 D-3: 入場の順の例
聴衆の列をどこで分割するかを決めると入場順が決まる. 異なる分割で同じ入場順になるかもしれない. 上の例では,[4 2], [3], [5], [1] と分割しても同じ入場順になる.
聴衆の最初の並び順と,実現したい最終的な入場順が与えられたとき,その入場順になるような列の分割の仕方が何通りあるか,計算してほしい. 分割の仕方が同じなら,どの列をどのゲートに案内するかは区別しない.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n k
s1 ... sn
t1 ... tn
整数 n, k は 1 ≤ k ≤ n ≤ 104 を満たし, n が列に並ぶ聴衆の人数を,k がゲートの数を表す. s1 ... sn は 1 から n までの整数を並べかえた列であり,聴衆の最初の並び順を表す. t1 ... tn も同様に 1 から n までの整数を並べかえた列であり,実現したい最終的な入場順を表す.
入力の終わりは,"
Output
各データセットについて,題意を満たす分割の仕方が何通りあるかを 1 行に出力せよ.
答えはとても大きくなり得るため,出力するのは素数
Sample Input
5 4 4 2 3 5 1 1 3 4 2 5 3 3 1 2 3 1 2 3 3 2 3 2 1 1 2 3 7 5 4 5 6 7 1 2 3 1 2 3 4 5 6 7 4 4 2 1 4 3 1 4 3 2 31 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 0
Output for the Sample Input
2 4 0 26 0 75497471
Problem E
伝承の村
密林の奥深くに位置するという Icpca 村は,相反する奇妙な伝承で有名である. 一説には,そこは具現化された幸福であるという.一説には,そこは身の毛もよだつ恐怖の要塞であるという.
数少ない情報源である老占者によれば,Icpca 村は長方形で,道路は格子状に整備されており,東西方向に n 本,南北方向に m 本の道路がそれぞれまっすぐに村を貫いているらしい. なお,n と m はともに偶数である. 伝承の真相を探るため,n + m 人からなる調査チームが Icpca 村に派遣された.調査計画は以下の通りであった.
- 最初の n 人の調査員のうち i 人目は,東西方向の道路のうちの北から i 本目を,西端から東端に向かって歩く.
- 残る m 人の調査員のうち j 人目は,南北方向の道路のうちの西から j 本目を,北端から南端に向かって歩く.
調査員のうち何人かは,予定通りに Icpca 村から帰還した.しかしながら残りの調査員は,いまだに音信不通のままだ……
老占者の幻視によれば,Icpca 村の東西方向と南北方向の道路の交わる nm 個の交差点には,それぞれ石像がちょうど 1 体立っているという. 石像には美しい像と恐ろしい像の二種類があり,すべての像はそのどちらかである.
各調査員は正気度と呼ばれる値を持っており,Icpca 村に入る時点では,すべての調査員の正気度は 0 であった. 調査員の正気度は,美しい像のある交差点にさしかかると 1 増加する.また,恐ろしい像のある交差点にさしかかると 1 減少する. 恐ろしい像はとても恐ろしいので,途中で正気度が負になった場合,調査員はその場で動けなくなって,村に取り残されてしまう. 美しい像はとても美しいので,もし Icpca 村を出る時点で正気度が正なら,調査員は村から出るのを嫌がり,やはり村に取り残されてしまう. どちらにも当てはまらない調査員,すなわち,途中で正気度が負にならず,村を出る時点で正気度が 0 であった調査員だけが,無事に村から帰還できる.
多くの遭難者を出しながらも調査は完了した.あなたは帰還した調査員のリストを持っている. あなたの仕事はリストと矛盾しない美しい像と恐ろしい像の配置がありうるかを判定し,あるならそのひとつを求めることである.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n m
A
B
n, m はそれぞれ,東西方向と南北方向の道路の本数を表す.
n, m は,正の偶数であり,100 を超えない.
A, B は それぞれ,各調査員が村を通過できたかを表す文字列である.
A は長さ n の,B は長さ m の,それぞれ
データセットの個数は 100 を超えない. 入力の終わりは,ゼロふたつからなる行で表される.
Output
各データセットについて,リストと矛盾しない像の配置が存在しなければ 1 行に
リストと矛盾しない像の配置は複数あるかもしれないが,そのいずれを出力しても正答と判定される.
Sample Input
2 2 10 10 2 2 11 11 4 6 0010 100011 0 0
Output for the Sample Input
Yes +- -+ No Yes +---++ ----++ +++--- ---+--
Problem F
じわじわ削れ
王国の諜報機関は独特の暗号化方式を使っており,英小文字のみからなる空でない文字列である通信文を,以下の BNF で記述される文法に従う式 <expr> に暗号化する.
<expr> ::= <char> | <expr><expr> | ?(<expr>)<char> ::= a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z
暗号化前の通信文は,以下に述べる手順を暗号文に適用した結果としてあり得る文字列のうち,辞書式順序で最初に現れるものである.
手順: 式中に ? が残っている限り,以下の操作を繰り返す.
?(s)という形の連続部分文字列であって,s に記号?,(,)を含まないようなものの出現(式全体でもよい)を任意に 1 つ選ぶ.- s が空文字列であれば,選んだ
?()の出現を単に取り除く. - そうでなければ,選んだ
?(s)の出現を,s の先頭または末尾 1 文字を取り除いた文字列で置き換える.
たとえば ?(?(icp)c) という式を考えてみよう.このとき,選べる出現は ?(icp) のみであり,この部分が cp または ic に置き換えられる.したがって,式全体は ?(cpc) または ?(icc) となる.さらに,それぞれの式全体を選んで置き換えると,結果としてあり得る文字列は pc, cp, cc, ic の 4 種類である.このうち,辞書式順序で最初に現れる cc が暗号化前の通信文である.
敵対する共和国の諜報員であるあなたは,暗号文,すなわち上述の式を入手することに成功した.暗号化前の通信文を求めよ.
Input
入力は複数のデータセットからなる.入力の 1 行目はデータセットの個数 n のみからなり,n は 50 を超えない.続く n 行に,1 行に 1 つずつデータセットが与えられる.
データセットは問題文中の BNF で記述される文法に従う式 <expr> の 1 行のみからなり,式の文字数は記号を含めて 1000 を超えない.
Output
各データセットについて,問題文中の手順を適用した結果としてあり得る文字列のうち,辞書式順序で最初に現れるものを 1 行に出力せよ.正しい出力は空文字列にならないことが保証される.
Sample Input
6 ?(icpc) ?(?(icpc)) ?(ic)?(pc) ?(?(icp)c) ?(i?(?(c))pc) ?(bca)?(?(bca))
Output for the Sample Input
cpc cp cc cc ip bca
Problem G
連絡を絶やすな
名コンビであるふたりのエージェント A, B がアジトへの潜入ミッションを行う.アジトの警備は厳重であるため,エージェント A, B は,それぞれ確認済みの安全な潜入経路 RA, RB をたどり移動することとした.潜入経路は二次元平面上の折れ線(線分の並び)である.
各エージェントはそれぞれの潜入経路の最初の線分の開始端から潜入する.同時にふたりとも最後の線分の終端にいればミッション完了である.
ミッション中エージェントは経路上を連続的に移動するなら,自由な速度で前進も後退もでき,一時停止することもできる.しかし,ジャンプして不連続に移動することはできない.潜入経路の線分は同じ経路上の他の線分と交差したり重なったりしているかもしれないが,それを移動には利用できない.厳密には,ある線分上にいるエージェントが他の線分に移れるのは,次の場合だけである.
- 移動先が経路上で直後の線分で,エージェントが現在の線分の終端にいる場合.
- 移動先が経路上で直前の線分で,エージェントが現在の線分の開始端にいる場合.
例えば,下の図 G-1 において,潜入経路 RB の線分 3-4 から線分 4-5 に移るには,線分 3-4 の終端である (−1, 1) に移動しなければならない.また,線分 2-3 から線分 3-4 に移るときに,最後の線分の終端と同じ座標 (2, 1) を通過するが,このときは最後の線分の終端にいることにはならない.
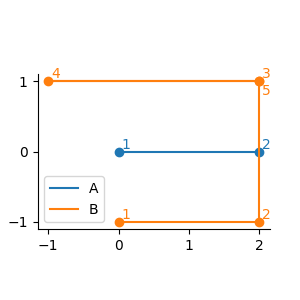
図 G-1: Sample Input の 1 番目のデータセットの潜入経路
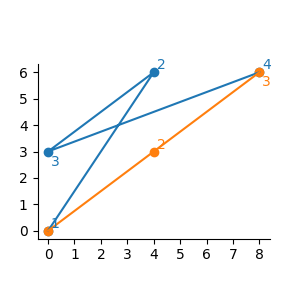
図 G-2: Sample Input の 2 番目のデータセットの潜入経路
不測の事態に備えてふたりのエージェントは無線通信機を携帯し,常にふたりの間の連絡がとれる範囲内にいなくてはならない.電波強度を上げれば通信可能な距離は長くなるが,傍受の危険性も高まる.両エージェントが適切に移動するとして,任務完了に必要な通信可能距離の最小値を求めよ.
Input
入力は複数のデータセットからなる.各データセットは次の形式で表される.
n
xA,1 yA,1
⋮
xA,n yA,n
m
xB,1 yB,1
⋮
xB,m yB,m
n は潜入経路 RA を構成する折れ線の頂点数を表す.n は 2 以上 40 以下の整数である.
xA,i と yA,i (1 ≤ i ≤ n) は i 番目の頂点の座標を表す.xA,i と yA,i はそれぞれ −1000 ≤ xA,i ≤ 1000, −1000 ≤ yA,i ≤ 1000 を満たす整数である.1 ≤ i ≤ n−1 を満たす i について (xA,i, yA,i) が i 番目の線分の開始端,(xA,i+1, yA,i+1) が終端である.どの線分の長さも 0 ではない.すなわち,xA,i ≠ xA,i+1 と yA,i ≠ yA,i+1 の少なくとも一方は成り立つ.
m および xB,j, yB,j (1 ≤ j ≤ m) は潜入経路 RB の情報を表す.形式および制約は RA についてのものと同じである.
入力の終わりは,ゼロだけからなる行で表される.データセットの個数は 50 を超えない.
Output
各データセットについて,任務中のエージェント間の距離の最大値が最小になるようにふたりが移動するとき,ふたりの間の距離の最大値を 1 行に出力せよ.出力は相対誤差または絶対誤差が 10−8 以下であれば許容される.
Sample Input
2 0 0 2 0 5 0 -1 2 -1 2 1 -1 1 2 1 4 0 0 4 6 0 3 8 6 3 0 0 4 3 8 6 10 40 15 40 20 40 15 45 10 50 12 50 10 50 15 60 15 65 20 70 18 10 40 10 40 15 45 20 50 18 50 15 50 20 60 20 60 15 65 10 70 12 0
Output for the Sample Input
1.414213562373 2.400000000000 9.284766908853
Problem H
芸術家の苦悩
芸術家であるあなたは,作品の材料として多くのボールとそれらを結ぶための紐を用意した.ボールには順に番号を振っていくが,最初はボールのひとつを 1 番とするだけである.他のボールはまだ番号を振っていないし,どのボールも紐で結んでいない.
作品制作には以下の操作のどちらかを行うことを繰り返す.
- 複製:
- 制作途中の作品のレプリカを作る.これまでに番号付けしたボールが n 個あるとき,まだ番号のついていないボール n 個に n+1, ..., 2n という番号を振る.これで 2n 個のボールに 1 から 2n の重複しない番号を振ったことになる.次に,複製前に直接結ばれていたふたつのボールの組すべてについて,それが u 番と v 番なら,新たに n+u 番と n+v 番のふたつのボールを紐で結ぶ.
- 新たな結合:
- 番号がついているふたつの異なるボールを選び,紐で結ぶ.ただし,ふたつのボールが既に直接結ばれていたら何もしない.
最初はひとつのボールにしか番号がついていないので,まずは複製から始めることになる.
図 H-1 に Sample Input の 2 番目のデータセットの作品の制作過程を示す.
図 H-1: 作品の制作例
すべての真の芸術家と同様完璧主義者であるあなたは,不完全な作品には我慢できない.不満足な作品は,つないだ紐を全部引きちぎって一刻も早く完全に破壊してしまいたい.そこで,あなたは番号のついたボールのうちのいくつかを片手に,残り全てをもう一方の手に持って,ふたつの端点が左右の手にまたがるような紐を全部いっぺんに引きちぎることにした.この行為を 1 回だけ行うことでボールとボールを結ぶ紐を全て切断できれば,作品の破壊は成功である.逆に,同じ手に持ったボール同士を結ぶ紐があるようならば,それが切断されずに残ってしまうので,作品の破壊は失敗である.
図 H-2 は Sample Input の 2 番目のデータセットで作られる作品の破壊を試みる様子を示している.この作品を破壊するには,どちらの手にも 3 個以上のボールを持つ必要がある.
図 H-2: 上述の作品の破壊
与えられた操作の列によって作られる作品について,上記のやり方でこれを破壊できるか判定せよ.できる場合は,少なくともいくつのボールを左手に持つ必要があるか求めよ.右手にはいくつのボールを持ってもよい.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
m
a1
⋮
am
m はあなたが行った操作の数を表す.m は正の整数であり,300 を超えない.
i 番目の操作 ai (i = 1, ..., m) は以下のいずれかの形式で与えられる.
COPY-
これは問題文中の 複製 操作を表す.単一のデータセットに含まれる
COPY操作の総数は 60 を超えないことが保証される. LINKu v- これは問題文中の 新たな結合 操作を表す.この操作では,番号 u, v の 2 個のボールを確認し,これらがまだ直接結ばれていなければ紐で結んだ.u と v は u < v を満たす正の整数で,この操作の時点で番号 u, v のボールがそれぞれ存在することが保証される.
入力の終わりは,ゼロだけからなる行で表される.入力に含まれるデータセットは 100 個以下である.
Output
各データセットについて,ひとつの整数からなる行を出力する.上述の方法で作品を破壊することができるならば,そのとき左手に持つ必要があるボールの最小の個数を出力せよ.作品の破壊が不可能ならば −1 を出力せよ.
Sample Input
3 COPY LINK 1 2 COPY 8 COPY COPY LINK 1 2 LINK 1 3 LINK 1 3 COPY LINK 5 6 LINK 3 6 5 COPY LINK 1 2 COPY LINK 1 3 LINK 2 3 2 COPY COPY 0
Output for the Sample Input
2 3 -1 0
