ICPC 2024 アジア地区横浜大会国内予選解説

Links

Problem A

おやつは 300 円以内

提案：稲葉一浩
主担当：稲葉一浩

与えられた整数の列を for 文などを使って先頭から順に見て，それまでに加えた値の和が 300 を超えなければ加え，超えるようであれば何もせず次に進む，というプログラムを実装するとよい．題意に沿って素直に実装すると入力データのサイズに比例する時間で計算が終わるので，計算量に関する特別な工夫などは必要ない．

Problem B

追い抜き

提案：石畑清
主担当：石畑清

1 分ごとに 2 人の選手が走った距離を与えられたとき，両者あわせて何回の追い抜きがあったかを求める問題である．

1 分ごとのタイミングで，どちらがリードしているかを判断するのは簡単である．問題はその前にどちらがリードしていたかの判断である．2 つの方法が考えられる．

どちらがリードしていたかを記録する変数を順次更新していく．この変数の値は，A がリード，B がリード，まだどちらもリードしたことがない、の 3 種類とする．両者の通算の距離が同じであれば，変数の値を書き換えず，その前の値のままとするのがポイントである．この方法なら n に比例する計算時間で済む．
走行距離の記録を過去に向かって遡り，最後にどちらかがリードしていたタイミングを探す。最悪の場合は n² に比例する時間がかかるが，n の上限は 1000 なので，この方法でも十分である．

Problem C

ハチの巣距離

提案：山口文彦
主担当：山口文彦

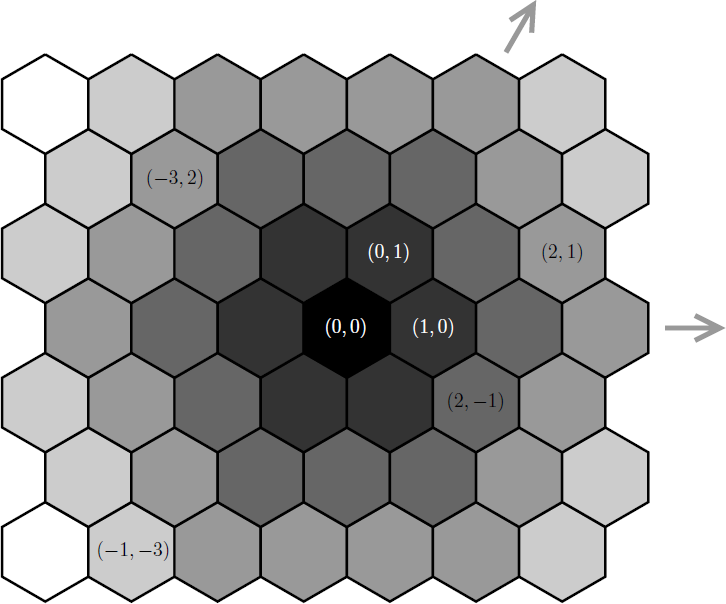
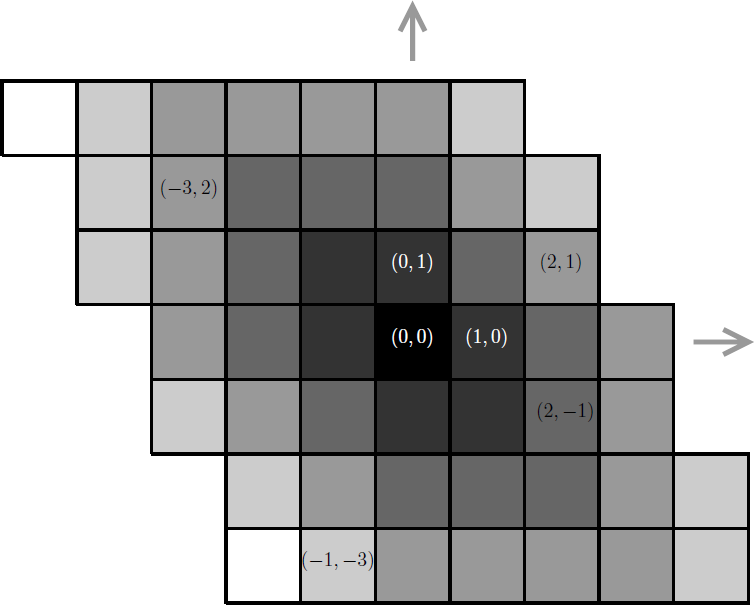
移動回数の最小値を求める問題ではあるが，問題の空間が均質なので，探索をする必要はない． y 軸が傾いた斜交座標系のような番号付けが与えられているが，これを見慣れた直交座標系で考えてみるとイメージしやすいだろうか．

x と y の符号が同じ場合 (第 1・3 象限) と異なる場合 (第 2・4 象限) で，様子が違うことが分かる．符号が同じ場合は，|x| 回の移動で指定したマスと x 座標を合わせ，|y| 回の移動で y 座標を合わせることができる．

符号が異なる場合，左上へ移動することで x が減り y が増える（右下に移動する場合は，この逆）．左上または右下へ min(|x|, |y|) 回移動すれば，x 座標かまたは y 座標の一方を指定したマスと合わせることができる．残る y または x の差は max(|x|, |y|) − min(|x|, |y|) であるから，これらの合計が最小の移動回数となる．

まとめると，(0, 0) から (x, y) までのハチの巣距離は， x と y の符号が同じであれば |x| + |y| であり，異なれば max(|x|, |y|) となる．

Problem D

だんごむしではないむし

提案：楠本充
主担当：楠本充

この問題では移動距離 d が非常に大きいので単に 1 ステップずつシミュレーションするのでは計算が間に合わない．高速化する必要がある．

まず，移動中に虫の x または y 座標が 0 未満か 101 以上になった場合には，そこから未来永劫，虫が障害物に出会うことは無い．この場合にはそのときの座標から，残りの移動距離分だけ向きに沿って虫を直線移動をさせれば答えが求まる．

そのようにならない場合を考える．虫の x, y 座標が 0 以上か 100 以下であるときの虫の状態は，向きが 4 方向あることを考慮して高々 101 × 101 × 4 通りである．虫の移動を初期状態から 1 ステップずつシミュレーションして過去と同じ状態になった場合，虫は今後もその状態からある一定の状態遷移をずっと繰り返すことになる．この繰り返しの移動距離の長さを c とすると，残りの移動距離を c で割った余りを取ることにより，シミュレーションの残りのステップを高々 c 以下にできる．c は 101 × 101 × 4 以下であり小さいため，再び 1 ステップずつシミュレーションしていけば答えが求まる．

以上の 2 つの考察を踏まえることで，(101 × 101 × 4 + n) に比例する程度の計算時間でこの問題を解くことができる．

余談であるが，だんごむしには交替性転向反応と呼ばれる移動メカニズムがあるようである．この移動メカニズムは本問題中の虫がやっていることよりも複雑である．

Problem E

カラフルな住宅街

提案：佐藤遼太郎
主担当：丸茂直貴

c₁ = c_n の場合は，土地の外周に家を配置することで目標が達成できる．以下では c₁ ≠ c_n の場合を考える．

最も南の行に注目する．西から見たとき最も右の色が c_n であるという条件と，東から見たとき最も左の色が c₁ であるという条件から，目標達成のためには 1 ≤ i < j ≤ n を満たすある i, j に対し，a_n,i = c_n かつ a_n,j = c₁ である必要がある．これは下図のような状況である．

土地を南から見ることも考えると，前述の i, j に対し，c_i = c_n, c_j = c₁ が成り立つ必要がある．すなわち，3 条件 1 < i < j < n, c_i = c_n, c_j = c₁ を満たす i, j が存在しない場合の答えは No である．

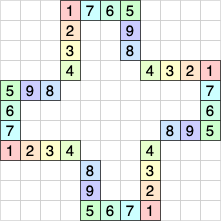
このような i, j が存在する場合は，例えば以下の図のように家を配置し色を塗れば，目標を達成することができる．

Problem F

ビリヤード

提案：住谷達哉
主担当：鵜川始陽

ビリヤード台上の球を一つだけ直線状に撃ち出して，コインがある座標を狙う問題である．球は壁に当たると跳ね返る．止まっている球に当たったり台の隅の穴に落ちることなくコインに当たる球を探すことが求められている．

それぞれの球の動きをシミュレーションするか，コインに当たった球があると仮定してその球の動きをコイン側からシミュレーションする．球の数が多いので，これをどうまとめて球との衝突判定を軽くするかが鍵となる．球の軌道は直線 y = x + k₁ と直線 y = − x + k₂ の上の線分を組合わせたものになる．ここで − a < k₁ < b, 0 < k₂ < a + b である．全ての球をこのうちのどの直線上にあるかで分類することで，1 回跳ね返るたびに 1 回の検査で軌道上に止まっている球があるかどうかを判定できる．

なお，全ての球の動きをシミュレーションしても，軌道の線分が存在できる直線が 2(a + b - 1) 個しかないので現実的な時間で計算が終わる．

Problem G

二組のカードセット

提案：住谷達哉
主担当：住谷達哉

赤いカード上の整数と青いカード上の整数は多重集合として一致することから，b_i = a_{p_i} (i = 1, ... n) が成り立つような 1 から n の順列 p = (p₁, p₂, ..., p_n) が存在する．各参加者に配られた 2 枚のカードに書かれた整数の和の条件 a_i + a_{p_i} = s_i は順列 p のサイクルごとに独立した連立方程式になる．

長さ k のサイクルがある場合を考える．表記の簡単のため，1 → 2 → … → k → 1 のサイクルを仮定すると，

₁

₂

₁

₂

₃

₂

a_k

₁

s_k

という連立方程式が得られる．この連立方程式が整数解を持つかの判定は k の偶奇に応じて次のように行える．

k が奇数のとき

2a₁ = s₁ − s₂ + … + s_k と解ける．a₁ が整数であることはこの式の右辺が偶数であること，すなわち s₁, s₂, ..., s_k の総和が偶数であることと同値である．また，このとき a₂ 以降も全て整数になる．

k が偶数のとき

奇数番目の式の総和と偶数番目の式の総和を比較することで，s₁ + s₃ + … + s_k−1 = s₂ + s₄ + … + s_k という条件が得られる．この条件が成り立つ場合のみ解が存在し，特に a₁ を自由に選んだ解が存在することから，整数解も存在する．

本題の解説に戻る．s = (s₁, s₂, ..., s_n) の総和が奇数のときは明らかに不可である．以下，そうでない場合を考える．

s が 1 個以上の偶数を含むとき

s の n 項を，それぞれの総和が偶数になるように奇数個の要素を持ついくつかのグループに分けることが可能である．そのグループごとのサイクルを持つような順列 p を選ぶことで整数解が得られる．

s が奇数のみからなるとき

奇数個の要素の和が必ず奇数になるため，順列 p に奇数長のサイクルがあると整数解が存在しない．そのため偶数長のサイクルのみにする必要がある．上記議論より，整数解を持つには {1, 2, ..., n} の部分集合 T であって次の条件を満たすものが必要となることが分かる．

|T| = n / 2
∑_i∈T s_i = ∑_i∉T s_i

このような T が存在するかの判定および構築は O(n³(max(s) − min(s))) の DP で実現できる．存在する場合は T の要素とそれ以外が交互に並ぶようなサイクルを持つ p を選べばよい．

Problem H

とおせんぼ

提案：佐藤遼太郎
主担当：岩田陽一

この解説中では座標は 0-indexed で表記し、行方向を x 軸、列方向を y 軸とする。ピースの配置を、ピースに属する正方形の x 座標の最小値と y 座標の最小値の組によって表すことにする。ピースの高さを h、幅を w とすると、初期位置は (0,0) であり、目標位置は (r-h,c-w) である。

あるマスを侵入禁止にすると、ピースの配置のうちの幾つかが禁止される。いくつかのマスを侵入禁止にしたことで禁止されたピース配置が、初期位置の (0,0) と目標位置の (r-h,c-w) を分断すると、Bob の目標が達成される。盤面の平面性からこの条件は、左下側(x=r-h or y=0)から右上側(x=0 or y=c-w)へ禁止された配置を８方向に辿るパスが存在する、と言い換えることができる。

あるマスを侵入禁止にしたとき、禁止されるピース配置は、ピースを180度回転させて[0,r-h]×[0,c-w]の長方形との共通部分をとったものとなる。ピースの形状に関する制約から、この図形は常に連結である。従って、先の言い換えにおける禁止された配置を辿るパスは、この禁止された連結な図形を順に辿っていくもののみを考えれば十分である。よって、最短路問題に帰着してこの問題を解くことができる。

ピースの大きさを n とすると、頂点数 O(rc)、辺数 O(rcn) のグラフの最短路問題に帰着されるため、全体の計算量は O(rcn log rc) となる。最短路問題への帰着方法によっては辺数が O(rcn^2)となるものもあるが、制約的にはこちらでも実行時間制限には間に合うと想定される。

Problem I

全員生還?

提案：城下慎也
主担当：城下慎也

この問題は最適な攻撃対象を選択することで，味方チームの誰の風船も割られない確率を最小化する問題である．

どの味方よりも先に攻撃する敵およびどの敵よりも後に攻撃する味方は攻撃対象の選択に影響を与えないため取り除いておく．すると，行動順は「味方の行動が連続する区間（味方区間）」と「敵の行動が連続する区間（敵区間）」が交互に現れる．

末端の敵区間から後ろ向きに確率を計算することを考える．

味方区間と敵区間が 1 個ずつの場合，味方が狙う敵は常に「まだ攻撃できる敵のうち命中率が高い順」に狙うことが最適となる．このときの味方の風船がすべて残る確率を $R(0)$ とする．

先ほどの味方区間よりも前に，追加で $k$ 回の攻撃が敵区間に対し行われ成功するとする．このときの追加攻撃の最適解も「まだ攻撃できる敵のうち命中率が高い順」である。このときの味方の風船がすべて残る確率を $R(k)$ とする．

味方区間と敵区間が 2 個ずつの場合，最初の味方区間では直後の敵区間を直接狙う代わりに，先の敵区間を狙うことも可能である．ここで，「2 番目の味方区間と敵区間全体」は，敵の数を $m$ 人としたとき，「命中率が $1 - R(0) / R(1), 1 - R(1) / R(2), ... 1 - R(m-1) / R(m)$ の敵からなる敵区間」に置き換えても最適解が変わらない（※）．すると，敵と味方の区間が 1 個ずつの場合と同様に解くことができる．

味方区間と敵区間が 3 個以上の場合も再帰的にマージすることで解くことができる．

以下，（※）を示す．（※）は以下の 2 種類の命題に分解することができ，それぞれを敵区間数の帰納法によって示す．

命題 1: 敵全体の集合に対しある順列（「グローバルな攻撃順」と呼ぶ）が定義でき、「まだ行動可能な敵のうちグローバルな攻撃順で最優先の目標を貪欲に狙う」戦略で最適解を得ることができる．

命題 2: 現在の区間集合全体に対し、「事前に $x$ 人敵を選択して倒すことができるとしたときの最大勝率」を $R(x)$ とする．このとき、$R(x)$ はある実数列 $d_1 \le d_2 \le ... \le d_n$ を用いて次のように記述することができる．

$$ \begin{align} R(0) & = & d_1 * d_2 * d_3 * ... * d_n\\ R(1) & = & d_2 * d_3 * ... * d_n\\ R(2) & = & d_3 * ... * d_n\\ & : & \end{align} $$

◯ 敵区間数が 1 個の場合

もし，味方のうち誰が成功し誰が失敗するかが事前にわかっている場合は，敵の命中率の高い順（同じ命中率なら左優先とする）に選ぶことが最適である．攻撃対象の決定前に味方の命中可否がわかっていない場合も，命中率の高い敵から貪欲に狙うことで同じ成功率を達成できる．これは，貪欲に狙った場合は実際に誰が成功したかによらず最終的に命中率の高い順に行動不能になっていることから示せる．すなわち，命中率の高い順にグローバルな攻撃順を定義することで命題 1 が成立する．命題 2 についても，敵の命中率を高い順に $p_1, p_2, ...$ としたとき，$d_i = 1 - p_i$ とすることで成立する．

◯ 敵区間数が $k$ 個以下でグローバルな攻撃順が定義できるとしたときの，敵区間数が $k+1$ 個の場合

まず，命題 1 を示す．まず，全体は「$k+1$ 番目の味方区間」「$k+1$ 番目の敵区間」「$k$ 番目以下の区間」に分解できる．

「$k+1$ 番目の敵区間」と「$k$ 番目以下の区間」は帰納法の仮定よりそれぞれにグローバルな攻撃順を定義できる．両者を結合した全体でグローバルな攻撃順を定義できるか考える．

「$k+1$ 番目の味方区間」での命中成否が事前に分かっているとする．「$k+1$ 番目の敵区間」に $a$ 回，「$k$ 番目以下の区間」に $b$ 回攻撃を命中させるとき，それぞれの区間でそれぞれのグローバルな攻撃順に従って攻撃することが最適となる．全体でグローバルな攻撃順が定義できるためには，$a + b + 1$ 人倒せるときの最適解が，$a + b$ 人倒せるときの最適解に 1 人加えることで実現できることを示せばよい．

帰納法の仮定より、「$k+1$ 番目の敵区間」「$k$ 番目以下の区間」それぞれについて前述の $R$ を定義したとき，それぞれの実数列 $d_{l,1} \le d_{l,2} \le ... \le d_{l,m}$ および $d_{r,1} \le d_{r,2} \le ... \le d_{r,m}$ が定義できる．すると、a+b+1 人倒せるときの最適解は、${d_{l,1}, d_{l,2}, ... d_{l,m}, d_{r,1}, d_{r,2}, ... d_{r,n}}$ 全体の集合のうち，小さい方から $a+b+1$ 番目までを選べばよい．選び方より，この集合の中に $a+b$ 人倒せるときの最適解が含まれている．

味方の命中可否がわからない場合も先程と同様の議論で貪欲法の最適性が示せる．

最後に命題 2 を証明する．${d_{l,1}, d_{l,2}, ... d_{l,m}, d_{r,1}, d_{r,2}, ... d_{r,n}}$ 全体を昇順に並べ替えた順列を $(d'_1, d'_2, ...)$ とする．「$k+1$ 番目の味方区間」が 0 人のときは，最大勝率 $R(x)$ は $R(x) = Π_{x \lt y} d'_y $ となり条件を満たす．「$k+1$ 番目の味方区間」が $r (\ge 0)$ 人で成立している状態から、命中率 $p$ の味方が「$k+1$ 番目の味方区間」の末端に増えたときを考える．

新しい味方が増える前の最大勝率 $R(x)$ が計算されており，条件を満たしているとする．新しい味方が増えたときの最大勝率 $R'(x)$ は，

$$ R'(x) = p * R(x - 1) + (1 - p) * R(x) $$

となる．このとき，

$$ \begin{eqnarray} R'(x + 1) * R'(x - 1) - R'(x)^2 & = & (p * R(x) + (1 - p) * R(x + 1)) * (p * R(x - 2) + (1 - p) * R(x - 1))\\ & & - (p * R(x - 1) + (1 - p) * R(x)) * (p * R(x - 1) + (1 - p) * R(x))\\ & = & p^2 (R(x)R(x-2) - R(x-1)^2) + (1-p)p(R(x-2)R(x+1) - R(x-1)R(x)) \\ & & + (1-p)^2(R(x+1)R(x-1) - R(x)^2)\\ & \le & 0 \end{eqnarray} $$

($R(x)$ の定義より $x \le y$ なら $R(x-1)/R(x) \le R(y)/R(y+1) \Leftrightarrow R(x)R(y) \ge R(x-1)R(y+1)$)

が言えるため，$d_x = R'(x - 1) / R'(x) \le R'(x) / R'(x + 1) = d_{x+1}$ が成り立つ．これを再帰的に定義することで任意の長さの「$k+1$ 番目の味方区間」についても命題 2 が成り立つ．

全体で $O(n^2)$ で解くことができる．実装方針によっては，命中率 1 の敵の扱いに注意する必要がある．