Links
Problem A
おやつは 300 円以内
あなたの友人の貪欲太郎君は,遠足のおやつを買いに,300 円を握りしめて駄菓子屋に出かけた. 駄菓子屋の棚には各商品が 1 つずつ横 1 列に並べられている. 駄菓子屋に入ると彼は買い物かごを手に取り,棚の商品を左から順に見ていく. おやつが好きすぎる彼は,見た商品をかごに入れても合計が 300 円を超えないようであれば,すぐにかごに入れてしまう. 合計が 300 円を超えてしまうようなら,その商品は泣く泣くあきらめるのである. このようにして右端まで見終わると,レジに向かい,かごに入った商品を購入する.
駄菓子屋の商品の値段のリストが与えられるので,貪欲太郎君はいくらお金を使うことになるか求めて欲しい.
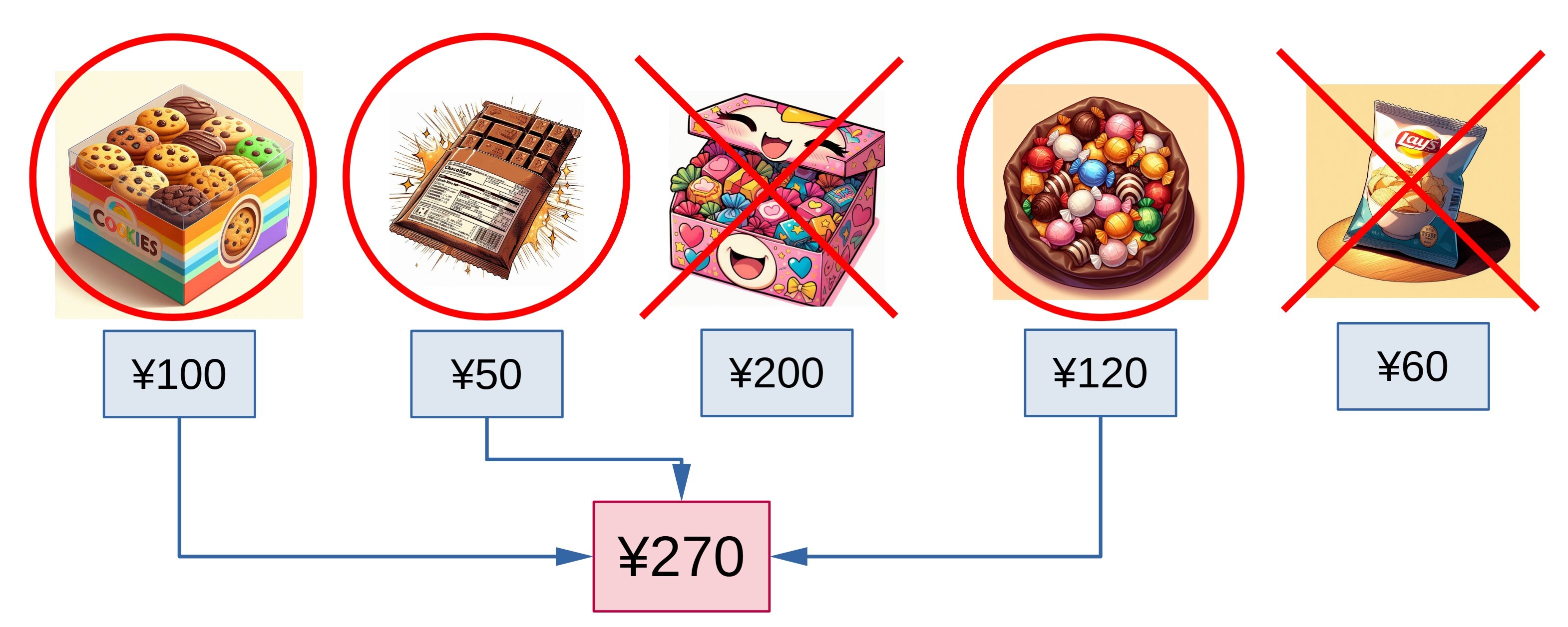
図 A-1: Sample Input の最初のデータセット
Input
入力は複数のデータセットからなる.データセットの個数は 50 を超えない. 各データセットは次の形式で表される.
n
a1 a2 ⋯ an
n は駄菓子屋の商品の数を表す 1 以上 100 以下の整数である. ak (k = 1, …, n) は,1000 以下の正の整数であり,左から k 番目の商品の値段が ak 円であることを表す.
入力の終わりは,ゼロ 1 つだけからなる行で表される.
Output
各データセットについて,貪欲太郎君が何円分のおやつを買うことになるかを 1 行に出力せよ.
Sample Input
5 100 50 200 120 60 4 120 240 180 1 2 500 1000 6 2 3 5 7 11 13 0
Output for the Sample Input
270 300 0 41
Problem B
追い抜き
2 人の選手が長距離走レースを行う.ただし,その方式は普通の陸上競技と違っている.すなわち,決まった時間走って,どちらがより長い距離を走ったかを競う.スタート後 1 分ごとに,両者が直前の 1 分間に走った距離を記録する.レースの記録が与えられたとき,両者あわせて何回の追い抜きがあったかを求めるプログラムを書いてほしい.距離を記録するどの 1 分間も,両者とも一定のスピードを保つと仮定せよ.
追い抜きとは,リードされていた側が逆にリードすることを言う.追い抜く前に,しばらく並走する(どちらもリードしていない)状態があってもよいことに注意せよ.図 B-1 は,Sample Input の 3 番目のデータセットの各時刻の 2 人の選手の位置を図示したものである.この例の追い抜き回数は 2 である.
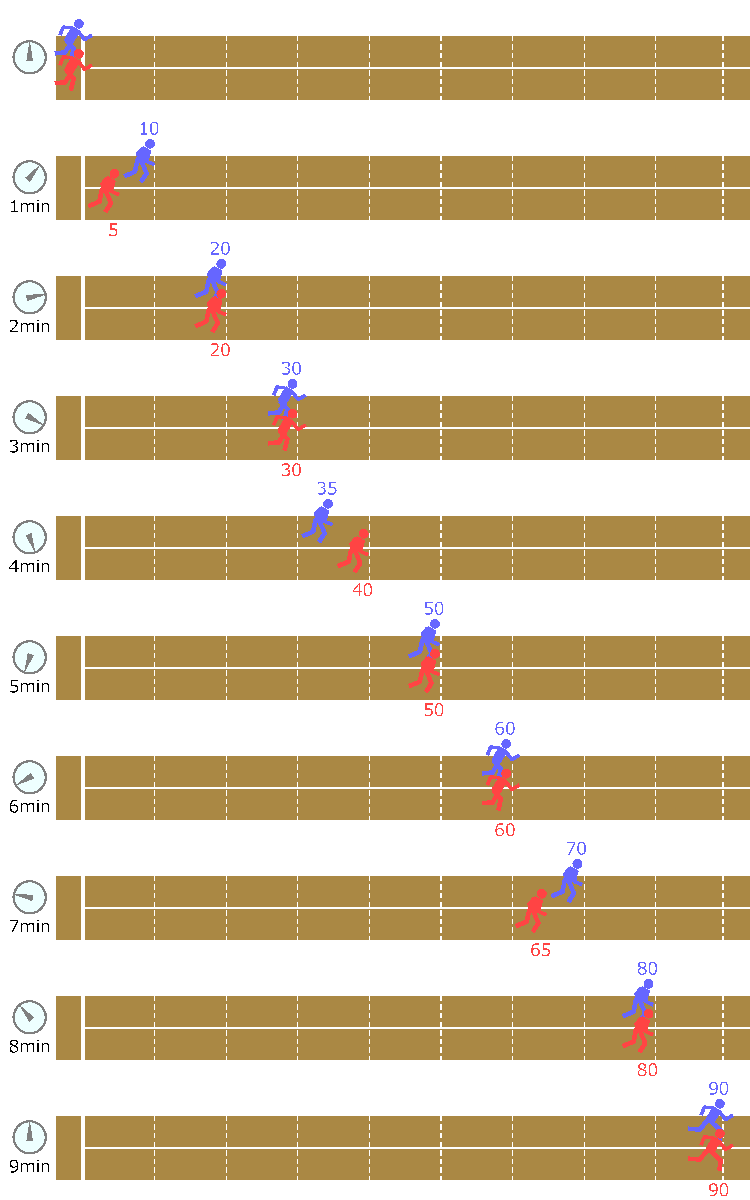
図 B-1: Sample Input の 3 番目のデータセット
Input
入力は複数のデータセットからなる.各データセットは次の形式で表される.
n
a1 ⋯ an
b1 ⋯ bn
n は,2 以上 1000 以下の整数であり,レース全体の時間を分単位で表す.各 ak (k = 1, …, n) は,1 以上 1000 以下の整数であり,1 人目の選手がスタート後 k − 1 分から k 分までの間に走った距離をメートル単位で表す.bk (k = 1, …, n) は,同様に 2 人目の選手が走った距離を表す.
入力の終わりは,ゼロ 1 つだけからなる行で表される.入力中のデータセットの個数は 100 を超えない.
Output
各データセットについて,追い抜きの回数を 1 行に出力せよ.
Sample Input
3 5 15 5 10 5 15 9 10 10 10 10 10 10 10 10 10 5 15 10 5 15 10 5 15 10 9 10 10 10 5 15 10 10 10 10 5 15 10 10 10 10 5 15 10 0
Output for the Sample Input
2 0 2
Problem C
ハチの巣距離
正六角形が敷き詰められた平面がある.六角形の 1 つ 1 つをマスと呼び,あるマスから 1 ステップで,辺で接するマスへ移動できる.中央のマスから指定されたマスに移動するには,少なくとも何ステップ必要であるかを求めたい.
マスの指定のために,各マスを 2 つの整数の組で表す.中央のマスは (0, 0) である.マスの辺に垂直な向きの 1 つを右向きとし,各マス (x, y) について,右隣のマスが (x + 1, y),右上隣のマスが (x, y + 1) である(下図参照).
2 つの整数 x, y が与えられたとき,マス (0, 0) からマス (x, y) まで移動するために必要なステップ数の最小値を求めるプログラムを書きなさい.
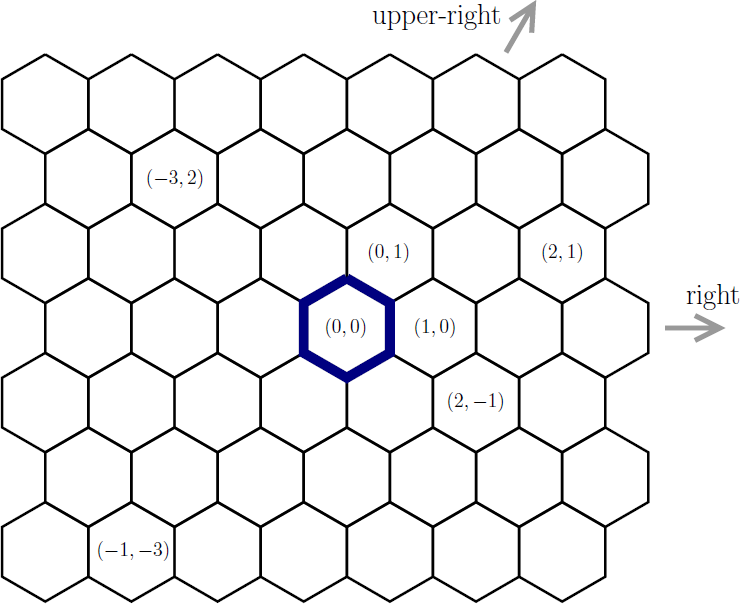
図 C-1: マスの指定方法
Input
入力の 1 行目はデータセットの個数を表す正の整数 n のみからなり,n は 100 を超えない.続く n 行の各行に 1 つずつデータセットが与えられる.
各データセットは,2 つの整数 x と y からなる.(x, y) が行き先のマスであり,−1000 ≤ x ≤ 1000 かつ −1000 ≤ y ≤ 1000 を満たす.
Output
各データセットについて,マス (0, 0) から行き先のマスまで移動するために必要なステップ数の最小値を 1 行に出力しなさい.
Sample Input
7 0 0 0 1 1 0 2 1 2 -1 -3 2 -1 -3
Output for the Sample Input
0 1 1 3 2 3 4
Problem D
だんごむしではないむし
だんごむしのような見た目の虫が平面上を歩いている.平面には直交座標が設定されており,x 軸は西から東に,y 軸は南から北に向いている.
いま,虫はある格子点 (x 座標と y 座標がともに整数である点) にいて,x 軸の正の向きを向いている.平面上のいくつかの格子点には障害物がある.虫は障害物を避けながら以下のルールで移動し続ける.
- 虫は現在の場所から,向いている方向の隣接する格子点に移動しようと試みる.
- その格子点に障害物がなければ,虫は向きを変えずにその格子点に進む.
- その格子点に障害物があれば,虫は位置を変えずに左方向に 90 度回転する.
虫の初期位置,障害物の配置,および虫の移動距離が与えられる.虫が与えられた距離だけ移動したときにいることになる位置を求めよ.
以下に Sample Input のいくつかのデータセットを図示する.バツ印で表している点が障害物のある点である.左図は最初の 2 つのデータセットである.これらのデータセットでは虫の初期位置は (0, 1) であり,(1, 1),(2, 1) へと移動していく.次に (3, 1) へ移動しようとするが,そこには障害物があるため,向きを y 軸の正の向きに変え,(2, 2) へと移動する.虫がたどる点を橙色の丸で表している.右図はさらに次の 2 つのデータセットを示す.

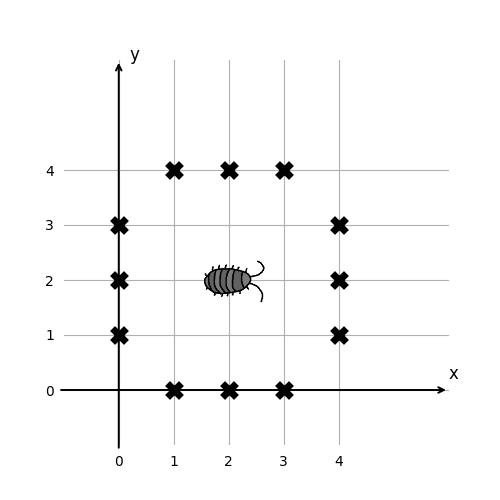
図 D-1: Sample Input の最初の 2 つのデータセット (左図) とその次の 2 つのデータセット (右図)
Input
入力は複数のデータセットからなる.データセットの個数は 200 を超えない.各データセットは次の形式で表される.
n
a b d
x1 y1
⋮
xn yn
ここで n は障害物の個数を表す整数である (1 ≤ n ≤ 1000).a と b はともに 0 以上 100 以下の整数であり,虫の初期位置は座標 (a, b) である.d は移動距離を表す整数である (1 ≤ d ≤ 1018).
i 番目の障害物は座標 (xi, yi) に存在する (i = 1, ⋯, n).xi と yi は 0 以上 100 以下の整数である.どの 2 つの障害物の位置も異なる.すなわち,i ≠ j ならば (xi, yi) ≠ (xj, yj) である.また,どの障害物の位置も虫の初期位置 (a, b) とは一致しない.与えられた配置の下で,虫は必ず距離 d 以上移動できることが保証される.
入力の終わりは,ゼロ 1 つだけからなる行で表される.
Output
各データセットについて,虫が距離 d だけ移動した後の位置の x, y 座標を表す 2 つの整数をスペース区切りで 1 行に出力せよ.
虫の位置の x, y 座標は負になり得ることに注意せよ.
Sample Input
2 0 1 4 3 1 2 5 2 0 1 9 3 1 2 5 12 2 2 11 0 1 0 2 0 3 4 1 4 2 4 3 3 4 2 4 1 4 3 0 2 0 1 0 12 2 2 7791772263873 0 1 0 2 0 3 4 1 4 2 4 3 3 4 2 4 1 4 3 0 2 0 1 0 3 0 3 198 99 2 100 3 99 4 3 0 3 1000000000000000000 99 2 100 3 99 4 1 99 100 1 100 100 0
Output for the Sample Input
2 3 -2 4 2 3 3 2 0 3 -999999999999999802 3 99 101
Problem E
カラフルな住宅街
正方形状の土地があり,東西方向・南北方向に延びる道によって n 行 n 列の正方形の区画に分けられている.
あなたはいくつかの区画に家を 1 軒ずつ建てる.各行・各列には少なくとも 1 軒建てる必要がある.さらに,各家を 1 色で塗る.使える色は色 1 から色 n までの n 色ある.
あなたはこの土地が東西南北の 4 方向からどう見えるかを気にしている.ある方向から見ると,手前にある n 軒の家が左右に並んで見える.あなたの目標は,4 つのどの方向から見ても,これらの家の色が同じ指定された順になるように,家を建てて色を塗ることである.
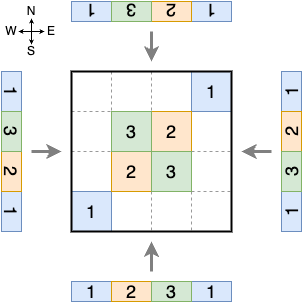
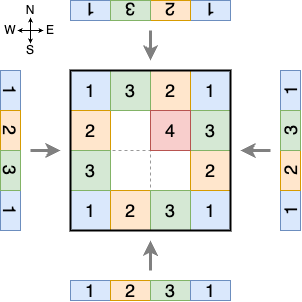
図 E-1, E-2 は,ともに n = 4 で,色の並びを左から順に 1, 2, 3, 1 と指定した場合の例である.これは Sample Input の最初のデータセットに対応する.図 E-1 の土地を南から見たとき,色の並びは 1, 2, 3, 1 となり,これは指定された並びに一致している.しかし,東から見たときは 1, 3, 2, 1 となり,指定された並びと異なる.そのため,この例では目標を達成していない.図 E-2 の例は目標を達成している.
色の並びが指定されたとき,目標を達成する家の配置と色の塗り方が存在するかを判定し,存在するならば一例を示してほしい.
Input
入力は複数のデータセットからなる.データセットの個数は 100 を超えない.各データセットは次の形式で表される.
n
c1 ⋯ cn
ここで,n は 1 以上 50 以下の整数であり,土地が n 行 n 列の区画に分けられていることと,色 1 から色 n までの n 色が使えることを表す.各 ci (i = 1, …, n) は,1 以上 n 以下の整数であり,左から i 番目の色が ci と指定されていることを表す.
入力の終わりは,ゼロ 1 つだけからなる行で表される.
Output
各データセットについて,目標を達成する家の配置と色の塗り方が存在しなければ,1 行に "No" を出力せよ.存在すれば,1 行に "Yes" を出力し,続けて目標を達成する配置の 1 つを次の形式で出力せよ.
a1,1 ⋯ a1,n
⋮
an,1 ⋯ an,n
ここで,各 ai,j (i, j = 1, …, n) は,0 以上 n 以下の整数であり,北から i 番目,西から j 番目の区画の状態を表す.ai,j = 0 の場合は,その区画に家を建てないことを表す.ai,j > 0 の場合は,その区画に家を建て,色 ai,j で塗ることを表す.
目標を達成する家の配置と色の塗り方が複数存在する場合は,そのうちのどれを出力してもよい.
Sample Input
4 1 2 3 1 4 1 2 2 1 2 1 2 0
Output for the Sample Input
Yes 1 3 2 1 2 0 4 3 3 0 0 2 1 2 3 1 Yes 0 0 0 1 0 2 0 0 0 2 2 0 1 0 0 0 No
Problem F
ビリヤード
あなたは,ビリヤードに似たゲームの懸賞に挑戦している.このゲームでは一種のビリヤード台と,同一のサイズのいくつかの球,そして景品のコイン 1 枚を使う.ビリヤード台の上には,球を跳ね返すクッションと呼ばれる弾力のある壁で囲まれた布張りの長方形の領域がある.球はその上を転がれるが,クッションで囲まれているので,球の中心が存在できるのは幅 a 奥行き b の長方形内だけである.この長方形を可動範囲と呼ぶことにする.
可動範囲の四隅の座標を (0, 0), (a, 0), (a, b), (0, b) としよう.ゲームを始めるとき,すべての球とコインは台上に,中心が可動範囲の内側の(端ではない)相異なる格子点にあるように置かれている.球やコインは十分小さいので,中心がぶつかるように動かない限り互いに接触することはない.
挑戦者は球を 1 つだけ選び,可動範囲境界の辺に対して 45 度の角度で,x 座標も y 座標も増える方向にキューを使ってその球を突く.突いた球は,可動範囲の境界に達するか,他の球に当たるか,あるいは四隅に設けた穴のどれかに落ちるまで直進する.境界に達した球は入射角と等しい反射角でクッションに跳ね返されて,また直進を続ける.他の球に当たったり,隅の穴に達して落ちてしまったら,ゲームは終了である.他の球に当たったり穴に落ちたりする前にコインに当たれば,コインを獲得できる.
どの球を突けばコインを得られるだろうか.突けばコインを得られる球を全て知りたい.
図 F-1 は Sample Input の最初と 2 番目のデータセットを図示したものである.
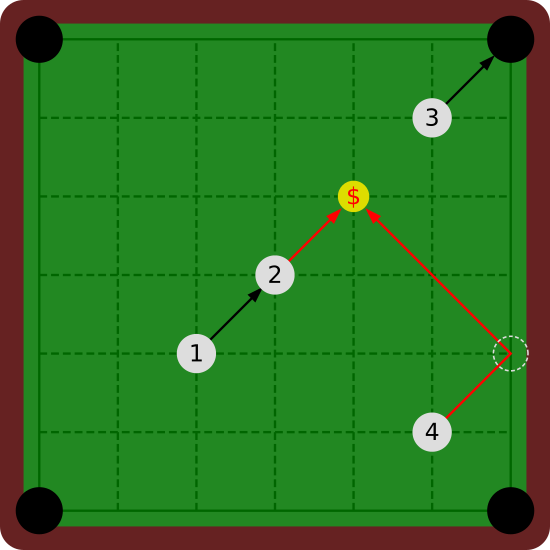
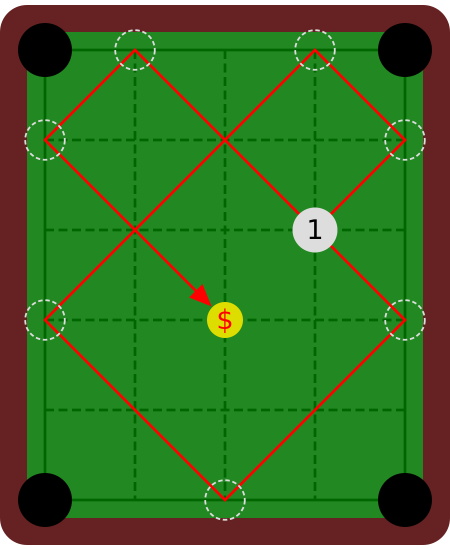
図 F-1: Sample Input の最初と 2 番目のデータセット
最初のデータセットでは,2 番の球を突けばすぐにコインに当たる.4 番の球はいったん右側のクッションで跳ね返ってからコインに当たる.1 番の球は 2 番の球に当たってしまい,3 番の球は右上隅の穴に落ちてしまうので,これらを突いてもコインを獲得できない.
2 番目のデータセットでは,唯一の球である 1 番を突くと,クッションに 5 回跳ね返されてから元の位置を通過し,さらに 2 回跳ね返されてからコインに到達する.
Input
入力は複数のデータセットからなる.各データセットは次の形式で表される.
a b x y n
x1 y1
⋮
xn yn
最初の行には 5 つの整数がある.a と b は可動範囲の幅と奥行きで,2 ≤ a ≤ 106, 2 ≤ b ≤ 106 を満たす.x と y は,コインの位置の座標 (x, y) を意味し,1 ≤ x < a, 1 ≤ y < b を満たす.n は球の数であり,1 ≤ n ≤ 105 である.
球には 1 から n までの番号が付いており,続く n 行のうち i 行目に i 番の球の座標が書かれている.この行の 2 つの整数 xi と yi は,i 番の球の中心の座標が (xi, yi) であることを意味し,1 ≤ xi < a, 1 ≤ yi < b を満たす.コインと球の位置は全て異なる.
入力の終わりは,ゼロ 5 つからなる行で表される.データセットの個数は 50 を超えない.すべてのデータセットの n の和は 5 × 105 を超えない.
Output
各データセットについて,コインを得るためにあなたが突くべき球の番号を全て,1 つの空白で区切って 1 行に出力せよ.球の番号は昇順に出力せよ.そのような球がないときは,1 行に "No" と出力せよ.
Sample Input
6 6 4 4 4 2 2 3 3 5 5 5 1 4 5 2 2 1 3 3 4 5 1 4 3 1 2 3 4 3 2 0 0 0 0 0
Output for the Sample Input
2 4 1 No
Problem G
二組のカードセット
あなたはプログラミングコンテスト後の余興として参加者のためにゲームを開催する.
ゲームには赤と青の 2 組のカードセットを用いる.どちらのカードセットも参加者数と同数のカードからなり,各カードには整数が 1 つ書かれている.また,2 組のカードセットの内容は同じであること,すなわち赤いカード上の整数と青いカード上の整数は多重集合として一致することが分かっている.しかし,各カードに実際にどんな整数が書かれているかまでは分からない.同じ色の複数のカードに同じ整数が書かれているかもしれないし,負の整数があるかもしれない.
あなたは各参加者に赤いカードと青いカードを 1 枚ずつ配った.ゲームの結果は各参加者に配られた 2 枚のカードに書かれた整数の和によって決まるので,あなたは参加者たちにこの和を申告してもらった.
参加者の申告と整合するようなカードの配り方,すなわち各参加者に配られたカードに書かれた整数の組合せとしてあり得るものを 1 つ示してほしい.ただし,参加者の計算ミスによりそのような組合せが存在しない場合もあり得る.その場合は整合する組合せが存在しないことを報告してほしい.
Input
入力は複数のデータセットからなる.データセットの個数は 100 を超えない.各データセットは次の形式で表される.
n
s1 s2 ⋯ sn
n は参加者数を表す 1 以上 70 以下の整数である.si (i = 1, …, n) は i 番目の参加者に配られた 2 枚のカードに書かれた整数の和の申告値を表す −150 以上 150 以下の整数である.
入力の終わりは,ゼロ 1 つだけからなる行で表される.
Output
各データセットについて,各参加者に配られたカードに書かれた整数の組合せとして参加者の申告と整合するものが存在しなければ,1 行に "No" を出力せよ.存在すれば,1 行に "Yes" を出力し,続けて整合する組合せとしてあり得るものの 1 つを次の形式で出力せよ.
a1 a2 ⋯ an
b1 b2 ⋯ bn
ここで,i = 1, …, n のそれぞれについて, ai と bi は i 番目の参加者に配られた赤と青のそれぞれのカードに書かれた整数を表す.ai と bi のそれぞれは −109 以上 109 以下の整数でなければならない.整合する組合せが 1 つでも存在するならば,この条件を満たすような整合する組合せも存在することが示せる.そのような組合せが複数存在する場合は,そのうちのどれを出力してもよい.
Sample Input
3 7 -2 3 3 4 8 8 4 1 2 4 8 6 -6 -2 3 2 9 -4 1 -100 0
Output for the Sample Input
Yes 1 -3 6 6 1 -3 Yes 2 4 4 2 4 4 No Yes 3 -1 4 -1 5 -9 -9 -1 -1 3 4 5 Yes -50 -50
Problem H
とおせんぼ
Alice は,単位正方形のマスからなる長方形のグリッド盤面上で,平らなピースをスライドさせて目的地まで動かすパズルで遊んでいる. 許される操作はピースの平行移動だけで,回転させたり持ち上げたりはできない. 盤面のいくつかのマスは進入禁止と指定されていて,ピースのどの部分もそのマスに入ってはならない.
ピースは,いくつかの単位正方形を辺同士でぴったり接続することで構成されている. 初期状態では,盤面の左端と上端の両方に接するようにピースが置かれている. Alice の目標は,ピースをスライドさせて盤面の右端と下端の両方に接するようにすることである.
一方,Bob はいくつかのマスを進入禁止に変更することで,Alice の目標を達成不可能にしたい. 各マスについて決められた枚数のコインを払えば進入禁止に変更できる. ただし,初期状態でピースがあるマスは進入禁止にできない. Bob が Alice の目標を達成不可能にするためには,最低何枚のコインを払う必要があるかを求めよ.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
r c
a1,1 ⋯ a1,c
⋮
ar,1 ⋯ ar,c
r と c はそれぞれ,盤面の行数と列数を表す 2 以上 100 以下の整数である. ai,j は,−1 以上 109 以下の整数であり,以下のように,行 i 列 j のマス (i, j) の状態を表す.
- ai,j = −1 の場合,初期状態でピースがそのマスを覆っている.
- ai,j = 0 の場合,最初から進入禁止である.
- ai,j > 0 の場合,Bob が ai,j 枚のコインを払うことで進入禁止にできる.
初期状態では,盤面の左端と上端の両方に辺で接するようにピースが置かれており,まだ Alice が目標を達成していないことが保証されている. すなわち,次の 2 つの条件が満たされている.
- ai,1 = −1 を満たす i と a1,j = −1 を満たす j がそれぞれ 1 つ以上存在する.
- 全ての i について ai,c ≠ −1 であるか,もしくは全ての j について ar,j ≠ −1 である.
入力の終わりは,ゼロ 2 つからなる行で表される. データセットの個数は 50 を超えない. すべてのデータセットの r の和は 1000 を超えない. すべてのデータセットの c の和は 1000 を超えない. すべてのデータセットの ai,j = −1 を満たす (i, j) の総数は 1000 を超えない.
Output
各データセットについて,Bob の支払うコインの枚数の最小値を 1 行に出力せよ.
Sample Input
3 3 -1 33 22 99 0 99 11 44 99 4 3 -1 90 10 -1 90 20 20 50 99 10 20 99 3 3 -1 33 22 99 99 99 11 44 0 3 4 99 -1 10 99 -1 -1 -1 99 99 -1 99 99 0 0
Output for the Sample Input
33 40 0 10
Problem I
全員生還?
あなたは友達と FPS ゲームで遊んでいる.このゲームでは n 人のプレイヤーが敵と味方の 2 チームに分かれて戦う.各プレイヤーの頭上には風船がついており,互いに相手チームプレイヤーの風船を割ろうとする.
各プレイヤーには行動順と呼ばれる 1 から n までの番号が振られている.また,プレイヤーごとに命中率という実数値が定められている.ゲームは n 回のフェーズからなり,i (i = 1, …, n) 番目のフェーズでは行動順 i のプレイヤー(以下,攻撃者と呼ぶ)が以下の行動を行う.
すべてのフェーズが終了したらゲームが終了する.
あなたは味方チームのプレイヤーが誰も脱落しないようにしたい.味方チームのプレイヤー全員が最適な標的選択をしたとき,ゲームの終わりまで味方が誰も脱落せずに済む確率を求めよ.ただし敵チームのプレイヤーはランダムに標的を選択するものとする.
Input
入力は複数のデータセットからなる.データセットの個数は 50 を超えない.各データセットは次の形式で表される.
n
s1 p1
⋮
sn pn
n はプレイヤーの総数であり,2 以上 300 以下の整数である.各 i (i = 1, …, n) に対し,si と pi はそれぞれ行動順 i のプレイヤーのチームと命中率を表す.si は "Ally" または "Enemy" の文字列であり,それぞれ味方チーム,敵チームに所属していることを表す.pi は 0 以上 1 以下の実数値であり,小数点以下 9 桁まで与えられる.また,どちらのチームにも必ず 1 人以上プレイヤーがいることは保証される.
入力の終わりは,ゼロ 1 つだけからなる行で表される.
Output
各データセットについて,標的を最適に選択したときに味方の誰も脱落しない確率を 1 行に出力せよ.絶対誤差または相対誤差が 10−9 以下でなければならない.
Sample Input
3 Ally 0.800000000 Enemy 0.300000000 Enemy 0.600000000 2 Enemy 0.444444444 Ally 0.111111111 5 Ally 0.500000000 Ally 0.750000000 Enemy 0.400000000 Enemy 0.100000000 Enemy 0.800000000 6 Ally 0.250000000 Ally 0.300000000 Enemy 0.200000000 Ally 0.800000000 Enemy 1.000000000 Enemy 0.750000000 10 Enemy 0.032876598 Ally 0.273941411 Ally 0.560821701 Ally 0.798896750 Enemy 0.559524781 Enemy 0.627232231 Enemy 0.864686751 Ally 0.991458997 Enemy 0.699768375 Enemy 0.675523871 0
Output for the Sample Input
0.616000000000 0.555555556000 0.621000000000 0.419750000000 0.142319776535
