Links
Problem A
Snacks within 300 Yen
Your friend, Greedy George, visits a candy store for his snacks for the school excursion, grabbing 300 yen in his hand. In the candy store, one item of each different kind of snack is placed in a line on the shelf. After entering the store, Greedy George picks up a shopping basket and starts checking the snacks on the shelf from left to right. If the sum of the prices of snacks in the basket will not exceed 300 yen, he immediately puts the checked snack into the basket. If the sum should exceed 300 yen, he tearfully skips that snack. After examining all the snacks in this manner to the right end, George heads to the checkout.
Given a list of the prices of the snacks in the store, compute how much money Greedy George will spend.
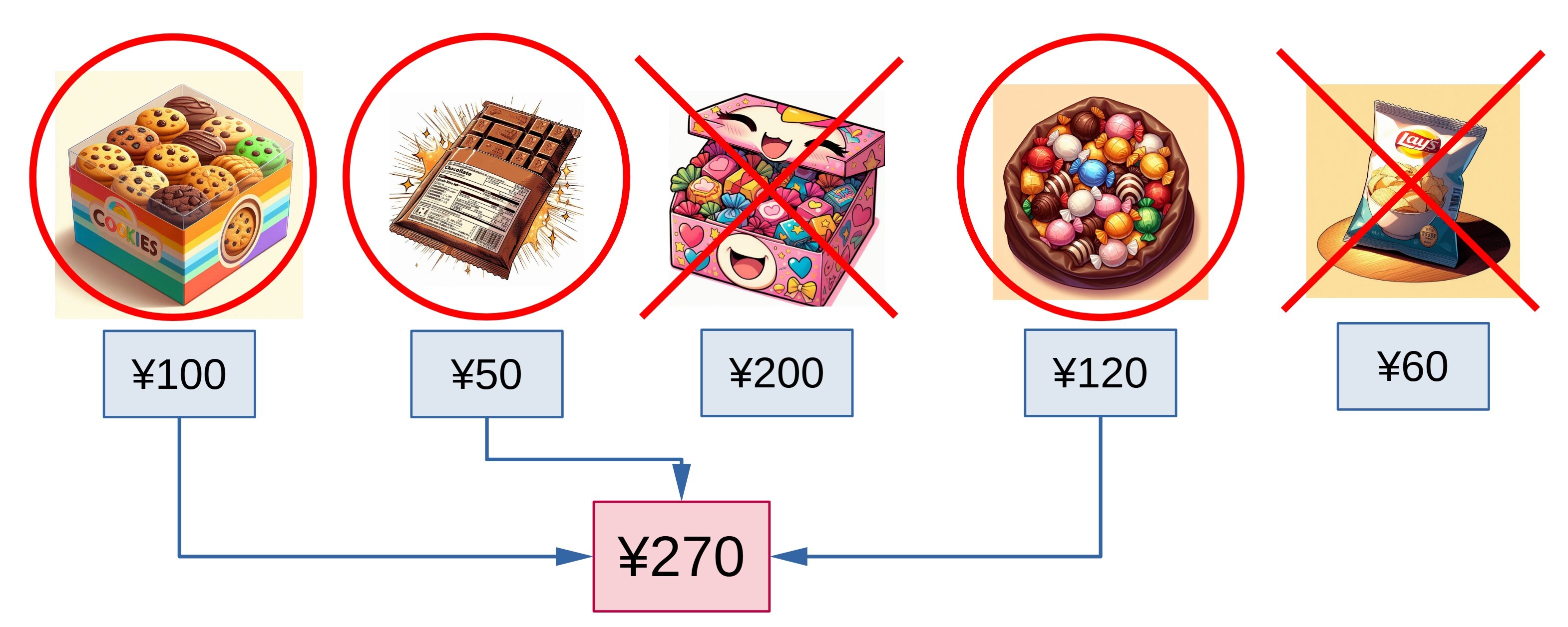
Figure A-1: The first dataset of Sample Input
Input
The input consists of multiple datasets, each in the following format. The number of datasets does not exceed 50.
n
a1 a2 ⋯ an
n (1 ≤ n ≤ 100) is the number of snacks sold in the candy store. ak (k = 1, …, n) is a positive integer less than or equal to 1000, meaning that the price of the k-th snack from the left is ak yen.
The end of the input is indicated by a line consisting of a zero.
Output
For each dataset, output in a line how many yen Greedy George will spend on the snacks.
Sample Input
5 100 50 200 120 60 4 120 240 180 1 2 500 1000 6 2 3 5 7 11 13 0
Output for the Sample Input
270 300 0 41
Problem B
Overtaking
Two athletes run a long-distance race, but the race is different from usual athletics events. They run for a predetermined duration, and the one who runs longer will be the winner. At every minute after the start, the distances both runners ran in the previous one minute are recorded. You are expected to write a program that, given the record of a race, counts the number of overtakings by either runner during the race. You should assume that both runners keep constant paces for every one minute before their distances are recorded.
Here, the term overtaking stands for the event where the runner previously behind takes the lead. Note that, before overtaking, the two runners may run side by side for a while, during which neither takes the lead. Figure B-1 shows the times and the positions of two runners for the third dataset of Sample Input. The number of overtakings in this case is two.
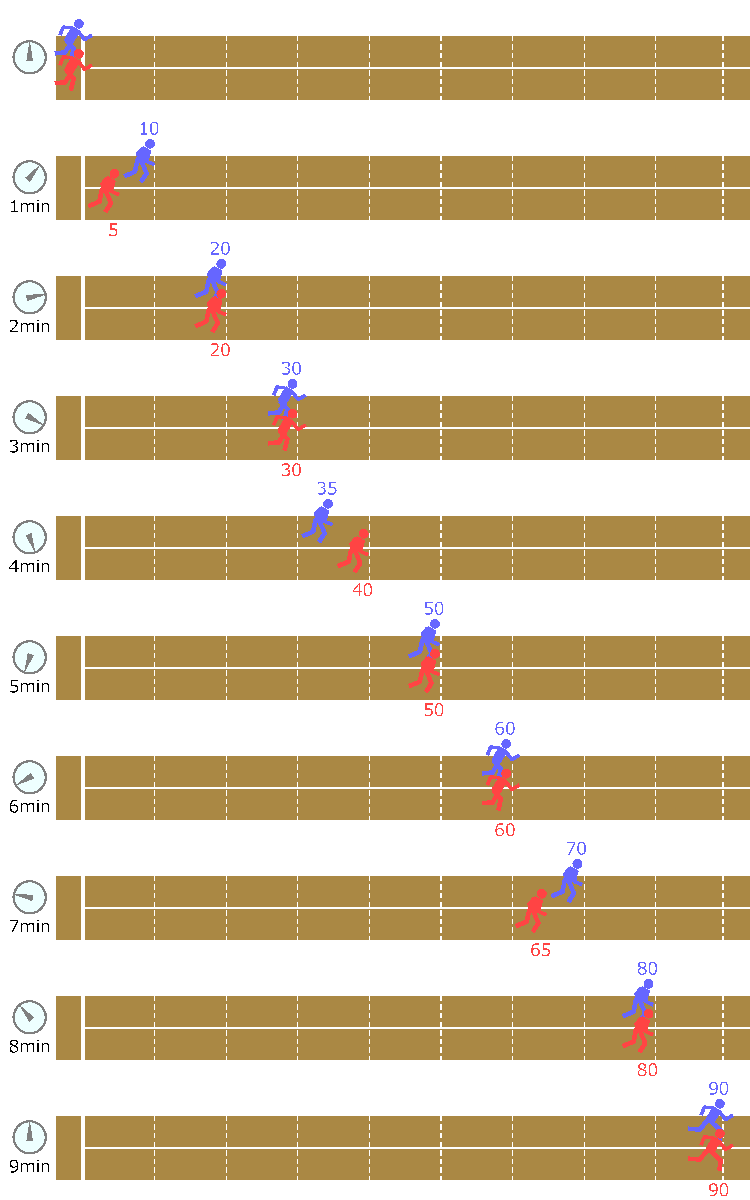
Figure B-1: The third dataset of Sample Input
Input
The input consists of multiple datasets, each in the following format.
n
a1 ⋯ an
b1 ⋯ bn
n is an integer between 2 and 1000, inclusive. It represents the duration of the race in minutes. Each of ak (k = 1, …, n) is an integer between 1 and 1000, inclusive. It represents the distance the first runner ran between k − 1 minutes and k minutes after the start of the race, in meters. Similarly, bk (k = 1, …, n) represent the distances the second runner ran.
The end of the input is indicated by a line consisting of a zero. The number of datasets does not exceed 100.
Output
For each dataset, output the number of overtakings on a line.
Sample Input
3 5 15 5 10 5 15 9 10 10 10 10 10 10 10 10 10 5 15 10 5 15 10 5 15 10 9 10 10 10 5 15 10 10 10 10 5 15 10 10 10 10 5 15 10 0
Output for the Sample Input
2 0 2
Problem C
Honeycomb Distance
A plane is tiled completely with regular hexagons. Each hexagon is called a cell. You can move in one step from a cell to one of its adjacent cells that share an edge. You want to know the minimum number of steps to move from the central cell to the specified cell.
Each cell is specified by a pair of integers. The central cell is (0, 0). One of the directions perpendicular to the edges of the regular hexagons is defined to be the rightward direction. For each cell (x, y), its right adjacent cell is (x + 1, y) and its upper-right adjacent cell is (x, y + 1). See the figure below.
Write a program that computes the minimum number of steps required to move from the cell (0, 0) to the cell (x, y) for given integers x and y.
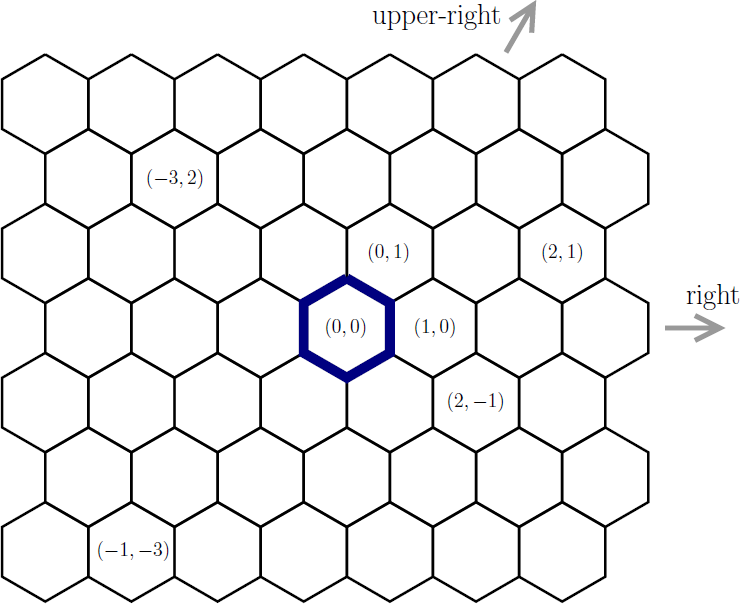
Figure C-1: How to specify the cells
Input
The first line of the input contains only one positive integer n, which is the number of datasets. n does not exceed 100. Each of the following n lines contains one dataset.
Each dataset consists of two integers x and y, which satisfy −1000 ≤ x ≤ 1000 and −1000 ≤ y ≤ 1000. The destination cell is (x, y).
Output
For each dataset, output one line containing the minimum number of steps required to move from the cell (0, 0) to the destination cell.
Sample Input
7 0 0 0 1 1 0 2 1 2 -1 -3 2 -1 -3
Output for the Sample Input
0 1 1 3 2 3 4
Problem D
A Bug That's Not a Pill Bug
A bug that looks like a pill bug is walking on a plane. A Cartesian coordinate system is defined on the plane, in which its x-axis is directed from west to east, while its y-axis is directed from south to north.
The bug is initially at a lattice point (a point where both the x- and y-coordinates are integers), facing the positive direction of x. Obstacles are placed at some of the lattice points on the plane. The bug continues to move according to the following rules, avoiding obstacles.
- The bug attempts to move from its current position to the adjacent lattice point in the direction it is currently facing.
- If that adjacent lattice point has no obstacles, the bug moves there without changing its direction.
- If that adjacent lattice point has an obstacle, the bug turns 90 degrees to the left, without changing its position.
The initial position of the bug, the locations of the obstacles, and a moving distance are given. You are requested to find the position of the bug after it has moved exactly the given distance.
Some of the datasets in Sample Input are illustrated below. The points marked with an "X" indicate the presence of obstacles. The left figure corresponds to the first two datasets of Sample Input. In these datasets, the initial position of the bug is (0, 1), and it moves to (1, 1) and then to (2, 1). Next, it attempts to move to (3, 1), but since there is an obstacle there, it turns to the positive direction of y and moves to (2, 2). The points the bug traverses are shown with orange circles. The right figure shows the next two datasets.

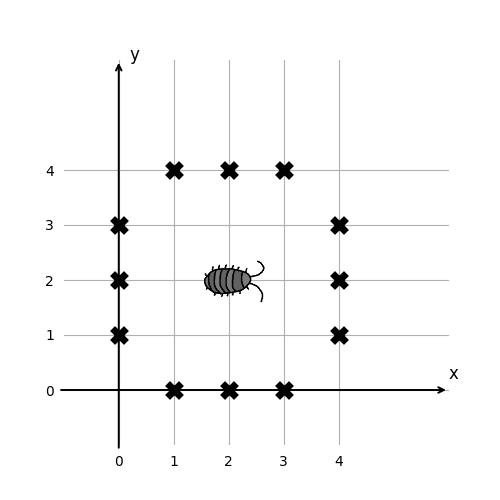
Figure D-1: The first two datasets of Sample Input (left) and the next two datasets (right)
Input
The input consists of multiple datasets, each in the following format. The number of datasets does not exceed 200.
n
a b d
x1 y1
⋮
xn yn
Here, n represents the number of obstacles, which is an integer (1 ≤ n ≤ 1000). Both a and b are integers between 0 and 100, inclusive, and the initial position of the bug is at coordinates (a, b). Additionally, d represents the distance to move, which is an integer (1 ≤ d ≤ 1018).
The i-th obstacle is located at coordinates (xi, yi) (i = 1, ⋯, n). xi and yi are integers between 0 and 100, inclusive. No two obstacles are at the same location, that is, if i ≠ j, then (xi, yi) ≠ (xj, yj). Additionally, no obstacle is located at the initial position (a, b) of the bug. It is guaranteed that the bug can move distance d or more under the given configuration.
The end of the input is indicated by a line consisting of a zero.
Output
For each dataset, output two integers separated by a space on a single line representing the x- and y-coordinates of the position of the bug after it has moved distance d.
Note that the x- and y-coordinates of the position of the bug can be negative.
Sample Input
2 0 1 4 3 1 2 5 2 0 1 9 3 1 2 5 12 2 2 11 0 1 0 2 0 3 4 1 4 2 4 3 3 4 2 4 1 4 3 0 2 0 1 0 12 2 2 7791772263873 0 1 0 2 0 3 4 1 4 2 4 3 3 4 2 4 1 4 3 0 2 0 1 0 3 0 3 198 99 2 100 3 99 4 3 0 3 1000000000000000000 99 2 100 3 99 4 1 99 100 1 100 100 0
Output for the Sample Input
2 3 -2 4 2 3 3 2 0 3 -999999999999999802 3 99 101
Problem E
Colorful Residential Area
A square-shaped plot of land is divided into n rows and n columns of square sections by streets extending in the east-west and north-south directions.
You will build one house each on some of these sections. At least one house must be built in every row and also at least one in every column. You then paint each house in one color; there are n colors available, from color 1 to color n.
You are interested in the views from four directions, north, south, east, and west. When seen from one direction, n frontmost houses can be seen, lined up from left to right. Your goal is to build and paint the houses so that the n frontmost houses seen from all the four directions are in the same specified color order.
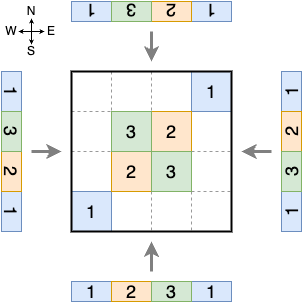
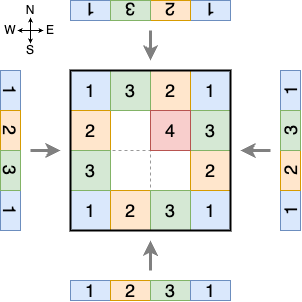
Figures E-1 and E-2 both show examples with n = 4, where the specified color order is 1, 2, 3, and 1, from left to right, which correspond to the first dataset of Sample Input. When viewing the plot in Figure E-1 from the south, the color order is 1, 2, 3, and 1, which coincides with the specified order. When viewing from the east, however, the order is 1, 3, 2, and 1, which is different. Therefore, this example does not achieve the goal. The example in Figure E-2 achieves the goal.
For the specified color order, determine whether there exists an arrangement of the positions of houses and their colors that achieves your goal, and if so, provide an example.
Input
The input consists of multiple datasets, each in the following format. The number of datasets does not exceed 100.
n
c1 ⋯ cn
Here, n is an integer between 1 and 50, inclusive, indicating that the plot is divided into n rows and n columns of sections and that n colors, from color 1 to color n, are available. Each ci (i = 1, …, n) is an integer between 1 and n, inclusive, meaning that the i-th color from the left is specified to be ci.
The end of the input is indicated by a line consisting of a zero.
Output
For each dataset, if there is no arrangement of the house positions and colors that achieves the goal, output "No" in one line. If there are one or more arrangements, output "Yes" in one line, followed by one arrangement that achieves the goal in the following format.
a1,1 ⋯ a1,n
⋮
an,1 ⋯ an,n
Here, each ai,j (i, j = 1, …, n) is an integer between 0 and n, inclusive, representing the state of the section located at the i-th row from the north and the j-th column from the west. If ai,j = 0, it indicates that no house is built on that section. If ai,j > 0, it indicates that a house is built on that section and painted with color ai,j.
If there exist multiple arrangements that achieve the goal, you may output any one of them.
Sample Input
4 1 2 3 1 4 1 2 2 1 2 1 2 0
Output for the Sample Input
Yes 1 3 2 1 2 0 4 3 3 0 0 2 1 2 3 1 Yes 0 0 0 1 0 2 0 0 0 2 2 0 1 0 0 0 No
Problem F
Billiards
You are challenging a game with prizes, which is similar to billiards. This game uses a kind of billiard table, several balls of the same size, and a prize coin. The top of the table has a flat rectangular cloth-covered area bounded by elastic bumpers, called cushions. The balls can move on this area. The cushions limit the moves so that the centers of the balls are restricted to stay within a rectangular area of width a and length b, called the movable area.
Let the coordinates of the four corners of the movable area be (0, 0), (a, 0), (a, b), and (0, b). At the start of a game, all the balls and the coin are placed on the table so that their centers are at distinct inner lattice points on the movable area, that is, not on its boundaries. As the balls and the coin are small enough, they do not touch each other unless a ball goes toward the center of another ball or the coin.
The challenger chooses one of the balls, and strikes it with a cue to the direction with an angle of 45 degrees to the edges of the boundary of the movable area. The direction is such that both x- and y-coordinates increase. The struck ball will move straight until it reaches a boundary of the movable area, hits another ball, or drops into one of the holes placed at four corners. When the ball reaches a boundary, it bounces on the cushion at the reflection angle equal to its incident angle and continues its straight move. When it hits another ball or drops into a corner hole, the game is over. If it hits the coin before hitting another ball or dropping into a hole, the challenger will win the coin.
Which ball should you strike to win the coin? You want to know all the balls bringing you the coin.
Figure F-1 depicts the first and the second datasets of Sample Input.
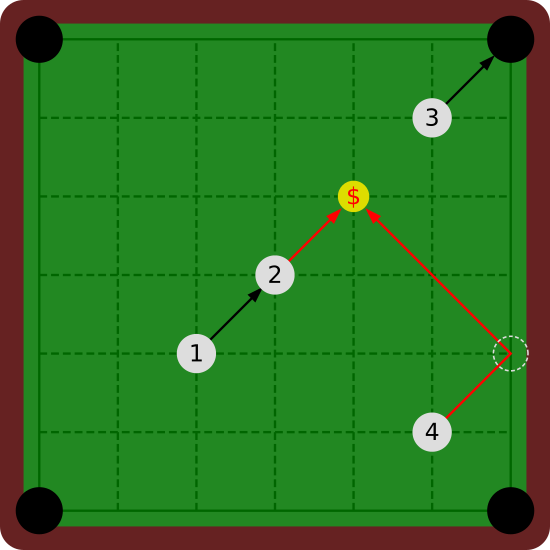
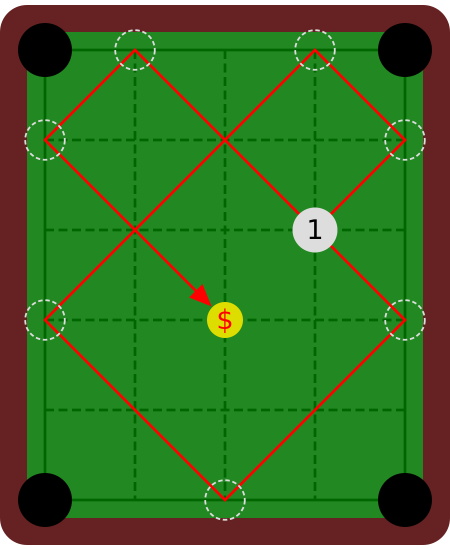
Figure F-1: The first and the second datasets of Sample Input
For the first dataset, when the ball No. 2 is struck, it goes directly toward the coin. The ball No. 4 hits the coin after bouncing on the right-side cushion. As the ball No. 1 hits the ball No. 2, and the ball No. 3 drops in the upper right hole, striking them will not be awarded a coin.
For the second dataset, when the only ball No. 1 is struck, after bouncing on the cushions 5 times, it will pass through its original position, and then after bouncing twice more, it reaches the coin.
Input
The input consists of multiple datasets, each in the following format.
a b x y n
x1 y1
⋮
xn yn
The first line has five integers. a and b are the width and the length of the movable area, respectively, satisfying 2 ≤ a ≤ 106 and 2 ≤ b ≤ 106. x and y give the coordinates (x, y) of the position of the coin, satisfying 1 ≤ x < a and 1 ≤ y < b. n is the number of balls, satisfying 1 ≤ n ≤ 105.
The balls are numbered from 1 to n, and the i-th line in the following n lines has the coordinates of the ball i. The line contains two integers xi and yi meaning that the coordinates of the center of the ball i are (xi, yi). They satisfy 1 ≤ xi < a and 1 ≤ yi < b. The positions of the coin and all the balls are mutually different.
The end of the input is indicated by a line consisting of five zeros. The number of datasets does not exceed 50. The sum of n of all the datasets does not exceed 5×105.
Output
For each dataset, output in a line all the ball numbers that you should strike to win the coin, separated by a single space. The ball numbers should be in ascending order. When there are no such balls, output "No" in one line.
Sample Input
6 6 4 4 4 2 2 3 3 5 5 5 1 4 5 2 2 1 3 3 4 5 1 4 3 1 2 3 4 3 2 0 0 0 0 0
Output for the Sample Input
2 4 1 No
Problem G
Two Sets of Cards
As an entertainment after the programming contest, you hold a game event for the participants.
Two sets of cards, red ones and blue ones, are used in the game. Both of the two sets have the same number of cards as the number of the participants, and each card has one integer written on it. It is known that the contents of these two sets are the same; the integers on the red cards are the same as those on the blue cards as multisets. Even though, you don't know what integers are actually written on the cards. The same integer may be written on two or more cards of the same color, and the integers may be negative.
You distributed one red card and one blue card to each of the participants. As the game result depends on the sum of the integers on the two cards distributed to each participant, you asked all the participants to declare their sums.
Your task is to find a possible card distribution consistent with the participants' declarations, that is, a combination of integers on the cards distributed to each participant. Note that such a combination might not exist, as the participants may commit miscalculations. In such a case, report that there is no consistent combination.
Input
The input consists of multiple datasets, each in the following format. The number of datasets does not exceed 100.
n
s1 s2 ⋯ sn
Here, n is the number of the participants, an integer between 1 and 70, inclusive. Each of si (i = 1, …, n) is the declared sum of the integers on the two cards distributed to the i-th participant, an integer between −150 and 150, inclusive.
The end of the input is indicated by a line consisting of a zero.
Output
For each dataset, if there exists no combination of integers on the cards distributed to each participant that is consistent with the participants' declarations, output "No" in one line. Otherwise, output "Yes" in one line followed by one possible consistent combination in the following format.
a1 a2 ⋯ an
b1 b2 ⋯ bn
Here, for i = 1, …, n, ai and bi represent the integers on the red and blue cards, respectively, distributed to the i-th participant. Each of ai and bi must be an integer between −109 and 109, inclusive. It can be proved that, when one or more consistent combinations exist, there also exists a consistent combination satisfying this condition. If there are two or more such combinations, you may output any one of them.
Sample Input
3 7 -2 3 3 4 8 8 4 1 2 4 8 6 -6 -2 3 2 9 -4 1 -100 0
Output for the Sample Input
Yes 1 -3 6 6 1 -3 Yes 2 4 4 2 4 4 No Yes 3 -1 4 -1 5 -9 -9 -1 -1 3 4 5 Yes -50 -50
Problem H
Blocking the Way
Alice is playing a puzzle game where she slides a tile piece to move it to its destination on a rectangular grid board consisting of unit squares. Only parallel moves of the piece on the game board are allowed; no rotations nor lifting up. Some squares on the board are marked no-entry where any parts of the tile piece should not enter.
The tile piece is composed of a number of unit squares joined tightly along their edges. The tile piece is initially placed to touch both the left and the top ends of the board. The goal of Alice is to slide the tile piece to make it touch both the right and the bottom ends of the board.
Bob, on the other hand, wants to make Alice's goal unachievable by changing some squares to no-entry. Each square, except for those initially covered by the tile piece, can be made no-entry by paying the specified number of coins. Compute the minimum number of coins Bob has to pay in total to make Alice's goal unachievable.
Input
The input consists of multiple datasets, each in the following format.
r c
a1,1 ⋯ a1,c
⋮
ar,1 ⋯ ar,c
Here, r and c are integers between 2 and 100, inclusive, representing the numbers of rows and columns of the board, respectively. The following ai,j (1 ≤ i ≤ r, 1 ≤ j ≤ c) are integers between −1 and 109, inclusive. Here, ai,j represents the state of the square (i, j) on row i and column j, as follows.
- If ai,j = −1, the square is initially covered by the tile piece.
- If ai,j = 0, the square is no-entry from the beginning.
- If ai,j > 0, Bob can make the square no-entry by paying ai,j coins.
It is guaranteed that, in the initial state, the tile piece is placed so that some of its edges touch the left end of the board and some touch the top end. It is also guaranteed that Alice has not yet achieved her goal. That is, the following two conditions are satisfied.
- There exists at least one i satisfying ai,1 = −1 and at least one j satisfying a1,j = −1.
- ai,c ≠ −1 for all i or ar,j ≠ −1 for all j.
The end of the input is indicated by a line consisting of two zeros. The number of datasets does not exceed 50. The sum of r of all the datasets does not exceed 1000. The sum of c of all the datasets does not exceed 1000. The total number of (i, j) satisfying ai,j = −1 of all the datasets does not exceed 1000.
Output
For each dataset, output on a single line the minimum number of coins Bob has to pay.
Sample Input
3 3 -1 33 22 99 0 99 11 44 99 4 3 -1 90 10 -1 90 20 20 50 99 10 20 99 3 3 -1 33 22 99 99 99 11 44 0 3 4 99 -1 10 99 -1 -1 -1 99 99 -1 99 99 0 0
Output for the Sample Input
33 40 0 10
Problem I
All Survived?
You are playing a first-person shooter with your friends. In this game, n players are divided into two teams fighting against each other. Each player is crowned with a balloon on top of the head, and players try to pop the balloons of the players of the opposing team.
Players are numbered from 1 through n, which are called the action orders. Also, each player is given a real number called the hit probability. The game consists of n phases. In the i-th (i = 1, …, n) phase, the player of the action order i (the attacker) takes the following action.
The game ends when all of the phases are completed.
You don't want any of the players of your team to be killed. Calculate the probability of keeping all the players of your team alive until the end of the game by optimally choosing the targets. Assume that the opposing players choose their targets at random.
Input
The input consists of multiple datasets, each in the following format. The number of datasets does not exceed 50.
n
s1 p1
⋮
sn pn
The integer n is the number of the players between 2 and 300, inclusive. For each i = 1, …, n, si and pi represent the team and the hit probability of the player of action order i, respectively. si is a string either of "Ally" or "Enemy", which means that the player belongs to your team or the opposite, respectively. pi is a real number between 0 and 1, inclusive, with 9 digits after the decimal point. It is guaranteed that both teams have at least one player.
The end of the input is indicated by a line consisting of a zero.
Output
For each dataset, output in a line the probability of keeping all the players of your team alive when targets are optimally selected. The absolute or relative error must be less than or equal to 10−9.
Sample Input
3 Ally 0.800000000 Enemy 0.300000000 Enemy 0.600000000 2 Enemy 0.444444444 Ally 0.111111111 5 Ally 0.500000000 Ally 0.750000000 Enemy 0.400000000 Enemy 0.100000000 Enemy 0.800000000 6 Ally 0.250000000 Ally 0.300000000 Enemy 0.200000000 Ally 0.800000000 Enemy 1.000000000 Enemy 0.750000000 10 Enemy 0.032876598 Ally 0.273941411 Ally 0.560821701 Ally 0.798896750 Enemy 0.559524781 Enemy 0.627232231 Enemy 0.864686751 Ally 0.991458997 Enemy 0.699768375 Enemy 0.675523871 0
Output for the Sample Input
0.616000000000 0.555555556000 0.621000000000 0.419750000000 0.142319776535
