百ます計算は計算練習の一種である． 百ます計算では 10 × 10 の空きマスがある紙を用いる． 各列の上端には 0 から 9 までの数が順不同に書いてあり， 各行の左端にも 0 から 9 までの数が順不同に書いてある． 空きマスには下図の例のように上端と左端の数の和を書き込んでいく．

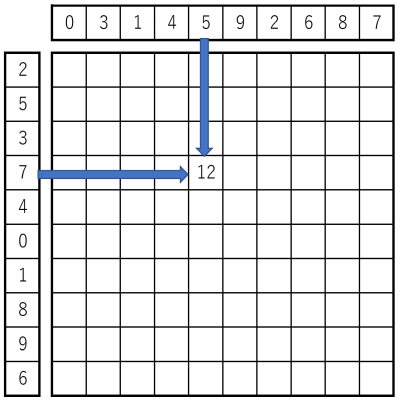
より一般化した問題を考えることもできる． そのような問題では，列や行の数を例えば w × h に変えることができる． また，各列の上と各行の左に書かれた数は，任意の整数とすることもできる．

英男君は，この一般化した百ます計算を題材にしてパズルを作っている． そのパズルでは，解答マスのいくつかに数が入っているが， 上端や左端の数は書いていない． パズルは解答マスに入っている数に矛盾しない上端・左端の数を見つける，というものだ．

英男君は解答マスがすべて正しい和で埋まっている紙を用意して， その解答マスの中の和をいくつか消していくことでパズル問題を作ることにした． こうすればパズルの解は少なくとも 1 つ存在することが保証できる． しかし解は存在するだけでは不十分で，一意であるようにしたい．

いろいろとやってみると，上端の数の一番左を 0 と決めておくとき， 横 w × 縦 h の解答マスのうち， w + h − 1 個のマスの値を残すと， 解が一意になることがあることがわかった． しかし，どのマスを残せば一意になるかはわかっていない．

英男君が作ったパズル候補のそれぞれについて， 解が一意に定まるかどうかを判定するプログラムを作って英男君を助けてあげて欲しい．

入力は 100 個以下のデータセットからなる． 各データセットは次の形式で表される．

w h
x₁ y₁ n₁
...
x_k y_k n_k

1 行目の w は横方向，h は縦方向の解答マスの個数である (2 ≤ w ≤ 100 および 2 ≤ h ≤ 100)． 解答マスには k 個 (k = w + h − 1) の数が残されている． 2 行目からの k 行は， 左から x_i 番目，上から y_i 番目の解答マスに n_i が入っていることを表す． x_i, y_i, n_i は，それぞれ 1 ≤ x_i ≤ w, 1 ≤ y_i ≤ h, −100 ≤ n_i ≤ 100 を満たす整数である． ここで，x_i = 1 が最も左，y_i = 1 が最も上のマスである． 異なる i と j について，x_i = x_j かつ y_i = y_j であることはない．

入力の終わりは，空白で区切られた 2 つのゼロからなる行で表される．

各データセットについて，パズルの解が一意に決まるならば YES，そうでなければ NO を 1 行に出力せよ．

2 2
1 1 10
1 2 1
2 2 5
3 3
1 1 1
1 2 2
2 2 3
2 3 4
3 3 5
3 3
1 1 1
1 3 3
2 2 3
3 1 3
3 3 5
3 2
1 1 8
1 2 7
2 1 7
3 2 5
6 6
1 1 -2
1 4 4
2 2 2
3 3 3
3 4 8
4 2 -4
4 6 1
5 5 4
5 6 5
6 1 -7
6 3 -6
6 6
1 2 3
1 4 0
2 1 -3
2 3 -1
3 1 0
3 2 6
4 6 0
5 4 -5
5 5 -10
6 3 -6
6 5 -10
6 6
1 5 -2
2 5 -1
3 5 -7
4 1 5
4 2 -1
4 3 4
4 4 3
4 5 -1
4 6 2
5 5 -6
6 5 0
2 6
1 1 -2
1 2 -1
1 3 -3
1 4 -2
1 5 -5
1 6 -2
2 4 0
0 0

YES
YES
NO
YES
NO
NO
YES
YES