私はちょうど敵国の ICPC 城の内部で任務を済ませたところだ． この後はあらかじめ地下に掘っておいた脱出路から退散する算段だ． ただ，城内には n 棟の物見やぐらが等間隔に設置されており， 物見やぐらの見張りに気づかれないように脱出路の入口まで移動しなければならない．

ICPC 城の敷地は 100n × 100 の長方形の形状をしている． ここで，左奥角の座標を (0, 0)，右手前角の座標を (100n, 100) としよう． 物見やぐらは 1 から n まで番号づけられており， k 番目の物見やぐらは座標 (100k − 50, 50) にある．

私の現在位置は座標 (x₁, y₁) であり， ここから敷地の中を移動しながら， 脱出路の入口がある (x₂, y₂) になるべく短い時間で到達したいと思っている．

物見やぐらの近くで高速に移動すると見張りが足音に気づいてしまう． 厳密には，最も近い物見やぐらまでの直線距離を D としたとき， 秒速 D² 以下で動かなければならない．

私は脱出路の入口まで最短何秒で移動できるだろうか．

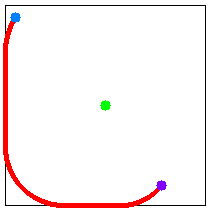
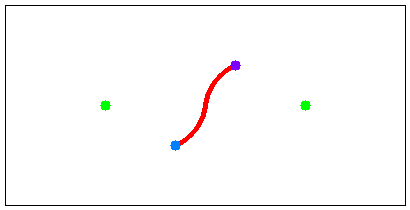
例えば物見やぐらが 1 棟で，移動の開始地点（現在位置）と終了地点（脱出路の入口）の座標がそれぞれ (5, 6) と (78, 90) のとき，図 H-1 の経路をたどれば最も早く脱出できる． また，物見やぐらが 2 棟で，移動の開始地点と終了地点の座標がそれぞれ (85, 70) と (115, 30) のとき，図 H-2 の経路をたどれば最も早く脱出できる． これらは Sample Input の最初の 2 つのデータセットに対応している．

図 H-1: 1 つめのデータセットにおける最適な移動経路	図 H-2: 2 つめのデータセットにおける最適な移動経路

入力は複数のデータセットからなる． 各データセットは次の形式で表される．

n x₁ y₁ x₂ y₂

n は物見やぐらの数を表す． n は正の整数であり，10⁷を超えない． (x₁, y₁) は移動の開始地点を表す． (x₂, y₂) は移動の終了地点を表す． x₁ と x₂ は，それぞれ整数であり，0 以上，100n 以下である． y₁ と y₂ は，それぞれ整数であり，0 以上，100 以下である． 移動の開始地点と終了地点の座標は異なる． また，移動の開始地点や終了地点の座標は，物見やぐらの座標とも一致しない．

入力の終わりは，5 つのゼロからなる行で表される． 入力に含まれるデータセットは 1000 個以下である．

各データセットについて，移動にかかる最短時間（秒）を出力せよ． 出力は相対誤差または絶対誤差が 10⁻⁸ 以下であれば許容される．

1 5 6 78 90
2 85 70 115 30
1 2 50 98 50
1 12 23 34 45
1 23 45 67 89
2 80 50 195 50
2 80 50 180 70
2 10 50 190 60
10 1 2 987 65
10 80 60 920 40
10 50 90 950 10
0 0 0 0 0

0.056924948365
0.024806946918
0.060137708723
0.039815727511
0.054616382922
0.070423053859
0.063218824369
0.091771006495
0.338081602957
0.297714980979
0.316557291903