Links
Problem D
Audience Queue
You are working as a staff member at a concert venue, organizing the audience queue. Everyone in the queue holds one ticket with a seat number printed. The seat numbers are integers from 1 to n without duplicates. Since this is a very popular concert, all the seats are reserved and exactly n people are in a single line.

Figure D-1: An example of the audience queue (The first dataset in Sample Input)
Your job is to split the line at some points and navigate each of the sublines to a distinct entrance gate. The audience are so polite that the order in each of the sublines is kept. There are k entrance gates, and thus you can split the line into k or less sublines. Sublines may have widely varying lengths, but empty sublines are not allowed. In the example of the figure below, the original line [4 2 3 5 1] has been split into three sublines, [4 2], [3 5], and [1].
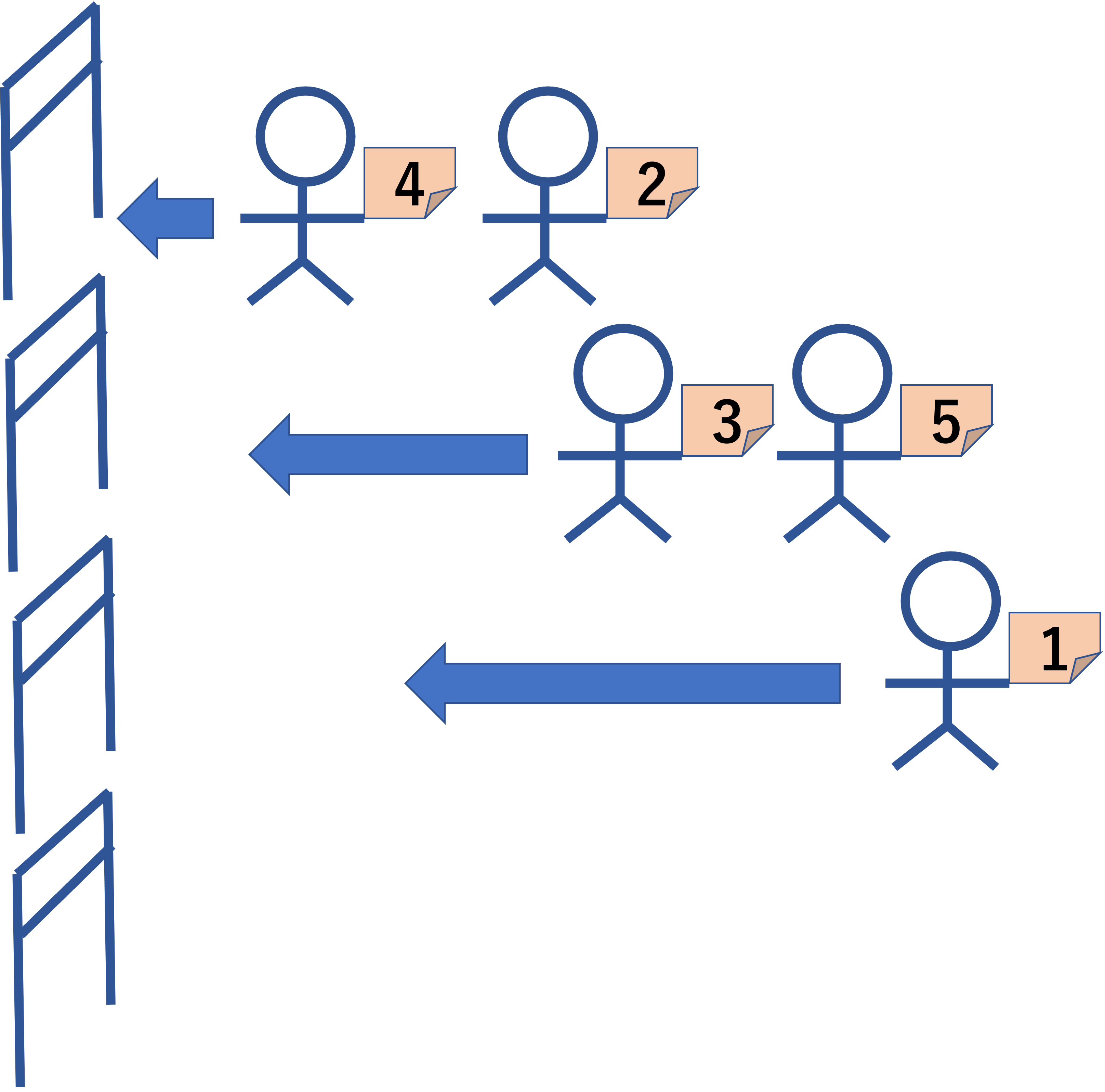
Figure D-2: An example of splitting the line
Although up to k lines are formed, the audience can enter the hall one at a time. Among those who head the lines, one with the smallest seat number enters the hall first. In the example figure below, among the heads 4, 3, and 1 of the lines, one with the smallest seat number, 1, enters the hall first. Subsequent entrance order is decided in the same way. Among those who head the lines at the time, one with the smallest seat number is the next to enter the hall.
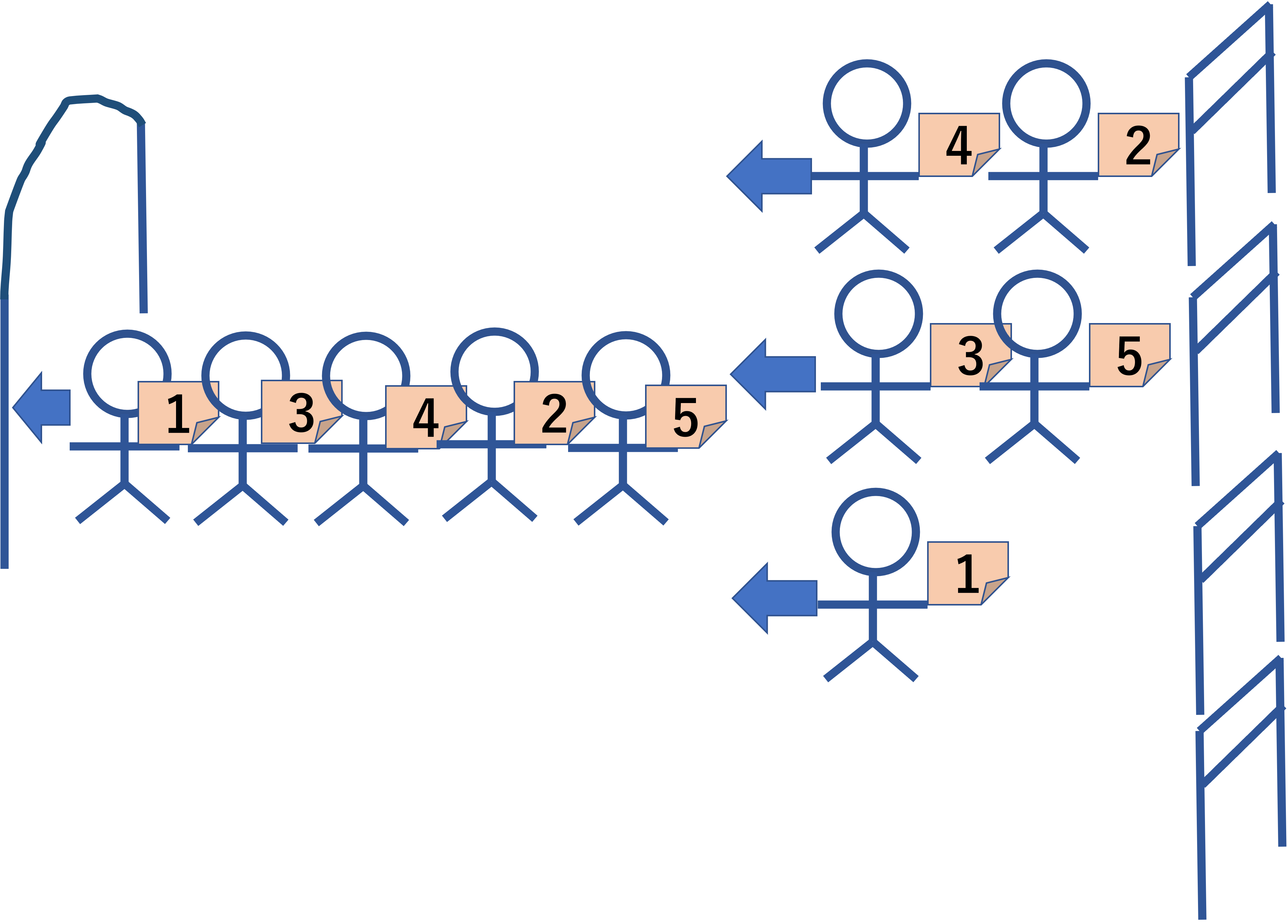
Figure D-3: An example of the order of the entrance
The order of entrance depends on how you split the audience line. Different ways of splitting may result in the same order. For the example above, splitting into [4 2], [3], [5], and [1] results in the same order.
Given the initial order in the queue and the final entrance order of the audience, please compute how many different ways of splitting the line result in the given final entrance order. For the same partitioning of the line, different assignments of sublines to gates are not counted separately.
Input
The input consists of multiple datasets, each in the following format.
n k
s1 ... sn
t1 ... tn
Integers n and k satisfies 1 ≤ k ≤ n ≤ 104. The number of the people in the audience line is represented by n, and the number of the gates is represented by k. The sequence s1 ... sn is a permutation of the integers 1 through n, which describes the initial order of the audience in the queue. The sequence t1 ... tn is also a permutation of the integers 1 through n, which describes the final entrance order.
The end of the input is indicated by a line "
Output
For each dataset, output in a line the number of ways to split the line as described in the problem statement.
Since the number can be very large, the output should be the number modulo the prime number
Sample Input
5 4 4 2 3 5 1 1 3 4 2 5 3 3 1 2 3 1 2 3 3 2 3 2 1 1 2 3 7 5 4 5 6 7 1 2 3 1 2 3 4 5 6 7 4 4 2 1 4 3 1 4 3 2 31 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 0
Output for the Sample Input
2 4 0 26 0 75497471
