acm International Collegiate Programming Contest

Links

A B C D E F G H

Problem G

Keep in Touch

Two agents A and B, known as a great combination, are conducting the infiltration mission to a secret base. Due to the strict security of the base, two agents have decided to follow the prechecked safe infiltration routes RA and RB, respectively. Each infiltration route is a two-dimensional polyline, a series of line segments.

Each of the agents starts at the starting end of the first segment of the corresponding route. The mission is over when both agents are on the finishing ends of the last segments of their routes simultaneously.

During the mission, each of the agents can move forward or backward at an arbitrary speed, or stop for a moment, as long as the movements along the route are continuous, but cannot jump changing the position abruptly. Although segments of a route may have crosses or overlaps with one another, they cannot be used for movements. Precisely, an agent on one segment can transfer to another segment only in the following cases.

  • The destination segment is the next segment on the route, and the agent is on the finishing end of the current segment.
  • The destination segment is the previous segment on the route, and the agent is on the starting end of the current segment.

For example, in Figure G-1 below, the agent must move to the finishing end of the segment 3-4 of RB, (−1, 1), in order to transfer to the segment 4-5. Although, the agent passes the same point as the finishing end of the last segment, (2, 1), when the agent transfers from the segment 2-3 to the segment 3-4, the agent is not considered to be on the finishing end of the last segment at that time.

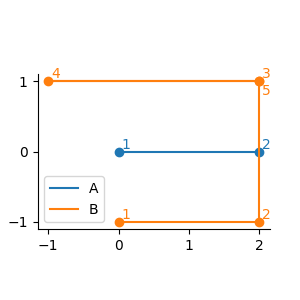
Figure G-1: Infiltration routes for the first dataset of Sample Input
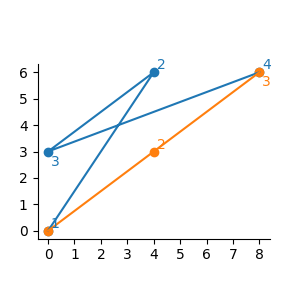
Figure G-2: Infiltration routes for the second dataset of Sample Input

To prepare for the contingency, the agents carry radio communicators and they should always be within the range allowing communication between them. Stronger wave enables longer communication distance, but increases the interception possibilities. Give the minimum required communication distance to accomplish the mission with appropriate movements of the agents.

Input

The input consists of multiple datasets, each in the following format.

n
xA,1 yA,1
 ⋮
xA,n yA,n
m
xB,1 yB,1
 ⋮
xB,m yB,m

n is the number of the vertices of the infiltration route RA. n is an integer between 2 and 40, inclusive.

xA,i and yA,i (1 ≤ i ≤ n) are the coordinates of the i-th vertex. xA,i and yA,i are integers satisfying −1000 ≤ xA,i ≤ 1000 and −1000 ≤ yA,i ≤ 1000, respectively. For 1 ≤ i ≤ n−1, (xA,i, yA,i) is the starting end of the i-th line segment, and (xA,i+1, yA,i+1) is its finishing end. All line segments have non-zero lengths. That is, xA,i ≠ xA,i+1 and/or yA,i ≠ yA,i+1 holds.

m and the value pairs of xB,j and yB,j (1 ≤ j ≤ m) represent the infiltration route RB. The format and the constraints are the same as those for RA.

The end of the input is indicated by a line containing a zero. The number of datasets does not exceed 50.

Output

For each dataset, output in a line the maximum distance between the two agents during the mission when they move in a way that minimizes the maximum distance. The error contained in the output should not exceed 10−8. The output shall be deemed correct if its relative error or its absolute error is within this limit.

Sample Input

2
0 0
2 0
5
0 -1
2 -1
2 1
-1 1
2 1
4
0 0
4 6
0 3
8 6
3
0 0
4 3
8 6
10
40 15
40 20
40 15
45 10
50 12
50 10
50 15
60 15
65 20
70 18
10
40 10
40 15
45 20
50 18
50 15
50 20
60 20
60 15
65 10
70 12
0

Output for the Sample Input

1.414213562373
2.400000000000
9.284766908853