Links
Problem D
入場待ちの行列
あなたはコンサート会場のスタッフとして聴衆の行列の整理にあたっている. 入場希望者は各自,座席番号の記されたチケットを一枚ずつ所持している. 座席番号は 1 から n までの整数で,重複はない. 人気のコンサートなので,座席は既に予約で満席になっており,ちょうど n 人が一列に並んでいる.

図 D-1: 入場列の例 (Sample Input の最初のデータセット)
あなたに任されている仕事は,この入場列を適当な何カ所かで区切って,それぞれの列を別々の入場ゲートに案内することである. 聴衆は皆礼儀正しいので区切られた列の中の順序が変わることはない. 入場ゲートは k カ所あるので,元の列を k 本以内の列に分割できる. 各列の長さは大きく異なっても良いが,空の列を作ってはならない. 下図の例では,元の列 [4 2 3 5 1] を 3 本の列 [4 2], [3 5], [1] に分割している.
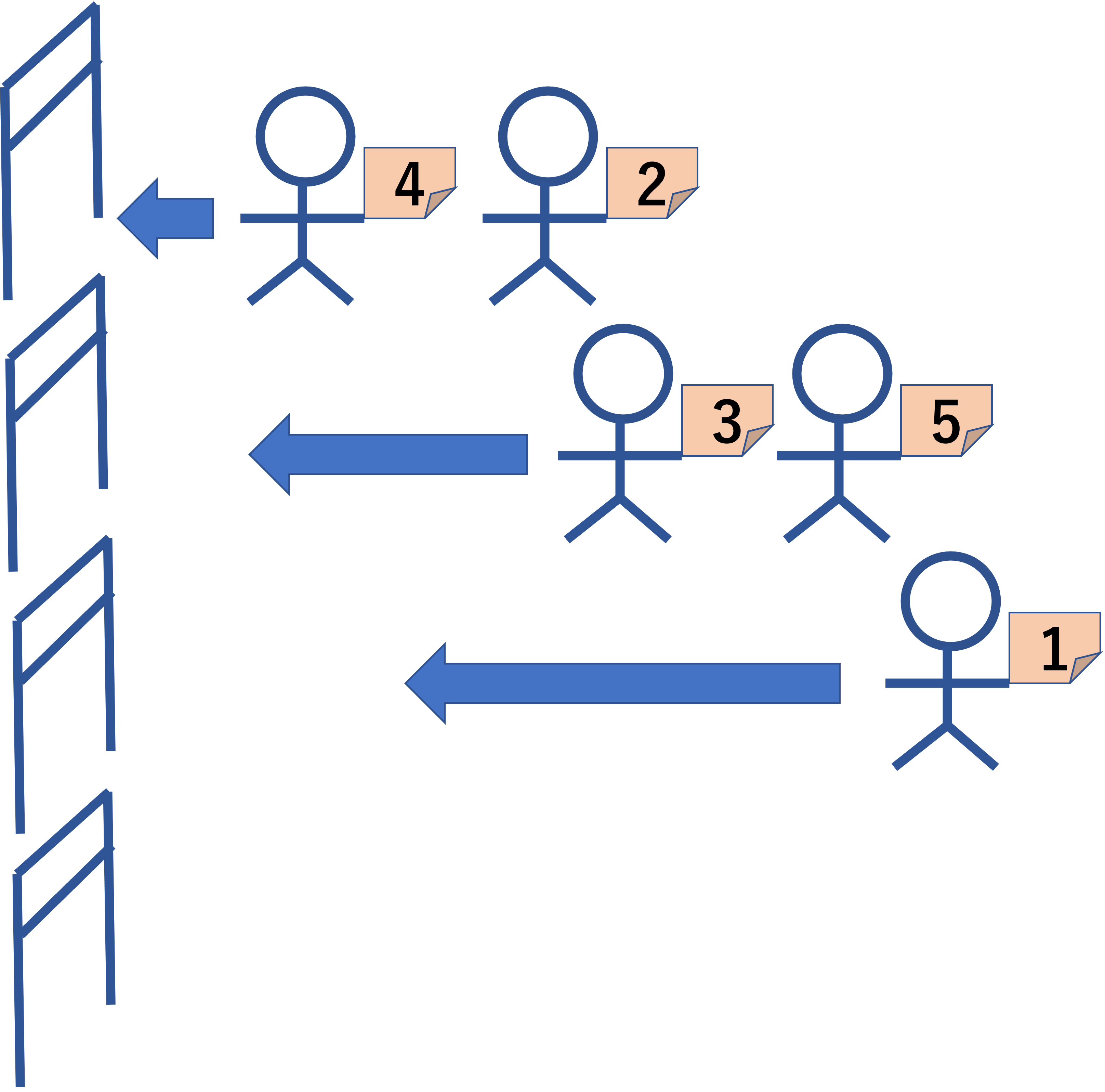
図 D-2: 列の分割の例
最大 k 本の列はできるが,聴衆は一人ずつしか会場に入っていけない. この際,各列の先頭のなかで,最も小さい座席番号の人が最初に入場する. 以下の図の例では先頭の 4, 3, 1 のうち最小の座席番号 1 番のチケットを持った人が最初に入場できる. その後の入場順も同様で,各列の先頭のなかで最も小さい座席番号の人が次の入場者となる.
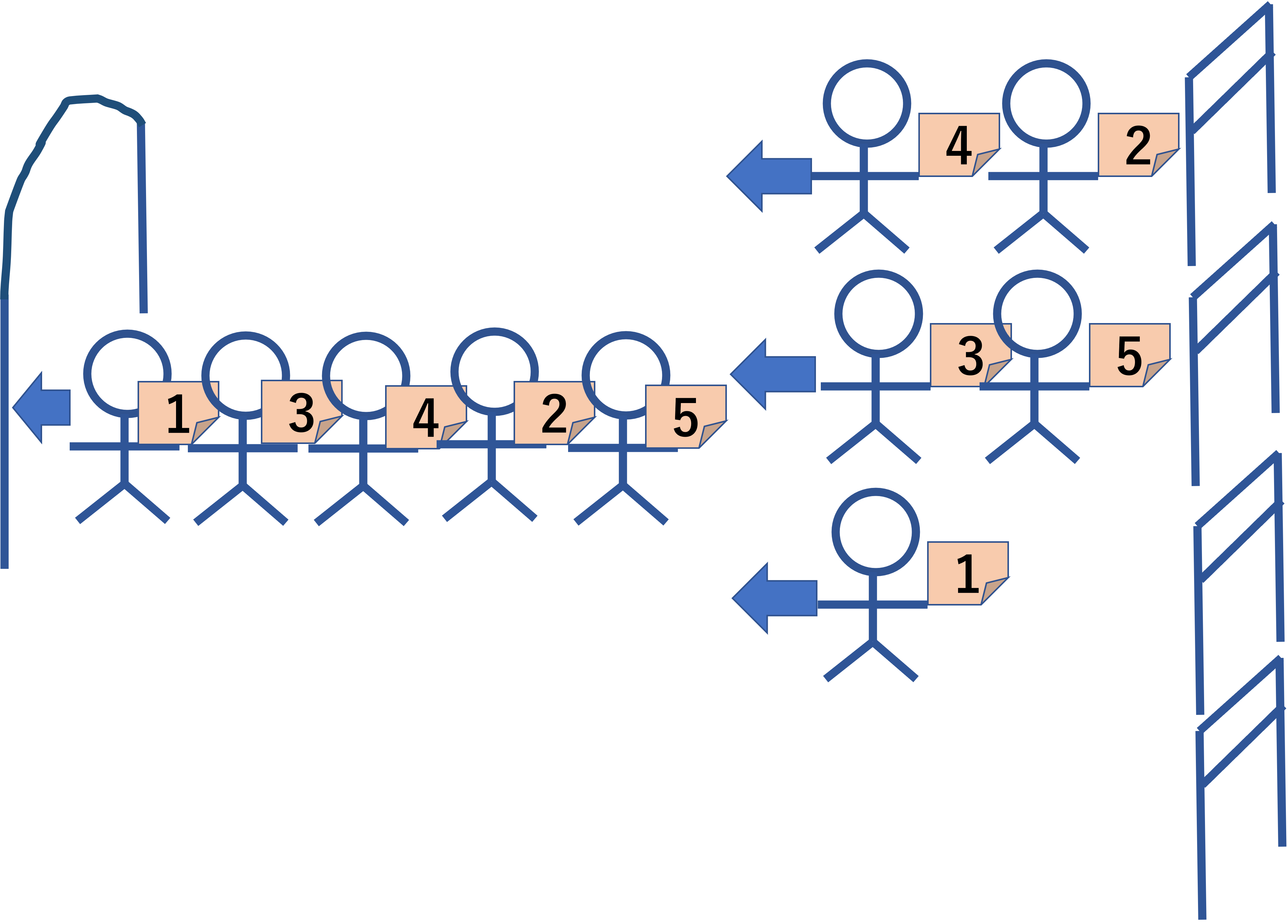
図 D-3: 入場の順の例
聴衆の列をどこで分割するかを決めると入場順が決まる. 異なる分割で同じ入場順になるかもしれない. 上の例では,[4 2], [3], [5], [1] と分割しても同じ入場順になる.
聴衆の最初の並び順と,実現したい最終的な入場順が与えられたとき,その入場順になるような列の分割の仕方が何通りあるか,計算してほしい. 分割の仕方が同じなら,どの列をどのゲートに案内するかは区別しない.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n k
s1 ... sn
t1 ... tn
整数 n, k は 1 ≤ k ≤ n ≤ 104 を満たし, n が列に並ぶ聴衆の人数を,k がゲートの数を表す. s1 ... sn は 1 から n までの整数を並べかえた列であり,聴衆の最初の並び順を表す. t1 ... tn も同様に 1 から n までの整数を並べかえた列であり,実現したい最終的な入場順を表す.
入力の終わりは,"
Output
各データセットについて,題意を満たす分割の仕方が何通りあるかを 1 行に出力せよ.
答えはとても大きくなり得るため,出力するのは素数
Sample Input
5 4 4 2 3 5 1 1 3 4 2 5 3 3 1 2 3 1 2 3 3 2 3 2 1 1 2 3 7 5 4 5 6 7 1 2 3 1 2 3 4 5 6 7 4 4 2 1 4 3 1 4 3 2 31 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 0
Output for the Sample Input
2 4 0 26 0 75497471
