The hundred-cell calculation is a kind of calculation training. In hundred-cell calculation, a sheet with ten by ten empty cells is given. Numbers, 0 through 9, are written on the top of the ten columns in an arbitrary order. 0 through 9 are also written at the left of the ten rows in an arbitrary order. You are to fill the empty cells with the sums of the top and left numbers, as an example shown in the figure below.

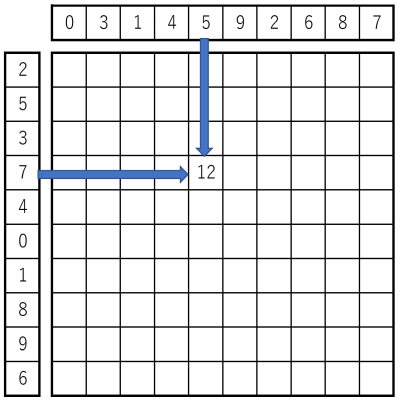
You may think of more generalized drills. Such a drill has different numbers of the columns and rows, say w × h. The numbers to be written on the top and the left can be any integers.

Hideo is designing a puzzle based on the generalized hundred-cell calculation. A sheet is given in which some of answer cells are filled with numbers, but numbers on the top and the left are omitted. The puzzle is to find these omitted numbers consistent with the filled numbers.

Hideo decided to construct puzzles by preparing sheets filled with all the correct sums and then removing some of these sums. This guarantees that the puzzle has at least one solution. The existence of the solution, however, is not enough; it should be unique.

Hideo has found through many trials that, when the leftmost of the numbers on the top is fixed to be 0, puzzles with w × h cells may have a unique solution when w + h − 1 sums are kept. He, however, could not figure out which cells to keep for a single unique solution.

Your task is to help Hideo by writing a program that judges solution uniqueness for each of the puzzle candidates he has made.

The input consists of at most 100 datasets, each in the following format.

w h
x₁ y₁ n₁
...
x_k y_k n_k

w and h in the first line are the numbers of answer cells in one row and in one column, respectively (2 ≤ w ≤ 100 and 2 ≤ h ≤ 100). There remain k numbers (k = w + h − 1) in the answer cells. The k lines starting from the second show that the number n_i is in the cell x_i-th from the left and y_i-th from the top. x_i, y_i, n_i are integers satisfying 1 ≤ x_i ≤ w, 1 ≤ y_i ≤ h, and −100 ≤ n_i ≤ 100. Here, x = 1 means the leftmost and y = 1 means the topmost. Either of x_i ≠ x_j or y_i ≠ y_j holds for different i and j.

The end of the input is indicated by a line containing two zeros separated by a space.

For each dataset, output YES if the puzzle has a unique solution, and NO otherwise, in a line.

2 2
1 1 10
1 2 1
2 2 5
3 3
1 1 1
1 2 2
2 2 3
2 3 4
3 3 5
3 3
1 1 1
1 3 3
2 2 3
3 1 3
3 3 5
3 2
1 1 8
1 2 7
2 1 7
3 2 5
6 6
1 1 -2
1 4 4
2 2 2
3 3 3
3 4 8
4 2 -4
4 6 1
5 5 4
5 6 5
6 1 -7
6 3 -6
6 6
1 2 3
1 4 0
2 1 -3
2 3 -1
3 1 0
3 2 6
4 6 0
5 4 -5
5 5 -10
6 3 -6
6 5 -10
6 6
1 5 -2
2 5 -1
3 5 -7
4 1 5
4 2 -1
4 3 4
4 4 3
4 5 -1
4 6 2
5 5 -6
6 5 0
2 6
1 1 -2
1 2 -1
1 3 -3
1 4 -2
1 5 -5
1 6 -2
2 4 0
0 0

YES
YES
NO
YES
NO
NO
YES
YES