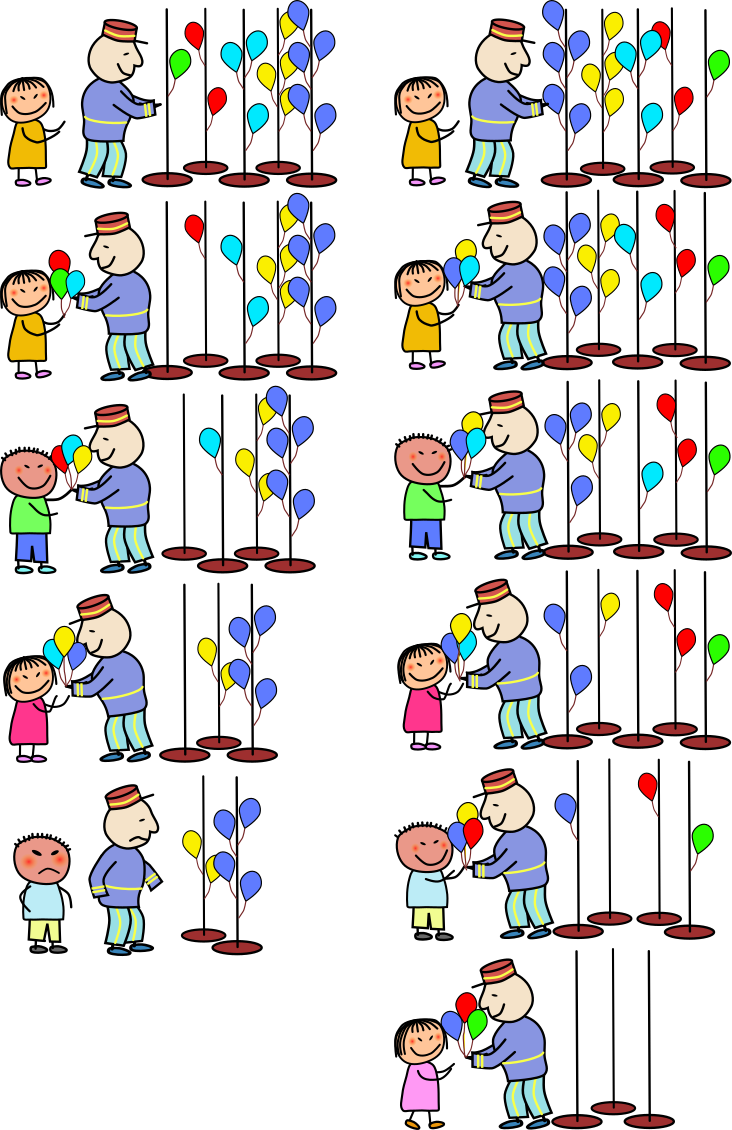
Each time an ICPC participant team has successfully solved a problem at the competition site, a balloon of a color specific to that problem is delivered to that team. You had thus prepared enough number of balloons of various colors for the case when all the teams solved all the problems, but many problems have been solved by few teams. You thus decided to give away the remaining balloons to the kids in the neighborhood.

You are preparing poles, each tied down with one or more balloons of the same color. You are lining up these poles from left to right. Whenever a kid comes up, you give three balloons of different colors to the kid picking up one from each of the three leftmost poles. Poles that run out of the balloons are removed, and when the poles remaining are two or less, you finish giving balloons away.

The number of kids you can give the balloons depends on the order of the poles. Find the maximum possible number of kids you can give the balloons by arranging the order of poles appropriately.

The figure on the right depicts the consequences of different arrangements of five poles with 1, 2, 3, 4 and 5 balloons. When poles are lined up in the order of 1, 2, 3, 4 and 5 balloons, you can give to only three kids; when they are in the order of 5, 4, 3, 2 and 1 balloons, you can give to five kids.

The input consists of multiple datasets, each in the following format.

n
b₁ b₂ … b_n

n is the number of poles. n is an integer between 3 and 50, inclusive. b₁ through b_n are the numbers of the balloons on the poles. Each b_i is a positive integer not exceeding 50.

The end of the input is indicated by a line containing a zero. The number of datasets does not exceed 50.

For each dataset, output a single line containing the maximum number of kids you can give the balloons to.

5
1 2 3 4 5
9
1 3 3 3 3 3 3 4 4
4
5 2 8 3
0

5
9
5