I've just completed a mission inside ICPC Castle in the enemy country, and am leaving the castle through the underground escape route dug in advance. However, there are n watchtowers placed at equal intervals in the castle, and I must reach the entrance of the escape route without being noticed by the guards in the watchtowers.

The yard of the castle has a rectangular shape of 100n × 100. Let the coordinates of the back left corner be (0, 0) and the coordinates of the front right corner be (100n, 100). The watchtowers are numbered from 1 to n, and the k-th watchtower is located at the coordinates (100k − 50, 50).

I am currently at the coordinates (x₁, y₁), and I want to move to the coordinates (x₂, y₂), where the entrance of the escape route is located, in the shortest possible time.

Should I move too fast near a watchtower, the guards might notice the footsteps. Strictly saying, I must not move faster than D² per second, where D is the distance to the nearest watchtower.

I'm wondering how long it takes to reach the entrance of the escape route.

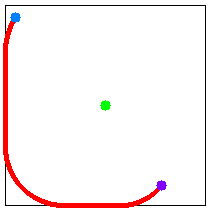
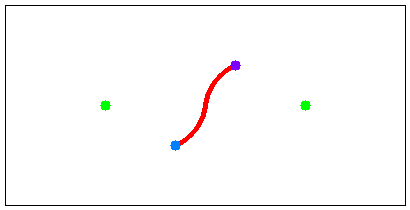
For example, when there is one watchtower and the coordinates of the starting location (current location) and the goal location (the entrance of the escape route) are (5, 6) and (78, 90), respectively, the optimal route is as shown in Figure H-1. For another example, when there are two watchtowers and the coordinates of the starting location and the goal location are (85, 70) and (115, 30), respectively, the optimal route is as shown in Figure H-2. These are corresponding to the first two datasets in the Sample Input.

Figure H-1: The optimal route for the first dataset	Figure H-2: The optimal route for the second dataset

The input consists of multiple datasets, each in the following format.

n x₁ y₁ x₂ y₂

n is the number of watchtowers. n is a positive integer not exceeding 10⁷. (x₁, y₁) gives the coordinates of the starting location, and (x₂, y₂) gives the coordinates of the goal location. x₁ and x₂ are integers between 0 and 100n, inclusive. y₁ and y₂ are integers between 0 and 100, inclusive. The coordinates of the starting and goal locations are different. The coordinates of the starting and goal locations are also different from those of any watchtowers.

The end of the input is indicated by a line containing five zeros. The number of datasets in the input is at most 1000.

For each dataset, output the shortest possible time to move in seconds. The error contained in the output should not exceed 10⁻⁸. The output shall be deemed correct if its relative error or its absolute error is within this limit.

1 5 6 78 90
2 85 70 115 30
1 2 50 98 50
1 12 23 34 45
1 23 45 67 89
2 80 50 195 50
2 80 50 180 70
2 10 50 190 60
10 1 2 987 65
10 80 60 920 40
10 50 90 950 10
0 0 0 0 0

0.056924948365
0.024806946918
0.060137708723
0.039815727511
0.054616382922
0.070423053859
0.063218824369
0.091771006495
0.338081602957
0.297714980979
0.316557291903