You are given a map of a dungeon consisting of a number of aligned squares forming a rectangle. Each square is either a wall or an empty square. The dungeon has no open space. More specifically, it satisfies the following two conditions.

1. No block of 2 × 2 or larger empty squares is in the dungeon.
2. Three or more empty squares are not diagonally aligned consecutively.

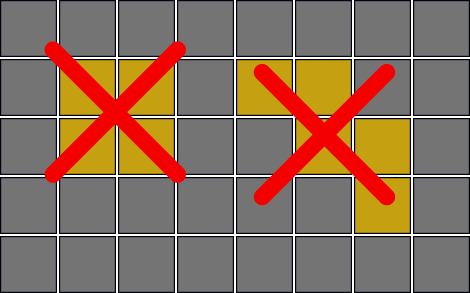
You have many lights. When you place a light on an empty square, it brightens that square and all the consecutive empty squares, if any, in the four directions, up, down, left and right. You can place at most one light in each empty square, and you can place the lights in as many squares as you want.

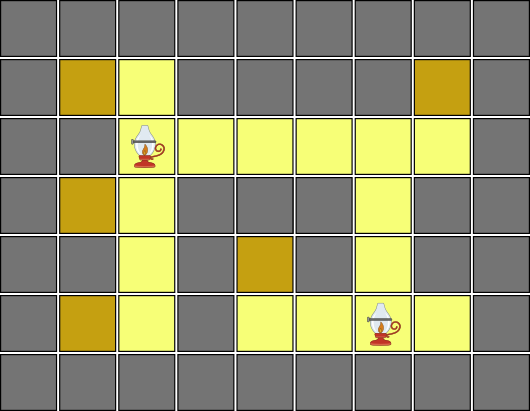
Compute the number of possible combinations of light placements that brighten all the empty squares.

The input consists of multiple datasets, each in the following format.

n m
c_1,1 ... c_1,m
...
c_n,1 ... c_n,m

n and m represent the number of squares in the vertical and horizontal directions, respectively, and satisfy 1 ≤ n ≤ 30 and 1 ≤ m ≤ 30. Each of c_i,j is a character '#' or '.'. If it is '#', the square at the position i from the top and j from the left is a wall; if it is '.', the square is empty.

The end of the input is indicated by a line containing two zeros. The number of datasets does not exceed 50.

For each dataset, output the number of possible combinations of light placements that brighten all the empty squares, modulo 10⁹+7 in a single line.

2 2
.#
#.
3 3
...
.#.
...
2 3
#..
..#
3 3
#.#
...
#.#
3 5
.#.#.
.....
#.#.#
0 0

1
161
9
25
243